| Basic Research | https://doi.org/10.21041/ra.v13i1.611 |
Sistema incorporado baseado em regras aplicado à determinação da saúde estrutural em edifícios multiníveis
Rule-based embedded system applied to determine the structural health of multilevel buildings
Sistema embebido basado en reglas aplicado a la determinación de la salud estructural en edificios de varios niveles.
F.
Ramírez-Cervantes1
* ![]() ,
F.
García-Lamont1
,
F.
García-Lamont1 ![]() ,
D. G.
Maxinez2
,
D. G.
Maxinez2 ![]() ,
J.
Ayala1
,
J.
Ayala1 ![]() ,
R.
García3
,
R.
García3 ![]()
1 CU-UAEM Texcoco, Universidad Autónoma del Estado de México, Texcoco, Estado de México, México.
2 FES Aragón, Universidad Nacional Autónoma de México, Nezahualcóyotl, Estado de México, México.
3 CU-UAEM Ecatepec, Universidad Autónoma del Estado de México, Ecatepec, Estado de México, México.
*Contact author: framirezc@uaemex.mx
Recepção:
22
de
maio
de
2022.
Aceitação:
13
de
dezembro
de
2022.
Publicação: 01 de janeiro de 2023.
| Citar como:Ramírez-Cervantes, F., García-Lamont, F., Maxinez, D. G., Ayala, J., García, R. (2023),“Sistema incorporado baseado em regras aplicado à determinação da saúde estrutural de edifícios com vários andares”, Revista ALCONPAT, 13 (1), pp. 28 –44, DOI: https://doi.org/10.21041/ra.v13i1.611 |
Resumo
O objectivo do trabalho era desenvolver um sistema baseado em regras para apoiar a determinação da saúde estrutural de edifícios de vários andares. As técnicas de descrição de hardware são utilizadas através de lógica programável usando integração de entidades e desenho hierárquico com programação VHDL. O sistema está incorporado numa FPGA que, através de um algoritmo, integra uma primeira fase em que um grupo de sensores de ultra-sons recolhe uma medição que é interpretada para obter o deslocamento relativo do mezanino. Na segunda fase, um motor de inferência realiza a avaliação. Apresentamos resultados utilizando um modelo experimental onde foi verificado que o sistema foi capaz de determinar a estabilidade da estrutura com base no parâmetro de deslocamento relativo.
Palavras chave:
monitorização da saúde estrutural,
deslocamento relativo,
lógica programável,
sistema baseado em regras.
1. IntroduÇÃo
O SHM Structural Health Monitoring de monitoramento de integridade estrutural com base na tecnologia de sensores foi aceito como um método importante para avaliações de segurança de estruturas de engenharia. Em SHM, as respostas de uma estrutura são tradicionalmente medidas usando várias tecnologias, como acelerômetros (Arias e De la Colina, 2018), sensores de fibra óptica distribuídos (Bao e Chen, 2012), sensores de deslocamento a laser LDS, Laser Displacement Sensor, por sua sigla em inglês (Song et. al., 2006; Park et. al., 2013), sistema de posicionamento global GPS, Global Positioning System, por sua sigla em inglês, (Tamura et. al., 2002; Breuer et. al. , 2002) e transdutores de deslocamento variável linear LVDT, transdutores de deslocamento variável linear, (Arias e De la Colina, 2018), sensores sem fio (Li et. al., 2019; Guo et. al. ., 2014; Zrelli e Ezzedine, 2017 ) e circuito da ponte de Wheatstone (Li e Hao, 2016). Da mesma forma, para esse fim, várias técnicas de processamento e avaliação de dados foram usadas, como aprendizado profundo (Li et. al., 2019; Guo et. al., 2014), otimização de grupos de partículas PSO, otimização de partículas (Chatterjee et. al., 2017; Moosazade et. al., 2019) e algoritmos genéticos (Ghasemi et. al., 2018). Por fim, os dados são transferidos para um servidor de monitoramento para análise das informações históricas registradas e avaliação por especialistas da área. As características da estrutura e as várias cargas (carga de vento, carga sísmica e carga de serviço) determinam os elementos estruturais alvo, tipos de resposta e sensores de medição necessários. Portanto, a seleção de um índice de resposta que possa avaliar com precisão os danos a uma estrutura é fundamental.
Para o desenvolvimento de aplicações no nível da microeletrônica, é utilizada uma metodologia de projeto de circuitos integrados para aplicações específicas ASICs, Application-Specific Integrated Circuits, que apresenta diversas alternativas de desenvolvimento (Maxinez e Alcalá, 2007). Lógica programável é um tipo de projeto que através do uso de dispositivos lógicos programáveis PLDs, Dispositivos Lógicos Programáveis, como FPGAs, Field Programmable Gate Arrays, que podem ser caracterizados externamente por várias programações técnicas usando uma linguagem de descrição de hardware HDL, Hardware Description Language.
O objetivo deste trabalho é apresentar uma proposta de desenvolvimento de um sistema eletrônico capaz de determinar a estabilidade de um edifício de vários pavimentos a partir da avaliação da medição do deslocamento relativo do mezanino que é obtido por uma rede de sensores ultrassônicos e que adquirem medidas diretamente dos elementos estruturais verticais de forma não invasiva.
2. Desenvolvimento metodológico
Nesta secção apresentamos o desenvolvimento da nossa proposta, primeiro propomos as especificações e os cenários, para depois começar com a modelação da proposta, continuando com a abordagem dos algoritmos de solução e sua programação, terminando com a implementação do sistema.
2.1 Especificações e cenários
O parâmetro mais importante para determinar a magnitude de possíveis danos às edificações é a distorção do pavimento γ, ou seja, o deslocamento relativo do pavimento ∆, dividido pela altura do pavimento H.

Na equação (1) pode-se observar que a distorção do pavimento é um parâmetro adimensional, pois tanto Δ quanto H possuem dimensões de comprimento, podendo ser utilizado em termos percentuais. Para avaliar nos baseamos no que foi estabelecido por Paulay, (2001) a qual propõe que a medida de deslocamento médio admissível ficará entre 2,0 e 2,5% de H, a partir desta premissa será construída a tabela do motor de inferência do sistema e a partir desta o sistema irá reagir de uma forma predeterminada para acionar os atuadores planejados.
O caso prático não é um caso geral, é especificamente proposto para uma estrutura com geometria retangular bem definida, para a qual é utilizado o modelo de uma estrutura de seis níveis com altura de cada pavimento H i = 3,5 m, com vértices flexíveis em cada nível, para a geração de inclinações. O objetivo do modelo utilizado é apenas a coleta de medidas para obter o deslocamento relativo da história e as tensões analisadas são de natureza unidimensional, pois, caso contrário, uma geometria geral teria que ser analisada com tensões de uma natureza vetorial que podem causar deslocamentos em mais de uma direção, induzir rotações, modos de vibração transversais, longitudinais, torcionais, etc. Portanto, é importante mencionar que a análise é limitada à tensão unidimensional na estrutura retangular livre de vibração.
Para obter o valor do estado limite inferior do caso proposto, utilizamos a equação (1) e a formulamos da seguinte forma:
 |
Devemos considerar que 2,0% de Hi é 0,07m. Assim, para o caso, obtemos:

Para obter o deslocamento médio máximo admissível da estrutura completa, utiliza-se o deslocamento médio multiplicado pelo número de níveis, neste caso obtém-se o deslocamento relativo do limite inferior entre andares:
Da mesma forma, para obter o valor do estado limite superior, devemos considerar que 2,5% de Hi é 0,0875m. E obtemos:
2.2 Modelagem
Numa primeira fase, para obter a medição do deslocamento relativo do mezanino de uma estrutura modelo de seis andares, propõe-se desenvolver o bloco Sistema de Sensor de Deslocamento Relativo Ultrassônico em Pêndulo (SSDRUP), no qual a medição do deslocamento relativo do pavimento é calculado, para isso, foi projetado um sistema que integra uma rede de sensores ultrassônicos de alta capacidade HC-SR04 colocados suspensos no teto do pavimento para obter a medição do deslocamento relativo em pontos específicos de um edifício, os sensores são os elementos capazes de obter o parâmetro de um sinal físico que é condicionado em um sinal conveniente para sua interpretação e, assim, integrá-los a um sistema de aquisição de dados para adaptar os sinais obtidos em dados que podemos processar na etapa de análise. A Figura 1 mostra os parâmetros a serem considerados: medição obtida pelo sensor M
i
, medição da base do triângulo semelhante que é gerado no triângulo do lado direito m
i
, deslocamento relativo do pavimento ∆
i
e a altura do pavimento H
i
, que é um fato conhecido. Quando a estrutura sofrer uma inclinação (deformação), os sensores para M
i
devido ao efeito da gravidade permanecerão no eixo vertical original das ordenadas, a parede do pavimento seguirá a inclinação do pavimento, assim, ao projetar a inclinação, devemos considerar que as referências dos eixos coordenados são traduzidas e que a referida projeção descreve dois triângulos, podemos identificar que ambos os triângulos contêm dois triângulos semelhantes que obedeceriam ao primeiro teorema de Tales, então, aplicando as relações de semelhança para triângulos semelhantes, podemos obter o valor de as bases, lembrando que a base do triângulo do lado direito, como a representamos no diagrama, identificamos como sendo o deslocamento relativo do andar ∆
i
. A medida M
i
obtida por cada sensor varia, sofrendo um decréscimo que será utilizado para que, através da relação de semelhança aplicável ao caso, se obtenha o comprimento da base do triângulo da direita, que, conforme indicado, corresponde ao deslocamento relativo do pavimento ∆
i
. Com esses dados, calcula-se a distorção do pavimento de cada nível e determina-se qual das medições é a maior para entrar na avaliação do estado limite.
Como já explicado, podemos nos basear no primeiro teorema de Tales e estabelecer uma relação para triângulos semelhantes:
Identificando os elementos temos que:
A medida AB = H
A medida B´C´= m
A medida m = X - M
A medida BC = ∆
Então, da equação (6), tiramos:
Substituindo temos:
Isolando ∆ obtemos a expressão:
Numa segunda fase, é recebido o valor da medição do deslocamento relativo do pavimento, cuja magnitude é a maior das seis que foram determinadas, este parâmetro será a variável de entrada para um sistema baseado em regras (SBR), a análise será ser feito com base nos princípios da lógica fuzzy para o qual primeiro atribuímos um universo de discurso no intervalo desejado, neste caso de 0cm a 70cm, onde 0cm representa o estado inicial e calibrado da perpendicular do edifício e sua base, e 70cm consideramos um valor suficientemente admissível pois pelos cálculos obtidos em (4) e (5) o estado limite para o caso é entre 42,0cm e 52,5cm com o qual determinamos fixar os limites entre 39,0cm e 53,0cm o que significa que uma medida superior a 53,0cm representaria que a estrutura estaria em perigo de desabamento, razão pela qual o alcance que propomos é mais do que suficiente para permitir que o sistema de inferência funcione em um intervalo maior que os limites estabelecidos e não atue imediatamente se essas medidas forem ultrapassadas.
Com essa consideração, decidimos usar quatro funções de pertinência: duas trapezoidais e duas triangulares, para dar significado a cada variável linguística. Cada função de pertinência identifica o intervalo de valores de entrada que correspondem a uma variável linguística, as funções de pertinência mapeiam os dados presentes para determinar o grau de pertinência. Ou seja, os valores físicos da variável de entrada que é a maior das medidas obtidas pelos sensores são convertidos em valores linguísticos.
Na Tabela 1 mostramos os intervalos como a variável de entrada é particionada (dividida), esses intervalos foram definidos subjetivamente com o apoio de um especialista, que ajustou esses intervalos para que o comportamento da medida de entrada observe a correta atribuição de pertinência à função na qual obteve o maior valor.
Aplicamos o que determinamos e alimentamos o software fuzzyTECH usando uma função de pertinência para cada faixa estabelecida, sendo duas triangulares e duas trapezoidais. Na Figura 2 podemos identificar as funções de pertinência para a variável de entrada DESP_REL que corresponde à maior das medidas de deslocamento relativo e que são definidas com os termos linguísticos: ESTÁVEL, REGULAR, LIMITE e PERIGO. As quatro funções de pertinência utilizadas permitem que os intervalos calculados para o caso prático de não acionem as saídas para os atuadores até atingir um limite máximo; ou seja, propor duas funções de pertinência triangular para os termos REGULAR e LIMITE permite manipular valores entre 32,0 cm e 53,0 cm para identificar o valor de pertinência de um valor físico da variável de entrada a fim de observar o comportamento desta e nesta faixa , é atribuído um grau de pertença que corresponde a uma variável linguística que nos permite dosar o funcionamento dos atuadores na fase seguinte.
Agora extraímos convenientemente os intervalos para cada função de pertinência, para descrever cada um deles usamos a equação da linha de inclinação do ponto e obtemos:


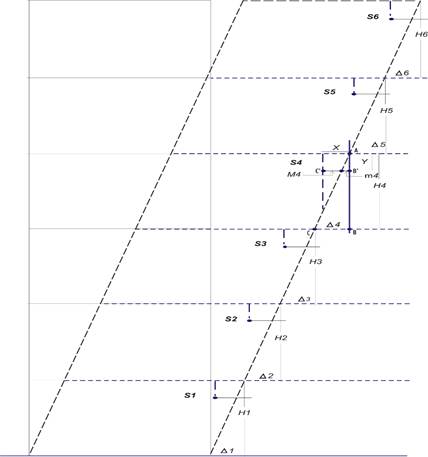
Figura 1.
Parâmetros para medição dos deslocamentos relativos entre pavimentos.




Tabela 1.
Intervalos da variável de entrada DESP_REL.
Conjunto
Intervalo (cm)
ESTÁVEL
0 - 39
REGULAR
32 - 46
LIMITE
39 - 53
PERIGO
46 - 70
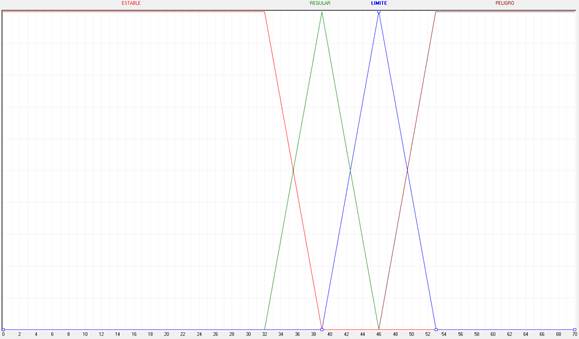
Figura 2.
Funções de pertinência da variável DESP_REL no intervalo [0-70].

Terceira etapa: Raciocínio. Este processo de inferência determina a saída mais apropriada do sistema a partir de duas implicações, por um lado, os dados de entrada e, por outro, a base de conhecimento. A inferência é uma computação que consiste em duas etapas principais: agregação e conclusão. Isso nos permitirá obter deduções lógicas de proposições. O conhecimento é apresentado por regras da forma IF- THEN, o comportamento real do sistema é definido nas regras individuais. Para criar um protótipo de um conjunto apropriado de regras, você começa criando regras que representam estratégias inequívocas do controlador em pontos operacionais específicos.
Uma vez estabelecidas estas, pode-se proceder à construção do conjunto de regras, na Tabela 2 apresentamos as quatro regras que foram estabelecidas como suficientes para determinar o comportamento desejado do sistema, isto foi feito por atribuição direta de comportamento aos atuadores que foi determinado com a ajuda do especialista.
| Tabela 2. Regras de produção. | ||||||||||||||
| DESP_REL | A_VISUAL | A_ACÚSTICO | A_MENSAGEM | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ESTÁVEL | AVVERDE | DESLIGA | DESLIGA | |||||||||||
| REGULAR | AVAMARELO | DESLIGA | AMCUIDADO | |||||||||||
| LIMITE | AVAMARELO | DESLIGA | AMALERTA | |||||||||||
| PERIGO | AVVERMELHO | ALERTA | AMALERTA | |||||||||||
Quarta etapa. Nesta fase, obtemos o valor exato da saída. Então só precisamos transformar os valores de pertinência entregues pelo motor de inferência, em um valor real para fins práticos a partir dos consequentes das regras que foram ativadas, é necessário obter uma única ação de controle, combinando o resultado proposto por cada um deles.
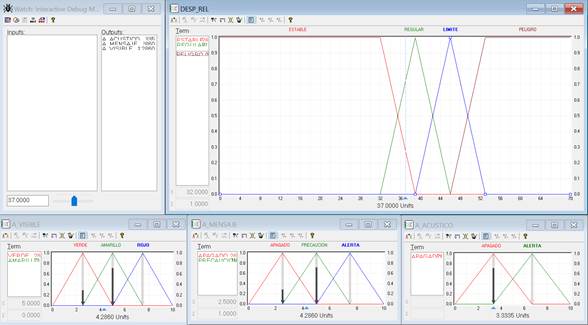
Uma verificação de sistema projetada é iniciada invocando um modo de depuração do software fuzzyTECH. Todas as alterações feitas no driver são implementadas imediatamente na tarefa atual do driver depurado, isso permite testar as alterações inseridas no driver devido a dados de entrada específicos, ou seja, verificar o comportamento do sistema com dados inseridos manualmente. A faixa de 0 cm a 70 cm é totalmente coberta, a Figura 3 mostra o caso quando a entrada é alimentada com um valor de 37 cm que é alimentado manualmente e o valor que corresponderia às saídas.
 |
||||
| Figura 3. Depuração do sistema projetado (entrada de 37 cm). | ||||
2.3 Algoritmo proposto
Assim, propomos proceder da seguinte forma:
Início Declaração do tipo de dados de inferência (estável, regular, limite, perigo) Processo de Pertinência Converter distância (BCD) para dis (inteiro); Avaliar dis Atribuir InclinaçãoNegativa e InclinaçãoPositiva Atribuir Negativo e Positivo Fim Avaliar Fim PERTINENCIA Processo RAZÃO Declaração de variáveis do processo enquanto InclinaçãoNegativa < InclinaçãoPositiva resultado = InclinaçãoPositiva e pertinencia = PertinenciaPositivo Se nenhum resultado = InclinaçãoNegativa e pertinencia = PertinenciaNegativo Fim Enquanto Fim RAZÃO Processo SAÍDA Se borda ascendente Avalie Pertinencia Atribuir valores às saídas Fim Avaliar Fim SAÍDA
Algoritmo SBR para SSDRUP.
2.4 Implementação
Uma vez depurado, verificado e otimizado o sistema, podemos programar os módulos necessários para implementar o Sistema Baseado em Regras para Sistema de Sensor de Deslocamento Relativo por Pêndulo Ultrassônico (SBR para SSDRUP).
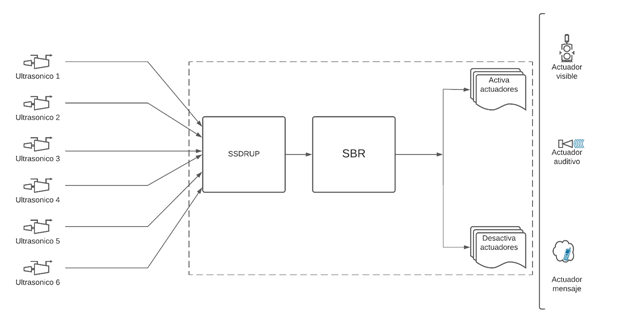
Em seguida, o SBR para SSDRUP incorpora o mecanismo de inferência que é responsável por realizar a avaliação de todas as medições coletadas pelos sensores, determina a maior das medições, avalia e estabelece o estado de integridade estrutural que é determinado com as regras de inferência e gera a lógica níveis das saídas do sistema para ativar ou não o funcionamento dos atuadores planejados. Finalmente, a Figura 4 mostra o sistema SBR completo para SSDRUP.
 |
||||
| Figura 4. Esquema geral do sistema. | ||||
3. Materiais e mÉtodos
Foi utilizado um modelo construído em madeira com vértices flexíveis para permitir que as inclinações sejam geradas de forma manual e independente para cada nível. Instrumentado com um sistema de seis sensores ultrassônicos HC-SR04, um em cada nível suspenso a 45cm do teto do mezanino e a uma distância de 50cm da parede limite localizada na entrada da força lateral, com a finalidade de suspender o sensor no teto do nível a analisar é gerar um efeito de pêndulo quando ocorre a inclinação (ver Figura 5). O sistema requer apenas uma calibração simples com o eixo de referência vertical. O sensor não girou durante a medição, a aproximação do pêndulo é para pequenas oscilações, o ângulo subtendido entre o emissor ultrassônico, o ponto de contato na estrutura e o receptor de eco é praticamente zero. O sensor manteve a vertical o tempo todo durante a medição, de forma que a estrutura é a que ficou oscilando, porém, no uso do pêndulo pode haver mudanças de fase que alterem a medição.
 |
||||
| Figura 5. Instrumentação do modelo com sensores HC-SR04. | ||||
Para a fase de modelagem e verificação contamos com o apoio do Engenheiro Civil Jesús Carrillo Sánchez da UNAM e foi utilizado o software fuzzyTECH 6.03 IA-S7, que permite a definição gráfica das funções de pertinência de cada termo utilizado e a depuração sistema projetado
O sistema projetado foi implementado utilizando uma metodologia de projeto hierárquico e integração de entidades lógicas programáveis e sua programação na linguagem de descrição de hardware VHDL na plataforma Intel Quartus II V.13.0.1 Web Edition. O SBR para SSDRUP foi embutido em um FPGA EP2C5T144C8 (ver Figura 6) e o condicionamento dos sinais de saída aos atuadores possui indicadores visuais dos níveis lógicos presentes.
 |
||||
| Figura 6. SBR para SSDRUP embutido no FPGA EP2C5T144C8. | ||||
4. Experimentos e resultados
Para validar o sistema implementado, instrumentou-se o modelo descrito e projetou-se um conjunto de testes onde em cada experimento cada um dos seis níveis do modelo utilizado é manipulado de forma independente de forma que em cada um deles são geradas diferentes inclinações, o SSDRUP obtém as medidas de deslocamento relativo de cada mezanino e determina a maior dessas medidas que SBR para SSDRUP entra para avaliação.
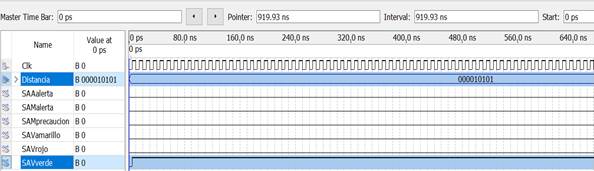
Teste 1. SSDRUP determinou 21cm como a maior das seis medidas com as quais SBR para SSDRUP atribui a pertinência da variável de entrada ao valor linguístico ESTÁVEL e estabelece os níveis lógicos para as saídas dos atuadores conforme podemos verificar na Figura 7.
 |
||||
| Figura 7. Diagrama de tempo do Teste 1. | ||||
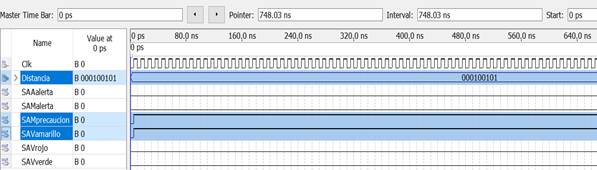
Teste 2. O SSDRUP determinou 37cm como a maior das seis medidas com as quais o SBR para SSDRUP atribui a pertinência da variável de entrada ao valor linguístico REGULAR, e estabelece os níveis lógicos para as saídas dos atuadores conforme podemos verificar na Figura 8.
 |
||||
| Figura 8. Diagrama de tempo do Teste 2. | ||||
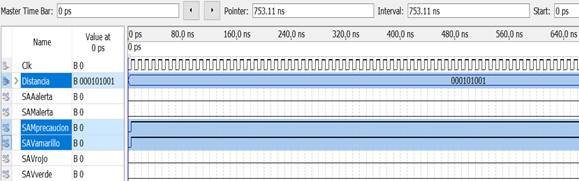
Teste 3. O SSDRUP determinou 41cm como a maior das seis medidas com as quais o SBR para SSDRUP atribui a pertinência da variável de entrada ao valor linguístico REGULAR e estabelece os níveis lógicos para as saídas dos atuadores conforme podemos verificar na Figura 9.
 |
||||
| Figura 9. Diagrama de tempo Teste 3. | ||||
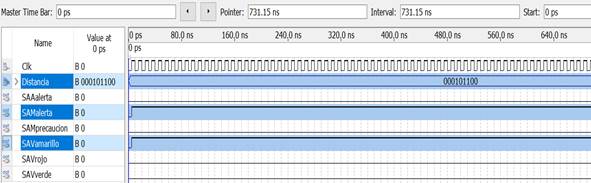
Teste 4. SSDRUP determinou 44cm como a maior das seis medidas com as quais SBR para SSDRUP atribui a pertinência da variável de entrada ao valor linguístico LIMITE e estabelece os níveis lógicos para as saídas dos atuadores conforme podemos verificar na Figura 10.
 |
||||
| Figura 10. Diagrama de tempo Teste 4. | ||||
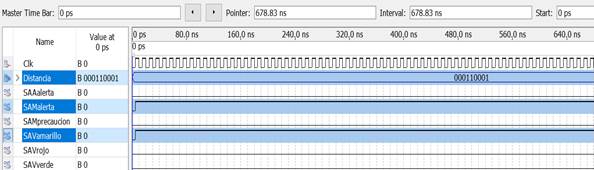
Teste 5. SSDRUP determinou 49cm como a maior das seis medidas com as quais SBR para SSDRUP atribui a pertinência da variável de entrada ao valor linguístico LIMITE e estabelece os níveis lógicos para as saídas dos atuadores conforme podemos verificar na Figura 11.
 |
||||
| Figura 11. Diagrama de tempo Teste 5. | ||||
Teste 6. O SSDRUP determinou 50cm como a maior das seis medidas com as quais o SBR para SSDRUP atribui a pertinencia da variável de entrada ao valor linguístico PERIGO e estabelece os níveis lógicos para as saídas dos atuadores conforme podemos verificar na Figura 12.
 |
||||
| Figura 12. Diagrama de tempo Teste 6. | ||||
Os valores lógicos presentes nas saídas para os atuadores são verificados fisicamente nos indicadores visuais das saídas condicionadas e são informados na Tabela 3:
| Tabela 3. Valores lógicos presentes nas saídas para os atuadores. | ||||||||||||||
| Teste | Δ(cm) | Pertence | SAAalerta | SAV verde | SAV amarelo | SAV vermelho | SAM cuidado | SAM alerta | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 21 | ESTÁVEL | 0 | 1 | 0 | 0 | 0 | 0 | ||||||
| 2 | 37 | REGULAR | 0 | 0 | 1 | 0 | 1 | 0 | ||||||
| 3 | 41 | REGULAR | 0 | 0 | 1 | 0 | 1 | 0 | ||||||
| 4 | 44 | LIMITE | 0 | 0 | 1 | 0 | 0 | 1 | ||||||
| 5 | 49 | LIMITE | 0 | 0 | 1 | 0 | 0 | 1 | ||||||
| 6 | 50 | PERIGO | 1 | 0 | 0 | 1 | 0 | 1 | ||||||
Teste 1: O sistema determina que a medida de deslocamento relativo de 21cm pertence a uma categoria determinada como ESTÁVEL, então aciona a saída para o atuador visual verde e mantém os demais atuadores desligados, indicando que a estrutura está estável e sem risco de colapso. Testes 2 e 3: Com medidas de 37cm e 41cm, respectivamente, o sistema determina o estado REGULAR ligando os acionadores visuais amarelos e a mensagem de cuidado e desligando os demais acionadores, avisando visualmente e por mensagem que a estrutura está em uma situação comprometedora. Testes 4 e 5: Observa-se que nas medidas de 44cm e 49cm respectivamente, o sistema determina o estado LIMITE e aciona nestes casos os atuadores correspondentes para alertar tal situação: atuador visual amarelo ligado, mensagem de alerta atuador ligado e os demais atuadores desligados com o que alerta visualmente e por mensagem que a estrutura está comprometida e com risco de desabamento. Teste 6: Observa-se que a medida de 50cm o sistema determina o estado LIMITE e aciona os três atuadores correspondentes para alertar tal situação: atuador acústico ligado, atuador visual vermelho ligado, atuador de mensagem de alerta ligado e os demais atuadores desligados com o que alerta visualmente que a estrutura está seriamente comprometida e com risco de perda de prumo.
O estado limite inferior calculado em (4) é 42cm, então seria de se esperar que uma medida de deslocamento relativo maior que isso ativasse os alertas e uma medida menor não os ativasse. No Teste 2 com medida de 37cm os alertas são ativados de precaução com a qual se verifica que o sistema não espera o limite inferior para reagir. Da mesma forma, para o estado limite superior calculado em (5) é de 52,5cm, pelo que seria de esperar que a partir desta medição de deslocamento relativo do pavimento a estabilidade da estrutura ficasse seriamente comprometida, nos resultados do Ensaio 6 observa-se que com uma medida de 50cm, ou seja, uma medida inferior ao limite superior, o sistema localiza um estado de PERIGO e aciona os três atuadores correspondentes para alertar tal situação, isso valida que o sistema reage de forma dosada e não responder apenas a máximos e mínimos de acordo com o projeto feito.
5. DiscussÃo de resultados
O monitoramento de integridade estrutural utiliza principalmente sensores de deslocamento a laser e acelerômetros, o que representa um alto custo e alta complexidade técnica para seu gerenciamento, além de geralmente exigir pontos fixos para realizar a referida medição.
Li e Hao, (2016) relatam o desenvolvimento de um sensor de deslocamento relativo que usa o princípio de um circuito de ponte de Wheatstone e determina um índice de dano, com a limitação de que o sensor mede o movimento relativo local e é apenas sensível a mudanças de condição localmente.
Em Park et al. (2013) empregam um sensor de deslocamento a laser e um nó sensor sem fio personalizado que mede o deslocamento como um índice de dano com o qual implementam o SHM para verificar e corrigir os parâmetros de projeto de um edifício irregular. Este método envolve o uso da técnica óptica LDS para obter a distância do alvo por triangulação com sua complexidade inerente.
Nossa proposta baseada em um sistema de sensores ultrassônicos de deslocamento relativo pêndulo (SSDRUP) é capaz de fornecer a medição do deslocamento relativo da história por meio de uma única medição, e requer apenas que os sensores sejam colocados apontando para o elemento estrutural vertical do lado da força horizontal de entrada que é identificada e a coleta da medição será feita aproveitando o efeito pendular que é propiciado. Nos adequamos ao que foi determinado por Paulay, (2001) que indica que para avaliar devemos considerar que as magnitudes de deslocamento médio entre andares do último entre andares não devem ultrapassar 2 a 2,5% da altura do pavimento e com isso podemos estabelecer o limite da medida de deslocamento relativo e fornecer nosso próprio índice de dano para o SHM.
Nas três propostas, diferentes sensores de deslocamento relativo foram desenvolvidos e um índice de dano específico foi proposto para cada caso, portanto não é possível estabelecer uma comparação de eficiência.
6. ConclusÕes
A proposta de localização dos sensores e o efeito pêndulo causado pela sua colocação suspensa foi bem-sucedida, pois as projeções geométricas geradas uma vez analisadas possibilitaram através da coleta de uma única medição para cada sensor suspenso e aquela para efeito da força lateral que entra na estrutura esta medida diminui e através da relação de semelhanças que se pode aplicar, como é o caso, a triângulos semelhantes e foi possível obter através dos correspondentes mecanismos matemáticos a medida do deslocamento relativo do mezanino. O sistema requer apenas uma calibração simples com o eixo de referência vertical.
A aplicação do projeto hierárquico da lógica programável com programação VHDL permitiu o projeto de um dispositivo eletrônico capaz de obter medições coletadas pela rede de sensores para serem processadas pelo algoritmo SSDRUP para entregar medições de deslocamento relativo do pavimento, bem como identificar aquela de maior magnitude com a qual o algoritmo SBR para SSDRUP realiza a avaliação para determinar a estabilidade da estrutura através do índice proposto apresentado neste trabalho.
A instrumentação com SBR para SSDRUP do modelo utilizado nesta investigação forneceu as informações necessárias para a avaliação. Na seção de resultados, pode-se verificar como o sistema foi capaz de determinar em cada caso saídas para os atuadores e que 100% dos testes executados corresponderam exatamente ao projeto estabelecido e às ações definidas pelo especialista. Com o que podemos concluir que o sistema SBR para SSDRUP é capaz de determinar a estabilidade de uma estrutura modelo de forma não invasiva, em tempo real, sem a necessidade de exigir pontos fixos para coleta de dados e com base em um parâmetro: o deslocamento relativo ao pavimento pode ser recomendado como ferramenta de apoio para uso em SHM para estimar danos em edifícios de vários andares.
7. Agradecimentos
Os autores agradecem ao Centro de Investigación Multidisciplinar Aragón-FES Aragón, UNAM, México, pelo apoio no desenvolvimento deste projeto. F. Ramírez agradece a bolsa de doutorado do Conacyt.
REFERÊNCIAS
Arias, D., De la Colina, J. (2018), Assessment of methodologies to estimate displacements from measured acceleration records. Measurement. 114:261-273. https://doi.org/10.1016/j.measurement.2017.09.019
Bao, X., Chen, L. (2012), Recent progress in distributed fiber optic sensors. Sensors. 12(7):8601-8639. https://doi.org/10.3390/s120708601
Breuer, P., Chmielewski, T., Górski, P., Konopka, E. (2002), Application of GPS technology to measurements of displacements of high-rise structures due to weak winds. Journal of Wind Engineering and Industrial Aerodynamics. 90(3):223-230. https://doi.org/10.1016/S0167-6105(01)00221-5
Chatterjee, S., Sarbartha, S., Sirshendu, H., Nilanjan, D., Amira, S., Valentina, E. (2017), Particle swarm optimization trained neural network for structural failure prediction of multistoried RC buildings. Neural Computing and Applications. 28:2005-2016. https://doi.org/10.1007/s00521-016-2190-2
Ghasemi, M. R., Nobahari, M., Shabakhty, N. (2018), Enhanced optimization-based structural damage detection method using modal strain energy and modal frequencies. Engineering with Computers. 34:637-647. https://doi.org/10.1007/s00366-017-0563-5
Guo, J., Xie, X., Bie, R., Sun, L. (2014), Structural health monitoring by using a sparse coding-based deep learning algorithm with wireless sensor networks. Personal and Ubiquitous Computing. 18:1977-1987. https://doi.org/10.1007/s00779-014-0800-5
Li, J., Hao, H. (2016), Health monitoring of joint conditions in steel truss bridges with relative displacement sensors. Measurement. 88:360-371. https://doi.org/10.1016/j.measurement.2015.12.009
Li, X. Q., Chen, Q. J., Ding, Z. D. (2019), Structural damage diagnosis and fine scale finite element intelligence simulation of long span cable stayed bridges. Cluster Computing. 22: 4101-4107. https://doi.org/10.1007/s10586-017-1515-y
Maxinez, D., Alcalá, J. (2007), VHDL El arte de programar sistemas digitales. México, CECSA, 5th. ed., cap 1, pp. 1-31.
Moosazade, S., Namazi, E., Aghababael, H., Marto, A., Mohamad, H., Hajihassani, M. (2019), Prediction of building damage induced by tunnelling through an optimized artificial neural network. Engineering with Computers. 35(2):579-591. https://doi.org/10.1007/s00366-018-0615-5
Park, H. S., Kim, J. M., Choi, S. W., Kim, Y. (2013), A Wireless Laser Displacement Sensor Node for Structural Health Monitoring. Sensors. 13(10):13204-13216. https://doi.org/10.3390/s131013204
Paulay, T., (2001) Some design principles relevant to torsional phenomena in ductile buildings. Journal of Earthquake Engineering. 5(3):273-308. https://doi.org/10.1080/13632460109350395
Song, H. X., Wang, X. D., Ma, L. Q., Cai, M. Z., Cao, T. Z. (2006), Design and performance analysis of laser displacement sensor based on Position Sensitive Detector (PSD). Journal of Physics: Conference Series. 48:217-222. http://dx.doi.org/10.1088/1742-6596/48/1/040
Tamura, Y., Matsui, M., Pagnini, L. C., Ishibashi, R., Yoshida, A. (2002), Measurement of wind-induced response of buildings using RTK-GPS. Journal of Wind Engineering and Industrial Aerodynamics. 90:1783-1793. https://doi.org/10.1016/S0167-6105(02)00287-8
Zrelli, A., Ezzedine, T. (2017), Collect Tree Protocol for SHM system using wireless sensor networks. 13th International Wireless Communications and Mobile Computing Conference (IWCMC):1797-1801. https://doi.org/10.1109/IWCMC.2017.7986556
