| Artículos | https://doi.org/10.21041/ra.v12i3.592 |
Avaliação da influência da corrosão na estabilidade global de colunas em concreto armado
Evaluation of the influence of corrosion on the global stability of reinforced concrete columns
Evaluación de la influencia de la corrosión en la estabilidad global de las columnas de hormigón armado
Maiara
Feliciano dos Santos1
![]() ,
Danilo
Pereira dos Santos2
*
,
Danilo
Pereira dos Santos2
*
![]()
1 Fundação Hermínio Ometto (FHO | Uniararas), Araras, Brasil.
² Universidade Federal Tecnológica do Paraná (UTFPR), Curitiba, Brasil.
*Contact author: danilo.pereira@engenharia.ufjf.br
Recepção:
01
de
março
de
2022.
Aceitação:
08
de
julho
de
2022.
Publicação: 01 de setembro de 2022.
| Citar como:Santos, M. F., Santos, D. P. (2022), “Avaliação da influência da corrosão na estabilidade global de colunas em concreto armado”, Revista ALCONPAT, 12 (3), pp. 401 – 422, DOI: https://doi.org/10.21041/ra.v12i3.592 |
Resumo
Este trabalho analisa o impacto da corrosão na estabilidade global de colunas em concreto armado, avaliando a eficácia dos critérios de redução de rigidez propostos pela ABNT NBR 6118:2014. A partir das análises, utilizando-se modelos em elementos finitos que reproduziram o comportamento dos materiais, definiu-se que a corrosão causa a intensificação dos esforços globais de segunda ordem na estrutura. Entretanto, em situações críticas, a perda de equilíbrio na seção transversal conduziu à falha estrutural antes mesmo da perda de estabilidade. O estudo foi realizado tanto por meio de uma análise não-linear geométrica, quanto pela aplicação do coeficiente γz, onde concluiu-se que a posterior adição de efeitos reológicos pode conduzir a uma configuração que ultrapasse os limites propostos pela norma brasileira.
Palavras chave:
concreto,
corrosão,
estabilidade global,
efeitos de segunda ordem
1. IntroduÇÃo
A corrosão pode ser entendida como a interação destrutiva entre o material e o meio em que se encontra, desencadeada por ações eletroquímicas, químicas, físicas ou pela união destas, constantemente provocada pela ação de cloretos ou pelo desenvolvimento de fissuras. A presença da corrosão em regiões com tensões de tração é a situação mais gravosa, já que pode ocasionar a ruptura frágil da seção sem que ocorra deformação prévia da estrutura (Helene, 1993; Schvartzman et.al., 2010).
As armaduras de aço dispostas no concreto se encontram protegidas por uma película de óxido de ferro que se forma na superfície do metal devido à alcalinidade do concreto, garantindo sua passivação. Entretanto, esta película pode ter sua integridade comprometida com a redução do pH para abaixo de nove, resultado da carbonatação do concreto na camada de cobrimento, que ocorre devido à presença de íons cloreto, em taxas críticas de poluição atmosférica ou com a lixiviação do concreto, podendo ser intensificados por condições adversas do meio, tipo ou idade da construção (Maldonado-Bandala et. al., 2018; Araujo et. al., 2020; Silvestro et. al., 2020).
O emprego de espessuras inadequadas no cobrimento, devido a erros de projeto ou de execução, pode comprometer a proteção necessária para manter a integridade das barras de aço (Fusco, 2008; Malheiro et. al., 2014; Felix e Carrazedo, 2021). Além disso, a escolha do cimento, aditivos e adições pode mitigar ou intensificar o potencial corrosivo (Silva et. al., 2015; Trevisol et. al., 2017; Dietrich et. al., 2017; Teixeira et. al., 2021).
A corrosão do aço resulta em um hidróxido fraco, pulverulento, sem aderência ou coesão denominado ferrugem, que aumenta seu volume à medida que se forma e pode chegar a ter de oito a dez vezes o volume de aço do qual se originou. As partículas que enferrujam pressionam o concreto ao redor, desencadeando a degradação da estrutura. (Verçoza, 1991; Balestra et. al., 2018).
Diversos estudos procuram reproduzir as condições de deterioração em laboratório por meio de ensaios acelerados (Meira e Ferreira, 2019), outros procuram investigar o impacto que diferentes adições têm sobre o concreto no que diz respeito ao seu potencial corrosivo (Amorim Júnior et. al., 2021; Santos et. al., 2020; Blanco et. al., 2019; Figueiredo et. al., 2014). Tais esforços se tornam cada vez mais necessários, uma vez que a estimativa do início deste século apontou que até 3,5% do produto interno bruto de um país desenvolvido é reinvestido para contornar os efeitos da degradação por corrosão (Mackechnie e Alexander, 2001). Diante disso, são crescentes os investimentos em modelos matemáticos que possam descrever a degradação estrutural ocasionada pela corrosão.
Pesquisas recentes têm explorado a simulação numérica da difusão de cloretos em concreto, como os trabalhos de Ayinde et. al. (2017) e de Souza e Leonel (2021), ou por meio de análises de confiabilidade baseadas em modelos probabilísticos (Felix et. al., 2020; Ramos e Carrazedo, 2021; Favretto et. al., 2021). Outras aplicações utilizam o método dos elementos finitos, como a proposta por Ramos e Carrazedo (2020), que desenvolveram modelos capazes de descrever as diferentes fases do concreto armado e a propagação do dano causado pelo processo corrosivo.
Portanto, o presente trabalho busca contribuir com esta área do conhecimento, adicionando ao problema a avaliação da estabilidade global de uma estrutura degradada. Para isso, reproduziu-se numericamente o comportamento mecânico do concreto, bem como a evolução do dano quando este está submetido a cargas externas e à corrosão das armaduras. Tal modelo foi construído com a aplicação do Método dos Elementos Finitos (MEF), conforme discutido ao longo do trabalho.
2. Procedimento
O uso de simulações numéricas para a previsão do comportamento de estruturas em concreto armado, na presença do dano, exige a reprodução satisfatória do comportamento mecânico dos materiais constituintes frente solicitações externas. Para isso, foram definidos modelos constitutivos que caracterizam os materiais nas análises realizadas. Nesta seção serão descritos todos os parâmetros utilizados para simular o comportamento mecânico do concreto armado, tal como a validação dos modelos constitutivos utilizados.
2.1 Modelos constitutivos dos materiais
Materiais que reproduzem o comportamento do aço e do concreto foram adicionados aos elementos modelados, contendo características como a densidade, o módulo de elasticidade e o coeficiente de Poisson.
No caso do concreto, por conta do desenvolvimento natural de fissuras, se fez necessário a adição de mais informações para que o material reproduzisse fielmente o seu comportamento à tração, compressão, acúmulo de deformações inelásticas e dano.
Os modelos constitutivos empregados aos materiais, concreto e aço, foram extraídos do código europeu CEB-FIB (2010). Assim, o intuito principal desta etapa é a reprodução do comportamento mecânico do concreto armado, de sua curva tensão x deformação, incluindo a influência da aplicação de um modelo de dano.
2.1.1 Modelo constitutivo do aço
O modelo constitutivo empregado ao aço caracteriza o seu comportamento na presença de tensões de tração, representado no diagrama da Figura 1, ou compressão. O primeiro trecho representa a resposta linear do material até que o valor característico da resistência ao escoamento do aço em tração (f yk ) seja atingido, seguido de um segundo trecho linear que corresponde ao seu escoamento com encruamento até atingir o valor característico da resistência à tração do aço (f tk ), que ocorre no valor característico de deformação máxima (ε uk ).
As tensões no aço (σ s ) foram obtidas por meio da Equação (1), com os valores do módulo de elasticidade do aço (E s ) e da deformação do aço (ε s ).
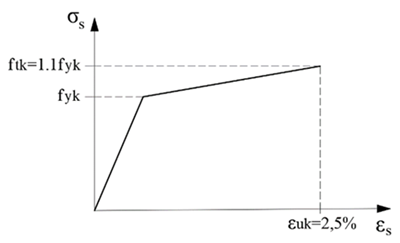
Figura 1.
Diagrama tensão x deformação do aço tracionado (Adaptado de CEB-FIB, 2010)
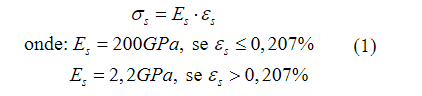
2.1.2 Modelo constitutivo do concreto
O modelo constitutivo utilizado no concreto caracteriza o seu comportamento frente solicitações de compressão (Figura 2), e tração (Figura 3 e Figura 4).
Quando comprimido, o concreto apresenta um comportamento elástico até atingir o seu valor médio de resistência à compressão (f cm ), passando a perder rigidez. A partir deste ponto, o desenvolvimento de microfissuras causa o amolecimento do material, representado no trecho decrescente do diagrama.
O concreto tracionado apresenta um comportamento elástico linear até atingir a deformação de tração do concreto (ε ct ) de 0,15‰. Em aproximadamente 90% do valor médio da resistência à tração axial do concreto (f ctm ), o desenvolvimento de microfissuras causa a diminuição da rigidez do material, caracterizando uma zona de fissuração. Em tensões próximas ao f ctm o quadro se intensifica, uma vez que ocorre a evolução das fissuras. A partir desse ponto, o material sofre uma redução drástica em sua rigidez.
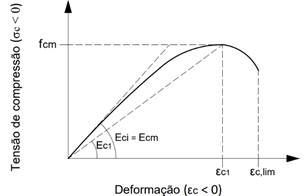
Figura 2.
Diagrama tensão x deformação do concreto comprimido (Adaptado de CEB-FIB, 2010)
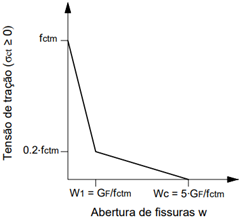
Figura 4.
Diagrama tensão x abertura de fissuras na zona de fratura (Adaptado de CEB-FIB, 2010)
O f cm foi definido por meio da Equação (2), a partir do valor característico da resistência à compressão do concreto (f ck ) e do valor padronizado que representa a diferença entre a resistência média do concreto e a sua resistência característica (∆ f ).
O módulo secante desde a origem até o pico da tensão compressiva (E C1 ) foi definido utilizando-se a Equação (3). Nesta equação tem-se as deformações de compressão do concreto (ε c ), variando de zero à deformação final em compressão (ε c,lim ) de 3,5‰, e a deformação de compressão máxima (ε c1 ), esta última obtida por meio dos valores tabelados que constam no CEB-FIB (2010).
A Equação (4) foi utilizada para determinar o módulo de elasticidade do concreto aos 28 dias (E ci ), que depende do módulo de elasticidade tangente inicial (E c0 ), do parâmetro em função da natureza do agregado (α E ) e do valor padronizado (∆ f ), definidos por consulta ao CEB-FIB (2010).
O valor da razão entre as deformações (η) e da constante de plasticidade (k) foram definidos por meio da Equação (5) e Equação (6), respectivamente. Por fim, utilizou-se a Equação (7) para calcular os valores de tensão de compressão do concreto (σ c ) e obter a lei tensão x deformação apresentada no diagrama da Figura 2.
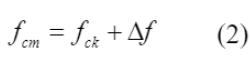 |
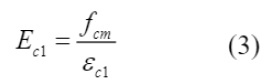
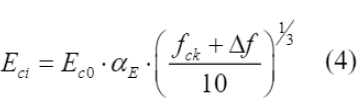
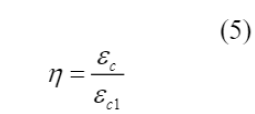
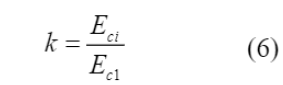 |
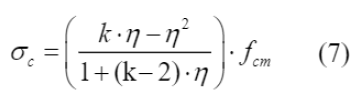
A resistência à tração axial do concreto (f ctm ) foi definida através da Equação (8) e Equação (9), de acordo com o seu f ck .
Na zona de fratura as tensões e deformações estão relacionadas a uma abertura de fissuras fictícia (w), sendo seus valores em pontos específicos, (w 1 ) e (w c ), obtidos por meio da Equação (10) e Equação (11), respectivamente. Finalmente, a energia de fratura (G F ) foi obtida por meio da Equação (12).
Vale salientar que apenas o conhecimento da abertura de fissuras em função da energia de fratura não se mostra suficiente para muitas aplicações. Sendo assim, Aitsin et. al. (2008) trazem a definição do comprimento característico (l ch ), um valor útil para a avaliação da abertura de fissuras quanto à deformação. Esta grandeza é obtida a partir da Equação (13).
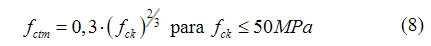

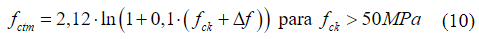
As deformações específicas (ε
t
) tiveram seus valores variando de zero ao valor final da abertura de fissuras fictícia (w
c
), convertido a partir da razão entre w
c
e l
ch
. Os valores de tensão de tração (σ
t
) foram definidos até uma deformação de 0,15‰ por meio da Equação (14) e Equação (15), de acordo com o f
ctm
. Na zona de fratura, os valores de σ
t
foram determinados utilizando-se a Equação (16) e Equação (17), em um intervalo variando de 0,15‰ a w
c
.
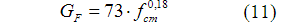
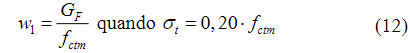
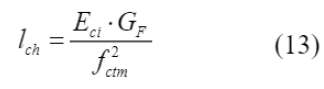

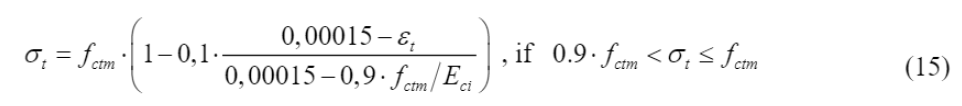
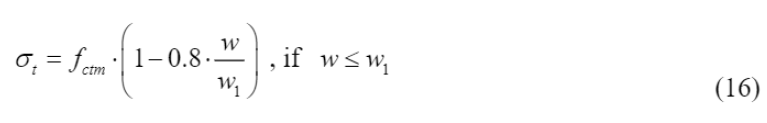
Ao concluir os cálculos, os valores de σ
c
e σ
t
foram adicionados ao modelo de dano aplicado ao material que representa o concreto nas simulações numéricas realizadas.
2.1.2.1 Modelo de dano aplicado ao concreto
O modelo adotado para o concreto foi o Concrete Damage Plasticity (CDP), um modelo de dano com plastificação desenvolvido por Lubliner et. al. (1989) e aperfeiçoado por Lee e Fenves (1998).
Tal modelo está implementado e disponível no software Abaqus®.
Para este modelo de material, o comportamento na presença do dano se encontra representado nos diagramas da Figura 5 e Figura 6 e é matematicamente descrito pelas leis tensão x deformação indicadas na Equação (18), para a compressão, e Equação (19), para a tração, propostas por Hibbitt et. al. (2011).
Tanto na tração quanto na compressão, enquanto íntegro, o concreto apresenta uma conservação em seu módulo de elasticidade inicial (E
0
). Ao se atingir a tensão máxima na tração (σ
tu
) ou na compressão (σ
cu
), inicia-se o processo de degeneração deste módulo de elasticidade à medida que são incrementadas as variáveis de dano d
t
(tração) e d
c
(compressão). As deformações plásticas à tração ε
t
pl
e à compressão ε
c
pl
incorporam a plastificação ao modelo.
As variáveis de dano d
c
e d
t
foram obtidas por meio da Equação (20) e Equação (21), respectivamente, propostas por Yu et. al. (2010), com os valores de σ
c
, σ
t
, f
cm
e f
ctm
já definidos anteriormente.
Por fim, os valores das variáveis de dano d
c
e d
t
, obtidos com os cálculos, foram adicionados ao modelo de dano do concreto.
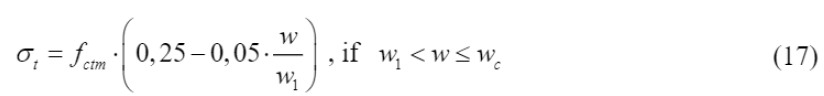
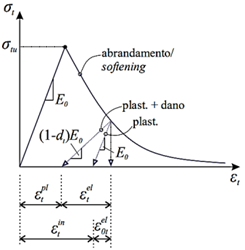
Figura 5.
Relação tensão x deformação para o concreto na tração (Extraído de Reginato, 2020)
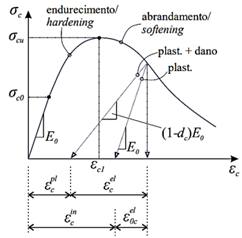
Figura 6.
Relação tensão x deformação para o concreto na compressão (Extraído de Reginato, 2020)
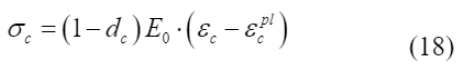
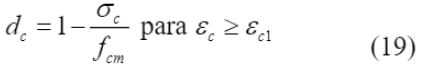
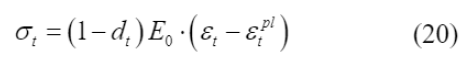
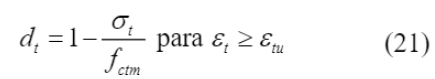 |
2.2 Validação dos modelos constitutivos
A fim de analisar se os modelos constitutivos utilizados na caracterização dos materiais garantem o comportamento esperado, foram realizadas simulações numéricas no software Abaqus®. Nesta primeira etapa foram realizadas três análises, uma para verificar o comportamento do aço tracionado, em um elemento de barra bidimensional, e as outras duas para verificar o comportamento do concreto tracionado e comprimido, em um elemento sólido bidimensional.
As propriedades elásticas adicionadas aos materiais, como o módulo de Young (E) e o coeficiente de Poisson (ν), foram extraídas de Álvares (1993). Além disso, antes que as análises fossem realizadas, as malhas de elementos finitos aplicadas nos modelos passaram por testes de convergência.
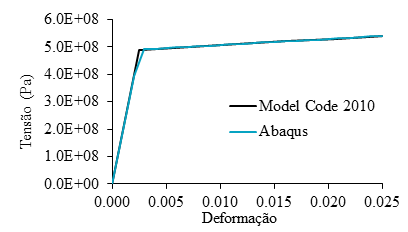
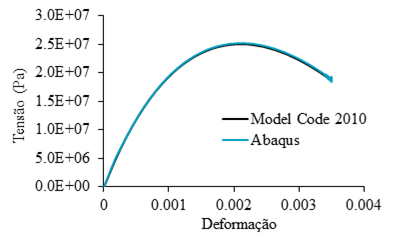
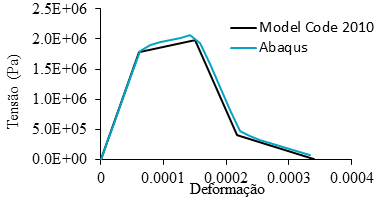
Os resultados obtidos com as simulações numéricas foram comparados aos modelos teórico-analíticos propostos no CEB-FIB (2010), estando representados na Figura 7, Figura 8 e Figura 9.
Com as análises, foi possível definir que o modelo constitutivo utilizado na modelagem numérica do aço garantiu o comportamento esperado, apresentando apenas um desvio sútil no início do trecho que representa seu escoamento com encruamento. Quanto ao concreto, as análises permitiram observar que o material numericamente representado simulou satisfatoriamente o comportamento previsto, apresentando apenas variações modestas nas zonas de falha e de fratura.
 |
||||
| Figura 7. Diagrama comparativo tensão x deformação do aço tracionado | ||||
 |
||||
| Figura 8. Diagrama comparativo tensão x deformação do concreto comprimido | ||||
 |
||||
| Figura 9. Diagrama comparativo tensão x deformação do concreto tracionado | ||||
Os modelos constitutivos validados foram aplicados na simulação numérica não linear de uma viga em concreto armado sujeita à aplicação de cargas. Para isso, foi realizada a modelagem tridimensional, empregando elementos sólidos paralelepipédicos lineares de 8 nós, simulando o concreto, e elementos de barra tridimensionais em aço, representando os vergalhões e estribos, no software Abaqus®. Considerou-se perfeita aderência entre o aço e o concreto, obtida por meio do embutimento das barras de aço no elemento de concreto.
As dimensões, a taxa de armadura, o local da aplicação das cargas na viga e as propriedades elásticas dos materiais, Tabela 1, foram registradas por Álvares (1993). A malha estruturada de elementos finitos aplicada no modelo passou por testes de convergência, por meio da realização de análises lineares iterativas, aumentando-se o número de elementos, até que o deslocamento no centro da viga deixasse de sofrer alterações.
| Tabela 1. Propriedades elásticas dos materiais (Adaptado de Álvares, 1993) | ||||||||||||||
| Material | Coeficiente de Poisson | Módulo de Young (MPa) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Concreto | 0.2 | 29200 | ||||||||||||
| Aço | 0.3 | 196000 | ||||||||||||
A análise foi realizada até um deslocamento de 8 mm no centro da viga, correspondendo a uma carga P de aproximadamente 47 kN. Conforme a aplicação progressiva das cargas era efetuada, sob a forma de deslocamentos prescritos, os deslocamentos no centro da viga foram registrados.
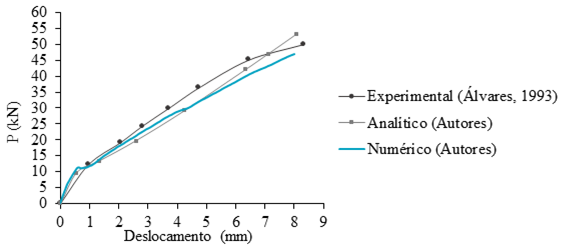
Por fim, os resultados foram comparados aos obtidos na análise experimental de Álvares (1993) e ao modelo teórico deduzido pelos autores, a partir das hipóteses de fissuração proposta por Branson (1968). O modelo de Branson (1968) permite a consideração de uma inércia média, que leva em conta os efeitos da fissuração ao longo do vão do elemento estrutural, a partir de uma análise semiprobabilística. Tais comparações se encontram representadas na Figura 10.
 |
||||
| Figura 10. Diagrama comparativo carga x deslocamento das análises | ||||
A viga da simulação numérica se comportou de maneira semelhante à análise experimental e ao modelo analítico nos Estádios I e II. Divergências sutis foram observadas, mas se justificam pelas incertezas associadas aos parâmetros de caracterização do concreto. Além disso, há divergências sensíveis entre as condições de contorno adotadas no modelo numérico e aquelas presentes no ensaio experimental.
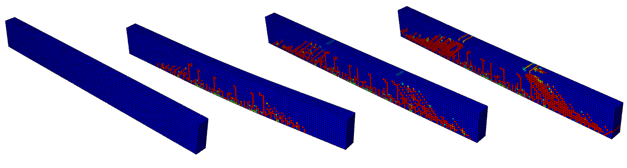
Com a simulação numérica, foi possível observar também a evolução do dano na estrutura, representada na Figura 11. Houve o desenvolvimento e propagação de fissuras no elemento conforme a aplicação das cargas, até atingir-se um estado elevado de degradação, de maneira muito semelhante à observada por Álvares (1993) em sua análise experimental.
 |
||||
| Figura 11. Evolução de fissuras na viga | ||||
Após a confirmação da eficiência dos modelos constitutivos aplicados, tal como do modelo de dano utilizado para representar a degradação do concreto, foi realizada a modelagem de uma estrutura no Software Abaqus®, onde a corrosão foi adicionada às análises conforme será discutido nas seções seguintes.
2.3 Modelagem da estrutura sujeita à corrosão
Nesta etapa, serão apresentadas a idealização da estrutura estudada, a estratégia para a simulação numérica da degradação provocada pelo fenômeno da corrosão nas armaduras e a metodologia para a avaliação da estabilidade global. Também serão dadas informações sobre a construção do modelo em elementos finitos de modo a permitir a reprodutibilidade da pesquisa.
2.3.1 Características geométricas da estrutura
A estrutura escolhida para as simulações se baseia na apresentada por Wahrhaftig (2008), Figura 12. Trata-se de uma estrutura de seção vazada e esbelta em concreto armado, utilizada como suporte para um sistema de transmissão telefônica. Embora as dimensões reproduzidas no modelo numérico não sejam as mesmas da estrutura real, guardou-se a proporção quanto ao índice de esbeltez da estrutura. Assim, o elemento estrutural foi modelado com 14 m de altura e se encontra armado com 16 barras de aço de 25 mm, dispostas conforme a Figura 12.
Tanto a estrutura de concreto quanto as barras de aço foram modeladas com elementos sólidos lineares paralelepipédicos de 8 nós. As condições de contorno aplicadas no modelo são compostas por um carregamento vertical pontual de 5 kN, posicionado no topo do elemento, como representação das antenas, e por um engaste, posicionado na base do elemento, ambos adicionados no ponto central da seção. Ademais, as forças horizontais que caracterizam a ação do vento foram adicionadas ao modelo sob a forma de cargas pontuais a cada 1 m da estrutura. Finalmente, o peso próprio foi considerado para uma gravidade de 9,81 m/s, tendo as massas específicas do concreto e do aço, extraídas da ABNT NBR 6120:2019, iguais a 2400 kg/m³ e 7850 kg/m³, respectivamente.
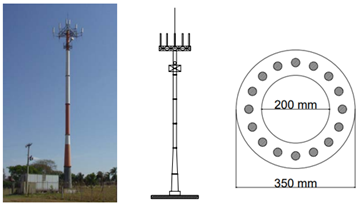
Figura 12.
Estrutura real aproximada pelo modelo numérico (Adaptado de Wahrhaftig, 2008)
2.3.2 Estimativa do vento
O vento foi estimado através de equações extraídas da ABNT NBR 6123:1988 e aplicado à estrutura como forças pontuais horizontais, a cada metro, na lateral esquerda do elemento estrutural.
Inicialmente, calculou-se o valor do fator S 2 , que considera a influência da rugosidade do terreno, das dimensões da edificação e de sua altura sobre o terreno, por meio da Equação (22). Com o valor do fator topográfico S 1 , considerando o terreno plano ou fracamente acidentado, do fator S 2 calculado, do fator estatístico S 3 , considerando uma edificação cuja ruína total ou parcial pode afetar a segurança ou possibilidade de socorro a pessoas após uma tempestade destrutiva, e da velocidade básica do vento (V 0 ), definida com base na localização da estrutura. A velocidade básica do vento é uma grandeza necessária para a determinação da velocidade característica do vento, V k (Equação (23)).
Assim, após estas definições, foi calculada a pressão dinâmica (q), através da Equação (24), tal valor é útil ao cálculo das forças pontuais adicionadas ao modelo.
Portanto, calculou-se a força de arrasto (F a ), Equação (25), com os valores do coeficiente de arrasto (C a ), do fator de redução (K), da distância vertical entre as forças (H) e do diâmetro externo da seção (D). Tais valores de F a , calculados a cada metro, correspondem à intensidade das forças horizontais aplicadas na estrutura.

2.3.3 Adição da corrosão
A corrosão foi adicionada ao modelo com o intuito de verificar qual a sua influência na estabilidade da estrutura. A expansão gerada pelos produtos da corrosão foi representada por meio da aplicação de deslocamentos radiais prescritos em extensões pré-estabelecidas do concreto em contato com as barras de aço acometidas pela corrosão, sendo posicionados na região mais afetada pela ação do vento na estrutura. O método utilizado para a definição dos valores dos deslocamentos radiais aplicados foi proposto por El-Maaddawy e Soudki (2007).
A constante de flexibilidade do furo (k) foi obtida por meio da Equação (26). Trata-se de uma constante que relaciona o deslocamento radial com a pressão de corrosão, levando em consideração a zona porosa presente na interface de contato entre o aço e o concreto, que deve ser incialmente preenchida pelos produtos da corrosão antes que as tensões expansivas geradas comecem a criar pressão sobre o concreto ao redor. Para isso, usou-se os valores do coeficiente de Poisson (ν), do módulo de elasticidade efetivo (E
ef
), do diâmetro das barras de aço (D), da espessura da zona porosa (δ
0
), variando de 10 a 20 μm, e do fator (Ψ) calculado com a Equação (27), que leva em conta o cobrimento de concreto (C).
A pressão radial necessária para produzir deslocamentos no concreto (P
cor
) foi calculada por meio da Equação (28), onde o valor da porcentagem de perda de massa de aço (m
1
) variou de acordo com a classe de resistência do concreto. Por fim, foi possível definir os valores de deslocamento no concreto (δ
c
), necessário para acomodar o aumento de volume decorrente da transformação do aço em ferrugem, por meio da Equação (29).
A porcentagem de perda de massa de aço (m
1
) pode ser relacionada com a massa de aço consumida por unidade de comprimento (M
loss
) por meio da Equação (30), com os valores do diâmetro das barras de aço (D) e da densidade do aço (ρ
s
).
2.4 Metodologia para estudo da estabilidade global
Inicialmente, foram realizadas três simulações no software Abaqus®, com o intuito de verificar a estabilidade da estrutura com diferentes classes de resistência do concreto, variando do C20 ao C50. Foram verificados o valor do deslocamento no topo e do momento na base da estrutura em cada análise realizada.
A primeira etapa consistiu no cálculo do coeficiente γ
z
conforme a ABNT NBR 6118:2014, Equação (31), com os valores de deslocamento a cada metro da estrutura, medidos na primeira análise (AN1), ou seja, uma análise elástica e linear com redução do módulo de elasticidade (E) em 20% (em acordo com o item 15.7.3 da ABNT NBR 6118:2014).
O coeficiente γ
z
permite avaliar a importância dos esforços de segunda ordem globais na estrutura e sua classificação quanto à deslocabilidade dos nós, sendo considerada uma estrutura de nós fixos aquela cujo valor do γ
z
for menor ou igual a 1,1. Tal coeficiente depende do momento de tombamento e da soma dos produtos de todas as forças verticais pelos deslocamentos horizontais de seus respectivos pontos de aplicação, obtidos na análise de 1ª ordem.
Na sequência, a Não Linearidade Geométrica (NLG) foi adicionada ao modelo AN1, dando origem à segunda análise (AN2), onde foi mantida a redução do módulo de elasticidade em 20%.
Com os valores de momento na base, obtidos na primeira e na segunda análise (AN1 e AN2), foi calculado um novo coeficiente γ
z
. Desta vez, o ∆M
tot,d
utilizado foi a diferença entre o momento obtido na segunda e na primeira análise, enquanto o valor de M
1,tot,d
foi o do momento da primeira análise (AN1). Este cálculo apenas ratificou a competência do coeficiente γ
z
como estimador dos efeitos de segunda ordem.
Finalmente, na terceira análise (AN3), o valor do E foi mantido íntegro e adicionou-se a Não Linearidade Física (NLF) e a NLG ao modelo. O coeficiente γ
z
, agora renomeado como γ
zcalc
, Equação (32), foi calculado e será apresentado nos resultados desta pesquisa.
Nesta etapa, a NLF foi adicionada às simulações por meio dos modelos constitutivos dos materiais e do modelo de dano, em substituição à redução do módulo de elasticidade em 20% dos modelos AN1 e AN2.
Onde
ΔMtot,d é a soma dos produtos das forças verticais atuantes pelos deslocamentos horizontais de seus respectivos pontos de aplicação, obtidos na análise de 1ª ordem M1,tot,d é o momento de tombamento (calculado a partir de uma análise elástica e linear)
Onde
M2,tot,d é o momento total calculado a partir de uma análise de 2ª ordem
M1,tot,d é o momento de tombamento (calculado a partir de uma análise elástica e linear)
Posteriormente, a corrosão foi adicionada ao modelo da terceira análise e foram realizadas mais oito simulações com cada classe de concreto. As primeiras quatro análises foram realizadas em um modelo acometido pela corrosão em três de suas dezesseis barras de aço, em uma extensão de 5 cm (AN4 a AN7). As demais foram realizadas em um modelo com a ação da corrosão em cinco de suas dezesseis barras de aço, em uma extensão de 10 cm (AN8 a AN11).
Em ambos os casos, a corrosão foi adicionada a uma distância de 30 cm da base do elemento, sendo esta próxima a região de momento máximo provocado pela ação do vento. Nesta etapa, o coeficiente γ
zcalc
foi calculado conforme descrito na Equação (32).
O resumo das análises realizadas se encontra no Quadro 1. Ademais, é importante destacar que em todas as análises foi considerada perfeita a aderência entre o aço e o concreto, com exceção das regiões degradadas pela corrosão.
Salienta-se que informações adicionais a respeito do coeficiente γ
z
, incluindo a sua dedução matemática, podem ser consultadas no trabalho de Franco e Vasconcelos (1991).
2.4.1 Malha de elementos finitos
A malha de elementos finitos adicionada ao modelo foi composta por elementos tridimensionais paralelepipédicos lineares, portanto, formados por 6 faces e 8 nós.
A convergência da malha aplicada ao modelo foi realizada por meio de simulações iterativas, sem a consideração de não-linearidades, aumentando-se o número de elementos finitos que compõem a malha, até que o valor do deslocamento no topo da estrutura deixasse de sofrer alterações.
3. Resultados e discussão
A corrosão foi adicionada ao modelo gradativamente, de tal maneira que o deslocamento aplicado foi maior em cada simulação realizada com cada classe de resistência do concreto, à medida que se aumentou a porcentagem de corrosão (m
1
). A equivalência entre os valores de m
1
, do deslocamento radial aplicado no concreto (δ
c
) e da massa de aço consumida por unidade de comprimento (M
loss
) utilizados nas simulações se encontram representados no Tabela 2.
Com as simulações, foi possível verificar que os dois parâmetros analisados, deslocamento no topo e momento na base da estrutura, aumentaram conforme o incremento de m
1
, demonstrando que a evolução da corrosão nas armaduras gera uma redução na rigidez da estrutura, causando a intensificação de suas reações por ocasião do incremento dos esforços de segunda ordem. Os valores dos momentos na base da estrutura, obtidos com as simulações, se encontram representados na Figura 13.
A Tabela 3 traz os valores calculados de γ
zcalc
para as simulações AN1, AN3 e para as simulações AN7, realizadas após a adição da corrosão, considerando todas as classes de concreto analisadas. Os valores apresentados para as simulações com a adição da corrosão foram os obtidos aplicando-a em 3 barras de aço do modelo, por atingir valores superiores de γ
zcalc
quando comparados à aplicação em 5 barras.
Os valores calculados dos coeficientes γ
zcalc
se encontram relacionados com os valores de m
1
na Figura 14. É possível observar que em todas as classes de resistência do concreto, em ambas as situações de corrosão propostas, o γ
zcalc
aumenta conforme o aumento de m
1
e, consequentemente, do deslocamento radial provocado pela corrosão, δ
c
.
Ao analisar os resultados apresentados na Tabela 3 e na Figura 14, constata-se que a adição da corrosão à simulação gerou um aumento no valor do coeficiente γ
zcalc
em todas as classes de resistência do concreto analisadas. Tendo em vista que o γ
zcalc
pode ser adaptado para um coeficiente de majoração dos esforços globais de 1ª ordem, provenientes dos carregamentos horizontais, é possível definir que a adição da corrosão causou a intensificação dos esforços globais de 2ª ordem na estrutura.
Ao relacionar os valores de γ
zcalc
obtidos na AN7 e AN1, foi possível definir que os efeitos de segunda ordem na estrutura com a adição da corrosão correspondem a aproximadamente 99,6% dos determinados pela NBR 6118:2014, em todas as classes de resistência do concreto. Assim, os valores obtidos com base na norma se mostraram superiores, demonstrando que a redução de rigidez proposta pela norma brasileira é capaz de acomodar o nível de corrosão avaliado neste trabalho.
Além disso, observou-se que os concretos com menor resistência sofrem mais com a ação da corrosão, já que apresentaram valores superiores de γ
zcalc
. Os concretos com um f
ck
maior, mesmo submetidos a valores superiores de m
1
, apresentaram resultados inferiores de γ
zcalc
, demonstrando maior resistência frente ações externas e à degradação.
A Figura 15, retirada do software Abaqus® após a realização das simulações numéricas, traz um conjunto de imagens de um corte da seção transversal da estrutura analisada, na região onde a corrosão foi adicionada, em 3 e em 5 barras de aço, com o concreto C40. É possível observar a evolução das fissuras no concreto em torno das barras de aço conforme o aumento do produto da corrosão. A Figura 15 traz o dano gerado por tensões de tração, medido através da variável DAMAGET (grandeza adimensional).
Com a evolução do dano, a convergência numérica é prejudicada, delimitando os valores de corrosão possíveis de serem analisados e indicando que a partir de certo nível a falha pode ocorrer não por instabilidades na estrutura, mas por um alto índice de degradação do concreto na seção transversal.
Assim como observado por Pereira Junior et. al. (2016), o dano se manifestou de forma intensa nas regiões tracionadas da estrutura e, conforme o aumento da fissuração, o encontro das microfissuras levou ao processo de fratura do material.
O concreto ao redor das barras de aço acometidas pela corrosão sofreu com o desenvolvimento de fissuras, tendo um aumento gradual de degradação conforme o aumento da porcentagem de corrosão. Finalmente, a conexão de fissuras desenvolvidas ao redor das barras aumentou os efeitos de segunda ordem na estrutura.
4. Conclusões
A corrosão, além da degradação do aço, desencadeia um processo de deterioração do concreto, comprometendo o desempenho da estrutura frente ações externas e reduzindo o seu tempo de vida útil, já que interfere em sua integridade, deixando-a ainda mais suscetível ao desenvolvimento de novas manifestações patológicas.
Este trabalho reproduziu uma metodologia para a simulação e validação do comportamento mecânico de elementos estruturais em concreto armado adicionando a este o efeito mecânico imposto pela corrosão, ou seja, a intensificação do processo de fissuração fruto do produto expansivo gerado.
Com o presente estudo, foi possível definir que a corrosão influencia negativamente na estabilidade de elementos em concreto armado, já que intensifica os esforços globais de 2ª ordem na estrutura. Ao comparar os valores do coeficiente γ
z
obtidos com as simulações após a adição da corrosão com os calculados a partir da NBR 6118:2014, foi possível definir que os métodos presentes na norma para a consideração das não linearidades físicas em projeto, através de modelos simplificados, são seguros para os níveis de corrosão analisados.
Entretanto, os modelos também indicaram que a partir de certo nível de corrosão, a falha estrutural associada à degradação do concreto, devido ao desenvolvimento de fissuras, pode ocasionar a perda do equilíbrio interno na seção transversal, isto é, antes mesmo que o aumento dos esforços de 2ª ordem seja crítico.
Além disso, a redução de rigidez proposta pela norma brasileira também deve considerar o efeito reológico do concreto armado, de modo que a presença conjunta destes efeitos e da corrosão podem conduzir a estrutura a um estado não previsto pelos modelos simplificados de cálculo. Desta forma, recomenda-se que pesquisas futuras analisem os efeitos reológicos na presença de intensos níveis de degradação, a fim de precisar o nível de segurança proporcionado pelas simplificações normativas neste cenário.
REFERÊNCIAS
Aitsin, A. C. et al. (2008), Constitutive modelling of high strength/high performance concrete. Internation Federation for Structural Concrete (FIB). Lausanne, Switzerland, p. 125.
Álvares, M. S. (1993), “Estudo de um modelo de dano para o concreto: formulação, identificação paramétrica e aplicação com o emprego do método dos elementos finitos”, Dissertação (Título de Mestre em Engenharia de Estruturas), Escola de Engenharia de São Carlos, Universidade de São Paulo, São Carlos, p. 123.
Amorim Júnior, N. S. A. et al. (2021), Durability and service life analysis of metakaolin-based geopolymer concretes with respect to chloride penetration using chloride migration test and corrosion potential. Construction and Building Materials, 287, 122970. https://doi.org/10.1016/j.conbuildmat.2021.122970
Araujo, A. D. et al. (2020), Current condition of the exposed concrete façades reinforcement of the Vilanova Artigas building: modern architectural heritage. Revista IBRACON de Estruturas e Materiais, 14. https://doi.org/10.1590/S1983-41952021000100013
Associação Brasileira de Normas Técnicas. (1988). NBR 6123: Forças devidas ao vento em edificações. Rio de Janeiro.
Associação Brasileira de Normas Técnicas. (2014). NBR 6118: Projeto de estruturas de concreto - Procedimentos. Rio de Janeiro.
Associação Brasileira de Normas Técnicas. (2019). NBR 6120: Ações para o cálculo de estruturas de edificações. Rio de Janeiro
Ayinde, O. O. et al. (2017), Numerical simulation of concrete degradation due to chloride-induced reinforcement corrosion. Proceedings of the 3rd international forum on energy, environment science and materials, v. 120.
Balestra, C. E. T. et al. (2018), Effect of corrosion degree on mechanical properties of reinforcements buried for 60 years. Revista IBRACON de Estruturas e Materiais, 11, 474-498. https://doi.org/10.1590/S1983-41952018000300003
Blanco, Y. D. et al. (2019), Natural additive (nopal mucilage) on the electrochemical properties of concrete reinforcing steel. Revista ALCONPAT, 9(3), 260-276. https://doi.org/10.21041/ra.v9i3.429
Branson, D. E. (1968), Procedures for computing deflections. ACI Journal, New York, n. 65.
Dietrich, Y. P. et al. (2017), Desempenho mecânico e análise da corrosão das armaduras em concretos produzidos com adição de resíduos de rochas ornamentais. Matéria (Rio de Janeiro), 22. https://doi.org/10.1590/S1517-707620170004.0225
El-Maaddawy, T., Soudki, K. (2007), A model for prediction of time from corrosion initiation to corrosion cracking. Cement & Concrete Composites, v. 29, p. 168-175. https://doi.org/10.1016/j.cemconcomp.2006.11.004
Favretto, F. et al. (2021), Modelos de estimativa do grau de saturação do concreto a partir das variáveis ambientais aplicados à análise de confiabilidade de estruturas de concreto armado atacadas por íons cloreto. Revista Matéria. 2021, 26(3): e13001. https://doi.org/10.1590/S1517-707620210003.13001
Fédération Internationale du Béton/International Federation for Structural Concrete. (2010). CEB-FIB MODEL CODE.
Felix, E. F. et al. (2020), Development and analysis of a numerical model of the reinforced concrete expansion due to uniform corrosion. Revista de la Asociación Latinoamericana de Control de Calidad, Patología y Recuperación de la Construcción, 10(3), 300-316. https://doi.org/10.21041/ra.v10i3.395
Felix, E. F., Carrazedo, R. (2021), Análise probabilística da vida útil de lajes de concreto armado sujeitas à corrosão por carbonatação via simulação de Monte Carlo. Matéria (Rio de Janeiro), v. 26. https://doi.org/10.1590/S1517-707620210003.13043
Figueiredo, C. P. et al. (2014), O papel do metacaulim na proteção dos concretos contra a ação deletéria de cloretos. Revista IBRACON de Estruturas e Materiais, 7, 685-708. https://doi.org/10.1590/S1983-41952014000400008
Franco, M., Vasconcelos, A. C. (1991). Practical assessment of second order effects in tall buildings. Colloquium on the CEB-FIB MC 90, COPPE/UFRJ, Rio de Janeiro, RJ.
Fusco, P. B. (2008), “Tecnologia do concreto estrutural: tópicos aplicados”. São Paulo: PINI.
Helene, P. R. L. (1993), “Contribuição ao estudo da corrosão em armaduras de concreto armado”, Tese (Livre-docência junto ao Departamento de Engenharia de Construção civil). Escola Politécnica, Universidade de São Paulo, São Paulo, p. 231.
Hibbitt, H. et al. (2011), Abaqus analysis user’s manual version, 6.10. Dassault Systèmes Simulia Corp.: providence, RI, USA.
Lee, J., Fenves, G. L. (1998), A plastic-damage model for cyclic loading of concrete structures. Journal of Engineering Mechanics, ASCE, v. 124, p. 892- 900. https://doi.org/10.1061/(ASCE)0733-9399(1998)124:8(892)
Lubliner, J. et al. (1989), A plastic-damage model for concrete. International Journal of solids and Structures, v. 25, n. 3, p. 299-326. https://doi.org/10.1016/0020-7683(89)90050-4
Mackechnie, J. R., Alexander, M. G. (2001), Repair principles for corrosion-damaged reinforced concrete structures. Research monograph, 5, 1-36.
Maldonado-Bandala, E. E. et al. (2018), Evaluation of pathological problems associated with carbonation and sulfates in a concrete tower with more than 50 years in service. Revista ALCONPAT, 8(1), 94-107. https://doi.org/10.21041/ra.v8i1.284
Malheiro, R. M. D. C. et al. (2014), Influência da camada do revestimento de argamassa na penetração de cloretos em estruturas de concreto. Ambiente Construído, 14, 41-55. https://doi.org/10.1590/S1678-86212014000100005
Meira, G. R., Ferreira, P. R. R. (2019), Revisão sobre ensaios acelerados para indução da corrosão desencadeada por cloretos em concreto armado. Ambiente Construído, 19, 223-248. https://doi.org/10.1590/s1678-86212019000400353
Pereira Junior, W. M. et al. (2016), Análise numérica de vigas de concreto com fibras de aço utilizando mecânica do dano. Revista IBRACON de estruturas e materiais, v. 9, n. 2, p. 153-191. https://doi.org/10.1590/S1983-41952016000200002
Ramos, É. S., Carrazedo, R. (2020), Cross-section modeling of the non-uniform corrosion due to chloride ingress using the positional finite element method. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 42(10), 1-18. https://doi.org/10.1007/s40430-020-02627-5
Ramos, É. S., Carrazedo, R. (2021), Numerical analysis of reinforced concrete beam subject to pitting corrosion. Ambiente Construído, 22, 201-222. https://doi.org/10.1590/s1678-86212022000100588
Reginato, L. (2020), “Contribuição ao projeto de consolos de concreto com base em simulações numéricas”. Dissertação (Título de Mestre em Engenharia de Estruturas), Escola de Engenharia de São Carlos, Universidade de São Paulo, São Carlos, p. 184.
Santos, B. et al. (2020), Effect of the addition of metakaolin on the carbonation of Portland cement concretes. Revista IBRACON de Estruturas e Materiais, 13, 1-18. https://doi.org/10.1590/S1983-41952020000100002
Schvartzman, M. M. A. M. et al. (2010), Avaliação da corrosão sob tensão em aço inoxidável AISI 321 em ambiente de reator nuclear. Matéria (Rio de Janeiro), 15, 40-49. https://doi.org/10.1590/S1517-70762010000100006
Silva, S. H. et al. (2015), Analytic Hierarchy Process to choose the cement type to protect reinforced concrete to corrosion caused by chloride ions attack. Revista ALCONPAT, 5(3), 174-189. https://www.scielo.org.mx/scielo.php?pid=S2007-68352015000300174&script=sci_arttext&%20tlng=en
Silvestro, L. et al. (2020), Penetração de cloretos em concretos expostos em zona de atmosfera marinha por um período de 9 anos. Ambiente Construído, 21, 101-118. https://doi.org/10.1590/s1678-86212021000100496
Souza, V. D. B., Leonel, E. D. (2021), Probabilistic chloride diffusion modelling in cracked concrete structures by transient BEM formulation. Revista IBRACON de Estruturas e Materiais, 15. https://doi.org/10.1590/S1983-41952022000400002
Teixeira, F. R. et al. (2021), Avaliação de propriedades relacionadas à penetração de cloretos em concretos produzidos com substituição parcial de cimento por resíduo de beneficiamento de rochas ornamentais. Matéria (Rio de Janeiro), 26. https://doi.org/10.1590/S1517-707620210003.13029
Trevisol, C. A. et al. (2017), Avaliação de inibidores de corrosão para estruturas de concreto armado. Matéria (Rio de Janeiro), 22. https://doi.org/10.1590/S1517-707620170004.0238
Verçoza, E. J. (1991), “Patologia das edificações”. [S.I.]: Sagra.
Wahrhaftig, A. M. (2008), “Uma avaliação experimental e numérica do efeito da rigidez geométrica na resposta dinâmica de estruturas esbeltas sujeitas à excitação de vento”. Tese (Título de Doutor em Engenharia), Escola Politécnica, Universidade de São Paulo, São Paulo, p. 209.
Yu, T. et al. (2010), Finite element modeling of confined concrete-II: Plastic-damage model. Engineering Structures, v. 32, n. 3, p. 680-691. https://doi.org/10.1016/j.engstruct.2009.11.013
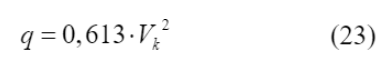
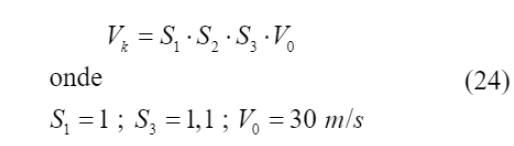

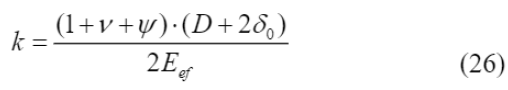

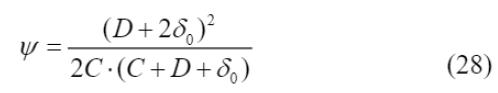
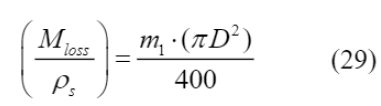
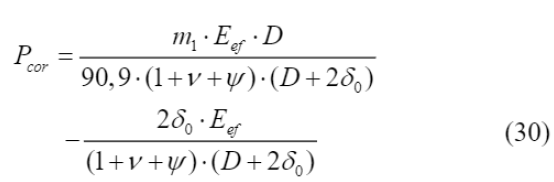

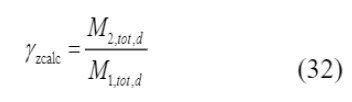
Quadro 1. Resumo de análises realizadas
Análise
Características
AN1
Análise linear física e geométrica, com redução de 20% do módulo de elasticidade
LF, LG e 0.8E
AN2
Análise linear física, não linear geométrica, com redução de 20% do módulo de elasticidade
LF, NLG e 0.8E
AN3
Análise não linear física e geométrica, sem redução do módulo de elasticidade
NLF, NLG e E
AN4 a AN11
Análise não linear física e geométrica, sem redução do módulo de elasticidade, com adição da corrosão
NLF, NLG, E e corrosão
Tabela 2. Resumo de parâmetros utilizados nas simulações
Análise
C20 e C30
C40 e C50
m1 [%]
RDeslocamento radial, δc [μm]
Mloss [g/m]
m1 [%]
Deslocamento radial, δc [μm]
Mloss [g/m]
3 barras
AN3
0.091
0.00
3.51
0.091
0.00
3.51
AN4
0.150
8.13
5.79
0.300
28.75
11.57
AN5
0.200
15.00
7.72
0.350
35.63
13.50
AN6
0.250
21.88
9.65
0.400
42.51
15.43
AN7
0.300
28.75
11.57
0.450
49.38
17.36
5 barras
AN3
0.091
0.00
3.51
0.091
0.00
3.51
AN8
0.105
1.94
4.05
0.125
4.69
4.82
AN9
0.110
2.63
4.24
0.138
6.41
5.31
AN10
0.115
3.31
4.44
0.150
8.13
5.79
AN11
0.120
4.00
4.63
0.163
9.85
6.27
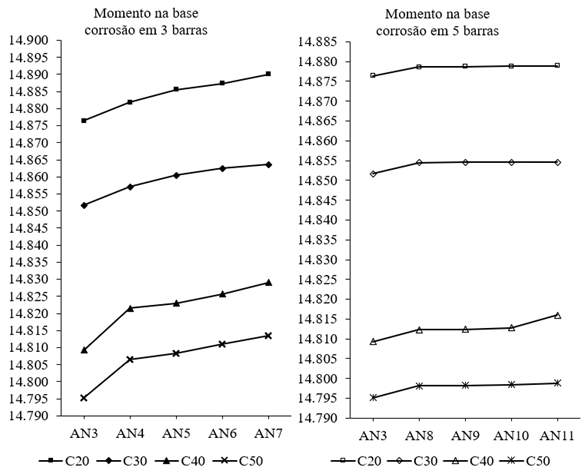
Figura 13.
Valores de momento na base da estrutura para as análises estudadas
Tabela 3. Coeficiente γzcalc
Análise
Características
AN1
Análise linear física e geométrica, com redução de 20% do módulo de elasticidade
LF, LG e 0.8E
AN2
Análise linear física, não linear geométrica, com redução de 20% do módulo de elasticidade
LF, NLG e 0.8E
AN3
Análise não linear física e geométrica, sem redução do módulo de elasticidade
NLF, NLG e E
AN4 a AN11
Análise não linear física e geométrica, sem redução do módulo de elasticidade, com adição da corrosão
NLF, NLG, E e corrosão
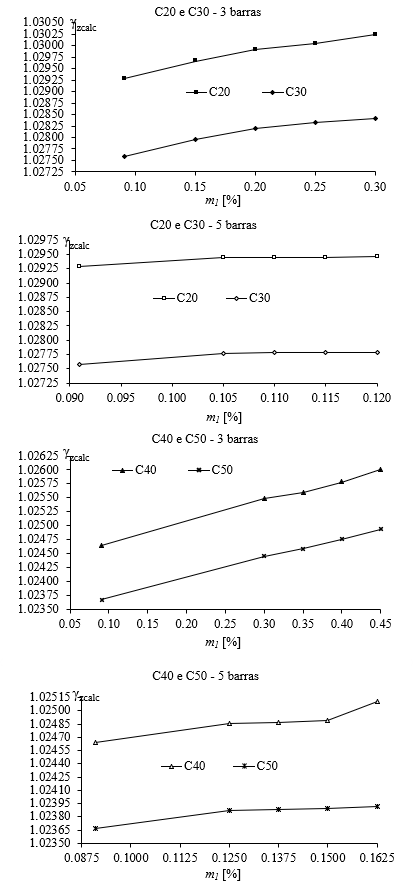
Figura 14.
Relação entre m
1
e o coeficiente γ
zcalc
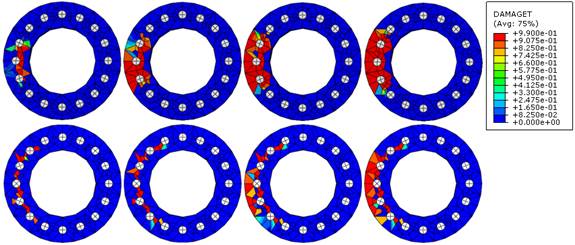
Figura 15.
Evolução do dano na estrutura em AN7 e AN11 com o concreto C40