| Investigación Básica | https://doi.org/10.21041/ra.v12i2.570 |
Análisis de la influencia de la variación de excentricidad de tendones no-adherentes en el comportamiento estructural de losas planas postensadas
Numerical analysis of the effect of variation of eccentricity of unbonded post-tensioned tendons on the structural behavior of flat slabs Análise da influência da variação da excentricidade de cordoalhas engraxadas no comportamento estrutural de lajes lisas protendidas
Rogério Cattelan
Antocheves de Lima1
*
![]() ,
Luciano
Cielo1
,
Luciano
Cielo1
![]() ,
André
Lübeck1
,
André
Lübeck1
![]() ,
Almir
Barros da Silva Santos Neto1
,
Almir
Barros da Silva Santos Neto1
![]()
1 Universidade Federal de Santa Maria, Av. Roraima nº 1000 Cidade Universitária Bairro - Camobi, Santa Maria - RS, 97105-900, Brazil.
*Contact author: rogerio@ufsm.br
Recepción:
11
de
noviembre
de
2021.
Aceptación:
26
de
febrero
de
2022.
Publicación: 01 de mayo de 2022.
| Citar como:Cattelan, R., Cielo, L., Santos Lübeck, A., Neto, A. B. S. (2022), "Análisis de la influencia de la variación de excentricidad de tendones no-adherentes en el comportamiento estructural de losas planas postensadas", Revista ALCONPAT, 11 (2), pp. 210–226, DOI: https://doi.org/10.21041/ra.v12i2.570 |
Resumen
En este estudio se evaluó la influencia de las variaciones de excentricidad de los cables en modelos con losas planas postensadas. El correcto posicionamiento de los tendones en el montaje de losas planas postensadas es fundamental para que el sistema estructural logre un adecuado rendimiento y seguridad. Se analizaron cuatro modelos arquitectónicos diferentes con modificación de la altura de los cables en diferentes puntos y cantidad. Se evaluaron tensiones de pre compresión, tensiones extremas en el tope y base, desplazamientos verticales, balanceo de carga y cantidad de acero pasivo de las losas. Para el análisis se utilizó el software ADAPT Floor Pro. El proyecto sigue las recomendaciones de la NBR 6118:2014 y ACI 318:2019. Para los modelos evaluados, se encontró que la variación en la excentricidad vertical de los tendones en la base de la losa reduce aún más los valores de las tensiones aplicadas, en comparación con la variación en el tope.
Palabras clave:
hormigón postensado,
postensión no-adherente,
excentricidad de los tendones,
Concreto Protendido
1. IntroducciÓn
El uso de postensión con los tendones no-adherentes en construcciones es muy utilizada en países económicamente desarrollados, tales como Estados Unidos y Australia. Se puede también mencionar regiones del Medio Oriente, Sudeste de Asia y Reino Unido, así como algunos países de América del Sur, en razón del excelente rendimiento estructural y de los beneficios económicos (Aalami, 2000; Santos, 2017; Silva et al., 2018).
La implementación de este sistema de postensión solo fue incluida en la norma del American Concrete Institute (ACI) 318 en 1963, después de la realización de diversas obras por el mundo (Aalami, 2000; Kang and Bondy, 2008). En Brasil, el uso de losas planas con postensión no-adherente se inició solo en el año 1997 (Carvalho, 2017). Proyectos arquitectónicos que proponen grandes espacios, con reducido número de columnas y vigas, principalmente en construcciones y residencias de alto nivel, impulsó el uso de losas con postensión no-adherente en el país (Santos, 2017; Almeida, 2001; Loureiro, 2006). Se puede también citar el desarrollo de acero de alta resistencia, juntamente con la evolución de softwares de calibración, además de la practicidad de ejecución del sistema, como factores decisivos para el avance en la aplicación efectiva de la postensión en la construcción civil (Carvalho, 2017; Loureiro, 2006).
Además del beneficio financiero, la postensión trae mejorías en el desempeño en el Estado Límite de Servicio (ELS) y en la seguridad de las estructuras de hormigón, con énfasis para la durabilidad, pues la ausencia o reducción de las grietas garantiza una protección más grande de las armaduras, inhibiendo el fenómeno de la corrosión (NBR 6118, 2014; Cholfe y Bonilha, 2018; Silva, 2003).
En las losas planas con postensión no-adherente, los tendones son, en la mayoría de las veces, con dibujos en formato parabólico, resultando en excentricidades con relación al centro de la losa, que permiten aumentar la eficiencia de las fuerzas aplicadas por los cables, aumentando también la capacidad de balanceo de las cargas (Pfeil, 1984; Vicente y Albino, 1994). El concepto de carga balanceada tiene como principio básico propiciar que las cargas verticales equivalentes de la postensión mantengan en balanceo una fracción de las cargas permanentes actuantes, quedando la estructura, para ese nivel de cargamento, sometida solo a tensiones de compresión (Silveira, 2002; Aalami, 1990; Aalami y Bommer, 1999).
Este factor apunta la necesidad de que el montaje de los tendones sea el más próximo posible de las posiciones verticales indicadas en el proyecto, pues un posicionamiento vertical incorrecto puede ocasionar el surgimiento de manifestaciones patológicas, flechas distintas de las previstas en el proyecto o mismo, en situaciones más extremas, el colapso de la estructura (Silva et al., 2018; Aalami y Bommer, 1999; Romanichen y Souza, 2019).
Para mantener los tendones en la posición vertical definida en proyecto, se utiliza separadores de apoyo puntuales. Estos separadores, cuando industrializados, vienen en modelos plásticos o de acero, con riguroso control en el proceso de producción de la altura. Sin embargo, excepcionalmente, se hace la producción de estos separadores en obra, con el pliegue de barras de acero, no presentando, en la mayoría de las veces, el adecuado control de la producción y, en consecuencia, una variabilidad en sus alturas (Loureiro, 2006; Aalami, 2014). Además de eso, otras situaciones, como la falta de atención en el manejo con la armadura, junto con los daños causados en las operaciones de hormigonado, pueden causar el rompimiento o dislocamiento de estos separadores (Figura 1).
Todavía, aunque haya el control y el cuidado con relación a los aspectos apuntados anteriormente, hay también el error humano en el posicionamiento de estos separadores durante la etapa del montaje de los tendones. Tales circunstancias pueden producir un posicionamiento vertical de los tendones, con una altura y excentricidad distintas del valor especificado por el proyectista.
Los problemas provenientes del mal posicionamiento de los tendones pueden estar relacionados con el surgimiento de situaciones como fisura de la losa, desplazamientos verticales excesivos, tensiones actuantes distintas de las calculadas en proyecto, superando los límites de tracción o compresión del hormigón en el elemento estructural. Aún se puede mencionar desplazamiento del hormigón en función de menores cubrimientos y la aceleración en el proceso de corrosión del acero a causa de falta de cubrimiento (Souza, 2018; Xin y Xianyan, 2012).
 |
||||
| Figura 1. Operación de hormigonado: (a) Manejo de la mano de obra en contacto con la armadura. (b) Separador dañado y mal posicionado. | ||||
El principal factor influyente para el desempeño del sistema es el respecto por el correcto posicionamiento vertical de los cables especificado en el proyecto durante la etapa de montaje (Carvalho, 2017; Souza Junior y Oliveira, 2016; Caro et al., 2013).
Cauduro (2002) recomienda que desvíos verticales en la posición de los tendones sean toleradas hasta +/- 5mm, en losas que no excedan el espesor de 200 mm y tolerancia máxima de +/- 10 mm, en losas con espesor entre 200 mm y 600 mm. Además de eso, el autor también señala que los puntos altos y bajos son las posiciones más críticas y que la posición horizontal de los tendones no es crucial, sin embargo, se debe evitar oscilaciones excesivas. Así, los valores aceptables de desvíos absolutos que independen de la geometría de la estructura y esfuerzos involucrados pueden resultar en inseguridad en la evaluación estructural. Las variaciones de excentricidad de los cables de postensión pueden ser más o menos influyentes, dependiendo del espesor de la losa, o sea, el error relativo de excentricidad, espacio entre apoyos y cargamento aplicado.
En ese estudio se evaluó la influencia de variaciones de excentricidad de los cables en losas planas de postensión. Se desarrolló modelos variando los espesores y espacios de las losas, además del error relativo de excentricidad del cable. El dimensionamiento de las losas planas de hormigón postensados siguió las especificaciones de la ABNT NBR 6118:2014 y algunas recomendaciones del ACI 318:2019.
2. MetodologÍa
2.1 Geometría de las Losas y Trazo de los Cables
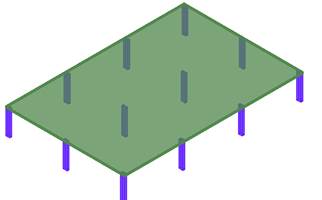
Los modelos estructurales probados son compuestos por un piso de losa, apoyada directamente en las columnas, sin la existencia de vigas, como en la Figura 2. Los espacios entre las columnas son iguales en cada modelo y tienen variaciones de 7,0 a 10,0 m, resultando en cuatro modelos estructurales, con espacios de 7,0 m x 7,0 m hasta 10,0 x 10,0 m, variando de metro en metro, y los modelos son nombrados de M7, M8, M9 e M10.
Los modelos estructurales presentan distintos espesores de losas, definidos aproximadamente por la relación L/42 (ACI 318, 2019), donde L es el vano de la losa. En la Tabla 1 se presentan los modelos estructurales con sus nomenclaturas, vanos entre columnas y los espesores para cada una de las losas.
El trazo de los cables de postensión siguió la premisa de disponer las fajas de tendones concentradas en la dimensión más grande de la losa (dirección x) y, tendones distribuidos en la dirección perpendicular (dirección y), Figura 3.
 |
||||
| Figura 2. Modelo estructural del piso para los análisis. | ||||
| Tabla 1. Nomenclatura y dimensiones de los modelos estructurales. | ||||||||||||||
| Nomenclatura | Espacio entre columnas | Espesor de la losa | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Modelo | M7 | 7,0 m x 7,0 m | 170 mm | |||||||||||
| M8 | 8,0 m x 8,0 m | 190 mm | ||||||||||||
| M9 | 9,0 m x 9,0 m | 210 mm | ||||||||||||
| M10 | 10,0 m x 10,0 m | 240 mm | ||||||||||||
 |
||||
| Figura 3. Layout de los tendones no-adherentes en la losa plana postensado. | ||||
Se analizó, exclusivamente, la faja central de tendones de la dirección x, pues en esta faja se concentran los cargamentos más grandes y, así, es más influenciada por las variaciones de excentricidad aplicadas en cada modelo propuesto.
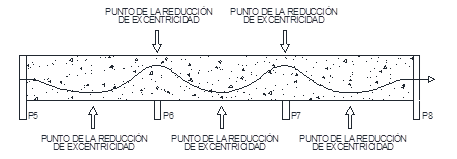
Las variaciones de las excentricidades fueron probadas sobre las columnas (cumbre) y en el centro de los espacios (base), de manera aislada y también conjunta, según el esquema de la Figura 4. En el primer caso fueron reducidas las excentricidades de los tendones solamente en la parte superior de la losa (cumbre), en las regiones de las columnas P6 y P7. Después, se disminuyó la excentricidad en las regiones entre los apoyos, en la parte inferior de la losa (base). En el tercero caso, se realizó el análisis con variaciones en conjunto, denominada como combinación crítica, reduciendo las excentricidades de los tendones simultáneamente en las regiones entre los apoyos y también en el tope de las columnas P6 y P7.
 |
||||
| Figura 4. Puntos de reducción de la excentricidad para las losas. | ||||
Para cada uno de los cuatro modelos (Tabla 1) se desarrolló cuatro hipótesis de variaciones de excentricidades, con valores de 5 mm, 10 mm, 15 mm y 20 mm. Se adoptó estos valores en el estudio a causa de que, generalmente, en los proyectos, los puntos de apoyo verticales son presentados en ese formato, visando viabilizar la conferencia in loco. Además, los estudios presentados en (Cauduro, 2002) demuestran valores límites de 5 mm y 10 mm de reducción en las excentricidades de los tendones de las losas, para espesores de losas iguales o más grandes que las definidas en este estudio. En la Tabla 2 se presentan las hipótesis de variaciones, con sus nomenclaturas y las respectivas reducciones de las excentricidades.
El espacio entre el P5 y el P6 se lo nombró “primero” en los análisis, el espacio entre el P6 y el P7 recibió la denominación “central” y, por fin, el espacio entre el P7 y el P8 recibió la denominación de “último”, según el esquema de la Figura 5.
2.2 Materiales y Parámetros Normativos
Se consideró un cargamento variable (sobrecarga) con el valor mínimo recomendado en la (NBR 6120, 2019) para espacios de uso general de edificaciones comerciales, igual a 2,5 kN/m². Se adoptó también un cargamento permanente de revestimiento de valor igual a 1,0 kN/m². Además de estos dos cargamentos, se aplicó el peso mismo calculado en función del espesor de la losa, en cada situación.
Se adoptó el valor de 2,5 cm para cubrir las armaduras pasivas y 3,0 cm para cubrir las armaduras activas. En los modelados se adoptó hormigón clase C35, con fck de 35,0 MPa y módulo de elasticidad (E) de 39,7 GPa.
Se utilizó tendones del tipo CP 190 RB (fptk = 1900 MPa), con diámetro nominal de 12,7 mm y área de acero nominal 100,9 mm².
En los análisis de los modelos de losas se siguió inicialmente tres parámetros fundamentales normatizados: tensión de precompresión mínima, tensión nominal límite de tracción y desplazamientos verticales máximos. Después que los criterios fueron logrados, se adaptó las demás consideraciones, como el balanceo de cargas y desplazamientos finales. Después de la realización de estos primeros análisis, se dimensionó las losas para en Estadio-Límite de Servicio (ELS) y Estadio- Límite Último (ELU).
La tensión de precompresión, en cualquier punto de la losa, respetó el valor mínimo de 1,0 MPa, (ACI 318, 2019; NBR 6118, 2014). En los modelos, en el proceso de predimensionamiento, donde la precompresión de 1,0 MPa no fue suficiente para atender el límite de la máxima tensión normal de tracción en el hormigón o desplazamientos, se aumentó la calidad de tendones hasta que se alcanzó este parámetro.
Para el parámetro de balanceo de cargas, resultados entre 60% a 80% de la carga permanente, estos valores son usuales para losas de construcciones residenciales, comerciales y garajes, (Loureiro, 2006).
Para el dimensionamiento se definió la utilización de la postensión limitada, (NBR 6118, 2014). Según la norma, en los proyectos con losa plana postensada, es suficiente que se atenda el ELS-F (Estadio Límite de Servicio de Formación de Fisuras), para la frecuente combinación de las acciones, en cualquier de las clases de agresividad ambiental. El valor límite de tensión normal de compresión en el hormigón en el acto de la postensión fue limitado en 15,75 MPa y en el estadio límite de formación de fisuras 21,0 MPa, (ACI 318, 2019).
La norma (NBR 6118, 2014) limita los desplazamientos verticales, para la aceptabilidad sensorial de columnas y losas, en la relación L/250 (teniendo en cuenta que L es el espacio libre entre columnas). Se tomó este valor como límite para los modelos antes de la inserción de variaciones en las excentricidades de los tendones.
Las armaduras pasivas positivas y negativas fueron calculadas para los distintos modelos, según los criterios presentados en (NBR 6118, 2014). La Tabla 3 resume los parámetros utilizados en la verificación de las losas.
Después de la inserción de las variaciones de excentricidad, se hizo los análisis para confirmar cuales modelos se mantuvieron atendiendo a los límites y, de esa manera, calcular las armaduras pasivas y definir la posición y el valor máximo de variación aceptable de la excentricidad de los tendones.
2.3 Análisis de Dimensionamiento
Se realizó el dimensionamiento de las losas con la ayuda del programa Adapt Floor 2017 PRO. Este programa es específico para el análisis y dimensionamiento de hormigón postensado y discretiza la losa en elementos finitos de placa, verificando los efectos de la postensión según la geometría y fuerza de los tendones, en cada elemento.
El programa permite la generación automática de la malla de elementos finitos, y compete al usuario definir el tamaño de los elementos de esta malla. En este trabajo se testó dos tamaños de dimensión máxima de los elementos. Como no se encontró diferencias significativas en los resultados, se definió la utilización de una dimensión máxima para los elementos de 500 mm de malla para los análisis. La Figura 6 muestra la malla de elementos finitos para el Modelo M8.
Para el análisis de los modelos de las losas se lanzó líneas de soporte en el alineamiento de las columnas. Esas líneas permiten al programa definir “design sections”, donde son presentados al usuario los valores medios de las tensiones en la losa. Así, las tensiones son analizadas a partir de las regiones tributarias que compilan los resultados de las áreas definidas por las líneas de soporte.
La cantidad de tendones para la faja dimensionada, para los Modelos M7, M8, M9 e M10 fueron 10, 17, 25 y 33 unidades, respectivamente.
En la Figura 7 se presentan las tensiones normales en la dirección “x” para las faces superior e inferior de la losa, para la combinación frecuente, del Modelo M8.
3. DiscusiÓn de los resultados
3.1 Tensiones de precompresión
La Tabla 4 presenta los resultados para los valores de las tensiones normales de precompresión en las losas. Las tensiones normales de precompresión no varían en función de la modificación de la posición vertical de los tendones y sí en virtud de la cantidad de tendones y de la intensidad de la fuerza aplicada por ellos. Una mayor densidad de tendones, necesaria para equilibrar los modelos con espacios mayores, resultó en valores mayores de tensión de precompresión. Para el modelo M7, las tensiones variaron entre 1,0 y 1,11 MPa, entre espacios. Mientras que para el modelo M10 variaron entre 1,43 y 1,60 MPa, entre espacios.
3.2 Tensiones normales máximas en las losas
Las tensiones normales de tracción en la faz inferior de la losa (Tabla 5), para los cuatro modelos, incluso con los cambios en el posicionamiento vertical de las excentricidades de los tendones, recibieron el valor límite máximo de 3,38 MPa en el ELS-F, conforme establecido en la (NBR 6118, 2014).
En los modelos de referencia, en la sección del espacio central, se encontraron tensiones de compresión en la faz inferior de la losa, debido a una mayor fuerza de postensado en esta sección con respecto al primer y último espacio.
Al modificar las excentricidades de los tendones, exclusivamente en el tope de las columnas, los esfuerzos sufren menores variaciones en comparación con las reducciones de tensiones provocadas en los modelos con variaciones de excentricidades en la base. Las reducciones de las excentricidades en la combinación crítica son más desfavorables. Aun así, en todas las hipótesis las tensiones normales de tracción en la faz inferior de la losa permanecieron dentro del límite de 3,38 MPa (NBR 6118, 2014). Los análisis de las tensiones en la faz superior están resumidos en la Tabla 6. Se destacaron en amarillo las tensiones que excedieron el límite normativo. La variación de la excentricidad en el tope de las columnas, en la hipótesis H5, fueron las únicas que presentaron resultados normales de tensión de tracción en la faz superior, atendiendo al límite normativo de 3,38 MPa, (NBR 6118, 2014). La reducción de excentricidad en la faz inferior de la losa genera mayores tensiones normales de tracción en la faz superior del elemento, en la región de apoyo (columnas), en comparación con la variación de excentricidad en la faz superior. Los modelos M7 y M9 fueron los únicos que, en la hipótesis H5 de modificación de los valores de excentricidad del caso “Base”, tuvieron sus valores de tensión normal de tracción inferiores a 3,38 MPa.
Además, en la combinación crítica, en ninguna de las variaciones de excentricidad, las tensiones normales de tracción obtenidas fueron menores al límite normativo establecido de 3,38 MPa, para el ELS en la combinación frecuente, (NBR 6118, 2014).
3.3 Desplazamientos verticales
En la Tabla 7 se presentan los valores obtenidos para los desplazamientos verticales diferidos de las losas.
Los modelos M7 y M8 presentaron, para todas las hipótesis y casos de variaciones, valores de desplazamientos verticales con límites de 28,0 mm y 32,0 mm, respectivamente. El modelo M9, solo en el espacio central, obtuvo valores menores a 36,0 mm de desplazamientos verticales. Finalmente, el modelo M10 tuvo sus valores de desplazamiento vertical por debajo de 40,0 mm, límite normativo (NBR 6118, 2014), en todas las variaciones de excentricidades para el caso “Tope” de modificaciones en las alturas de los tendones.
Para mejor comprensión de los efectos de la alteración de la excentricidad de los cables en el comportamiento a flexión de la losa, se desarrolló el gráfico de la Figura 8. En este gráfico en el eje de ordenadas, la relación f/L representa, en forma de denominador de fracción, la flecha equivalente, por ejemplo L/430, donde el valor L/250 es la flecha límite. En el eje de abscisas se sitúan las excentricidades relativas, o sea, el valor del desplazamiento dado al cable (excentricidad), en relación al espesor de la losa. La excentricidad relativa (o variación de excentricidad relativa) puede ser más o menos influyente para diferentes casos. Observando la alineación de los puntos, puede verse que para todos los modelos de losa la hipótesis crítica conduce a mayores variaciones en los desplazamientos. Se han insertado líneas discontinuas para demostrar los casos probados, M7 a M10.
Para los casos M9 y M10, la posición de la excentricidad, superior, inferior o crítica, fue menos influyente que para los casos M7 y M8. La amplitud de variación de las flechas aumentó cuando se acrecentó la excentricidad relativa. Para el caso M9 -crítico, el aumento de la excentricidad relativa de 2,4 % a 9,5 % resultó en un aumento de la flecha de L/248 a L/230. Para el caso M7 - crítico, un aumento en la excentricidad relativa de 2,9% a 11,8% resultó en un aumento de la flecha de L/363 a L/325.
3.4 Balanceo de cargas
Los valores del balanceo de cargas aumentan a partir de la inserción de tendones impuestas para cumplir con los límites de tensiones normales de tracción en las faces inferior, superior y de precompresión de la losa. La Tabla 8 muestra el resumen de los valores del balanceo de carga para todos los conjuntos evaluados.
Solamente el modelo M7 cumplió con las recomendaciones de (Loureiro, 2006; Aalami, 2014), para valores de balanceo de cargas, entre 60% y 80%. En los demás modelos, el balanceo varió entre el 59 y el 95% de las cargas permanentes.
3.5 Armaduras pasivas
En la Tabla 9 se presentan los resultados del cálculo de las armaduras pasivas positivas.
Para las variaciones en las hipótesis H5 en el caso “Tope”, las tasas de armaduras pasivas positivas se mantuvieron iguales a sus respectivos modelos de referencia. Los cambios en la tasa de armaduras ocurrieron en los mismos modelos, pero en diferentes tramos. La Tabla 10 muestra los cálculos de las armaduras para combatir la flexión negativa en el caso H5.
La tasa de armadura pasiva, para combatir la flexión negativa, se mantuvo igual para los modelos de hipótesis de referencia en comparación con los modelos en la hipótesis H5 de variación de excentricidad para el caso "Tope". Esto porque la reducción de 5 mm en la altura de las excentricidades de los tendones, colocadas encima de las columnas, no presentó suficientes nuevos esfuerzos para aumentar la cantidad de acero en este caso.
La variación de la excentricidad de los tendones en la faz inferior para el modelo M7 obligó a aumentar la tasa de refuerzo para combatir la flexión negativa de las columnas, en relación al modelo de referencia, para la misma distancia entre columnas analizada.
4. Conclusiones
En este trabajo se realizó el análisis y diseño de cuatro modelos de losas planas postensadas, con variación de espacios y excentricidades de los tendones, con el fin de simular posibles errores de montaje en el posicionamiento de los espaciadores de apoyo vertical. En los diferentes modelos se analizaron los esfuerzos de precompresión, tensiones normales en las faces inferior y superior de la losa, balanceo de carga y desplazamientos verticales. También se dimensionaron las armaduras pasivas positivas y negativas.
Por medio del análisis de los resultados, es posible concluir que la reducción en las excentricidades de los tendones interfirió directamente en las tensiones de las losas planas postensadas, provocando principalmente reducciones en la porción de tensiones normales combatidos por el postensado. La disminución de la excentricidad de los tendones en la faz inferior de la losa interfiere negativamente en mayor medida que la variación de la excentricidad en la faz superior, afectando el control de las tensiones normales en la losa, así como en los criterios de balanceo de cargas y desplazamientos.
El modelo M7 fue el único que obtuvo valores para los criterios analizados, cumpliendo con los límites normativos, con variaciones de las excentricidades en la hipótesis H5, para los casos “Tope” y “Base”, con la posición de la variación de las alturas de los tendones.
Por otro lado, los Modelos M8, M9 y M10, solo en la variación para la hipótesis H5, en el caso “Tope”, presentaron resultados de tensiones normales de tracción por debajo del límite de 3,38 MPa, establecido por la norma (NBR 6118, 2014).
El factor responsable de las tensiones de precompresión en el elemento estructural fue únicamente la cantidad de tendones y el esfuerzo aplicado sobre los mismos, sin sufrir reducciones en los valores por la modificación vertical del posicionamiento.
Los desplazamientos verticales en las losas sufrieron cambios con la aplicación de variaciones en las excentricidades. Los modelos M7 y M8 fueron los únicos que se mantuvieron por debajo de los límites normativos de L/250 para todas las hipótesis de variaciones de excentricidades aplicadas.
El criterio de balanceo de carga siguió cumpliendo con los límites recomendados solo en el modelo M7. Al ser criterios complementarios, no estandarizados, pueden aceptarse en el diseño, incluso con valores no recomendados.
Las tasas de armadura pasiva positiva y negativa se mantuvieron iguales, solo en los modelos de referencia y en la hipótesis H5 de variación de la excentricidad del caso “Tope”.
La máxima variación relativa de la excentricidad para que los criterios analizados sigan cumpliendo los límites establecidos es de 2,1% al comparar la variación de la excentricidad con el espesor de la losa, en el caso “Tope”, para cumplir el criterio.
En el análisis se puede afirmar que es admisible, para losas planas postensadas con postensado no adherente, del tipo CP 190 RB ( 12,7 mm, con espacios entre columnas de 7,0 m a 10,0 m, una tolerancia máxima de 5mm de reducción en el posicionamiento vertical de los cables en la faz superior. Este análisis es más limitado cuando se compara con las tolerancias encontradas en la literatura.
Referencias
Aalami, B. O. (1990), Load Balancing: A Comprehensive Solution to Post - Tensioning. ACI Structural Journal: 662-670.
Aalami, B. O. (2014), “Post-Tensioned Manual”. California: ADAPT, v.1, p. 500.
Aalami, B. O. (2000),
Structural Modeling of Post-Tensioned Members. Journal of Structural Engineering. Vol. 126 Nº. 2: 157-162.
Aalami, B. O., Bommer, A. (1999), “Design Fundamntals of Post-Tensioned Concrete Floors”. Post-Tensioning Institute (PTI), Farmington Hills, USA.
Almeida, S. R. M. (2001), “Contribuição ao projeto ótimo de cabos em vigas de concreto protendido”. Tese de Doutorado. Pontifícia Universidade Católica do Rio de Janeiro. https://doi.org/10.17771/PUCRio.acad.2058.
American Concrete Institute (2019). ACI 318 - Building Code Requirements for Structural Concrete. Farmington Hills, MI.
Associação Brasileira de Normas Técnicas. (2019). NBR 6120: Ações para o cálculo de estruturas de edificações. Rio de Janeiro.
Associação Brasileira de Normas Técnicas. (2014). NBR 6118: Projeto de estruturas de concreto - Procedimento. Rio de Janeiro.
Caro, L. A., Vargas, J. R. M., Ros, P. S. (2013), Prestress losses evaluation in prestressed concrete prismatic specimens. Engineering Structures. Vol. 48, p. 704-715. https://doi.org/10.1016/j.engstruct.2012.11.038.
Carvalho, R. C. (2017), “Estruturas em concreto protendido: cálculo e detalhamento”. Ed. Pini. São Paulo, Brasil, p. 448.
Cauduro, E. L. (2002), “Manual para a boa execução de estruturas protendidas usando cordoalhas de aço engraxadas e plastificadas”. São Paulo, Brasil.
Cavaco, E. S., Bastos, A., Santos, F. A. (2017), “Effects of corrosion on the behaviour of precast concrete floor systems”. Journal Construction and Building Materials. N. 145: 411-418. https://doi.org/10.1016/j.conbuildmat.2017.04.044.
Cholfe, L., Bonilha, L. (2018), “Concreto protendido: teoria e prática”. Oficina de Textos. São Paulo, Brasil, p. 360.
Hanai, J. B. (2005), “Fundamentos do Concreto Protendido”. E-book. São Carlos.
Kang, T., Bondy, K. B. (2008), Recommendations for Design of Post-Tensioned Slab-Column Connections Subjected to Lateral Loading. PTI Journal, Post Tensioning Institute. Vol. 6, nº 1.
Loureiro, G. J. (2006), Projeto de Lajes Protendidas com Cordoalhas Engraxadas. Revista Ibracon de Estruturas e Materiais, ed. 44.
Pfeil, W. (1984), “Concreto Protendido - Introdução”. LTC. Rio de Janeiro.
Romanichen, R. M., Souza, R. A. (2019), Reinforced concrete corbels strengthened with external prestressing. Revista Ibracon de Estruturas e Materiais. V. 12. N. 4, p. 812 - 831. https://doi.org/10.1590/S1983-41952019000400006.
Santos, J. S. D. (2017), “Desconstruindo o Projeto Estrutural de Edifícios: Concreto Armado e Protendido”. 1ª. ed. São Paulo: Oficina de Textos. p. 127.
Silva, G., Prata, B., Albuquerque, A. (2018), Análise da eficiência dos sistemas estruturais para edifícios em concreto. Ambiente Construído. Vol. 18, n. 1, p. 313-325. https://doi.org/10.1590/s1678-86212018000100223.
Silva, R.C. (2003), “Vigas de concreto armado com telas soldadas: análise teórica e experimental da resistência à força cortante e do controle da fissuração”. Tese de doutorado. Escola de Engenharia de São Carlos, Universidade de São Paulo. p. 328.
Silveira, M. C. A. (2002). “Práticas de Projeto e Execução de Edificações Protendidas com Cordoalhas Engraxadas e Plastificadas”. Revista Ibracon de Estruturas e Materiais. 44º Congresso Brasileiro do Concreto. Belo Horizonte.
Souza, F. A. (2018), “Radier simples, armado e protendido - Teoria e Prática”. Editora Catarse. São Paulo, Brasil, p. 312.
Souza Junior, O. A., Oliveira, D. R. C. (2016), “Influence of the tendon´s layout on the shearing resistance of prestressed concrete beams”. Revista Ibracon de estruturas e materiais. Vol. 9, N. 5. p. 765 - 795. https://doi.org/10.1590/S1983-41952016000500008.
Vicente, C. M. D. S., Albino, J. P. D. C. (1994), “Lajes em Concreto Armado e Protendido”. Editora da Universidade Federal Fluminense. Rio de Janeiro, Brasil, p. 584.
Xin, F., Xianyan, Z. (2012). “Experimental research on crack width of retard bonded partially prestressed concrete beams”. International Conference on Advances in Civil Infrastructure Engineering. Hunan.
Tabla 2. Hipótesis de las variaciones de excentricidades.
Hipótesis
Nomenclatura
Reducción de excentricidad (mm)
Referencia
H0
0
Hipótesis 1
H5
5
Hipótesis 2
H10
10
Hipótesis 3
H15
15
Hipótesis 4
H20
20
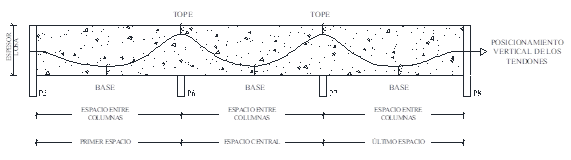
Figura 5.
Posicionamiento vertical de los tendones en la losa.
Tabla 3. Criterios analizados con los límites y respectivas fuentes indicadas.
Criterio analizado
Límite
Parámetro
Unidad
Fuente
Tensión de precompresión
Mínimo
1,0
MPa
NBR 6118, 2014 e ACI 318, 2019
Tensión de tracción en las faces inferior y superior
Máximo
3.38
MPa
NBR 6118, 2014
Tensión de compresión máxima para el Acto de la Postensión
Máximo
15,0
MPa
ACI 318, 2019
Tensión de compresión máxima para el ELS-F
Máximo
21,0
MPa
ACI 318, 2019
Balanceo de cargas
Recomendação
60 a 80
%
Loureiro, 2006 e Hanai, 2005
Desplazamientos verticales diferidos
Máximo
L/250
-
NBR 6118, 2014
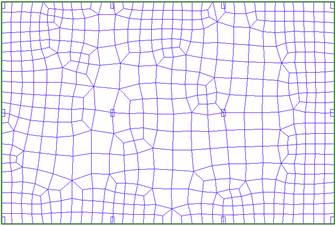
Figura 6.
Malla de elementos finitos de la losa.
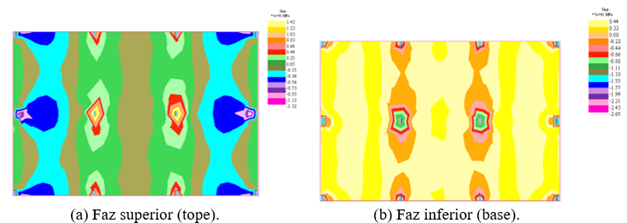
Figura 7.
Tensiones normales (dirección x), para combinación frecuentes, de la loza modelo M8, en MPa.
Tabla 4. Verificación de las tensiones de precomprensión en las losas (valores en MPa).
Modelo
M7
Caso
Referencia
Tope
Base
Crítico
Hipótesis
H5
H10
H15
H20
H5
H10
H15
H20
H5
H10
H15
H20
Espacio entre columnas
Primero
1
1
1
1
1
1
1
1
1
1
1
1
1
Central
1,11
1,11
1,11
1,11
1,11
1,11
1,11
1,11
1,11
1,11
1,11
1,11
1,11
Último
1,01
1,01
1,01
1,01
1,01
1,01
1,01
1,01
1,01
1,01
1,01
1,01
1,01
Modelo
M8
Caso
Referencia
Tope
Base
Crítico
Hipótesis
H5
H10
H15
H20
H5
H10
H15
H20
H5
H10
H15
H20
Espacio entre columnas
Primero
1,27
1,27
1,27
1,27
1,27
1,27
1,27
1,27
1,27
1,27
1,27
1,27
1,27
Central
1,36
1,36
1,36
1,36
1,36
1,36
1,36
1,36
1,36
1,36
1,36
1,36
1,36
Último
1,31
1,31
1,31
1,31
1,31
1,31
1,31
1,31
1,31
1,31
1,31
1,31
1,31
Modelo
M9
Caso
Referencia
Tope
Base
Crítico
Hipótesis
H5
H10
H15
H20
H5
H10
H15
H20
H5
H10
H15
H20
Espacio entre columnas
Primero
1,53
1,53
1,53
1,53
1,53
1,53
1,53
1,53
1,53
1,53
1,53
1,53
1,53
Central
1,75
1,75
1,75
1,75
1,75
1,75
1,75
1,75
1,75
1,75
1,75
1,75
1,75
Último
1,53
1,53
1,53
1,53
1,53
1,53
1,53
1,53
1,53
1,53
1,53
1,53
1,53
Modelo
M10
Caso
Referencia
Tope
Base
Crítico
Hipótesis
H5
H10
H15
H20
H5
H10
H15
H20
H5
H10
H15
H20
Espacio entre columnas
Primero
1,43
1,43
1,43
1,43
1,43
1,43
1,43
1,43
1,43
1,43
1,43
1,43
1,43
Central
1,6
1,6
1,6
1,6
1,6
1,6
1,6
1,6
1,6
1,6
1,6
1,6
1,6
Último
1,5
1,5
1,5
1,5
1,5
1,5
1,5
1,5
1,5
1,5
1,5
1,5
1,5
Tabla 5. Verificación de análisis de las tensiones normales en la faz inferior en las losas (valores en MPa).
Modelo
M7
Caso
Referencia
Tope
Base
Crítico
Hipótesis
H5
H10
H15
H20
H5
H10
H15
H20
H5
H10
H15
H20
Espacio entre columnas
Primero
2,37
2,39
2,42
2,45
2,47
2,45
2,54
2,63
2,72
2,48
2,6
2,71
2,83
Central
-0,15
-0,12
0,00
0,05
0,12
-0,10
0,00
0,02
0,05
-0,03
0,09
0,22
0,36
Último
2,52
2,55
2,58
2,60
2,63
2,61
2,69
2,78
2,86
2,63
2,75
2,86
2,97
Modelo
M8
Caso
Referencia
Tope
Base
Crítico
Hipótesis
H5
H10
H15
H20
H5
H10
H15
H20
H5
H10
H15
H20
Espacio entre columnas
Primero
2,52
2,55
2,71
2,74
2,77
2,66
2,76
2,87
2,98
2,68
2,83
2,97
3,12
Central
-0,62
-0,50
-0,50
-0,40
-0,30
-0,60
-0,50
-0,40
-0,40
-0,50
-0,30
-0,20
0,01
Último
2,48
2,51
2,54
2,57
2,61
2,58
2,69
2,79
2,90
2,62
2,75
2,89
3,03
Modelo
M9
Caso
Referencia
Tope
Base
Crítico
Hipótesis
H5
H10
H15
H20
H5
H10
H15
H20
H5
H10
H15
H20
Espacio entre columnas
Primero
2,64
2,65
2,71
2,74
2,77
2,66
2,76
2,87
2,98
2,68
2,83
2,97
3,12
Central
-1,49
-1,4
-1,3
-1,2
-1,1
-1,3
-1,2
-1,1
-1,0
-1,2
-1,0
-0,8
-0,6
Último
2,63
2,66
2,72
2,74
2,78
2,67
2,79
2,9
3,01
2,71
2,82
3,01
3,16
Modelo
M10
Caso
Referencia
Tope
Base
Crítico
Hipótesis
H5
H10
H15
H20
H5
H10
H15
H20
H5
H10
H15
H20
Espacio entre columnas
Primero
2,70
2,73
2,77
2,80
2,83
2,81
2,91
3,01
3,12
2,84
2,97
3,10
3,24
Central
-1,41
-1,33
-1,24
-1,15
-1,07
-1,34
-1,27
-1,20
-1,13
-1,26
-1,10
-0,93
-0,77
Último
2,69
2,73
2,76
2,79
2,82
2,80
2,90
3,01
3,11
2,83
2,97
3,10
3,24
Tabla 6. Verificación del análisis de las tensiones superior en las losas (valores en MPa).
Modelo
M7
Caso
Referencia
Tope
Base
Crítico
Hipótesis
H5
H10
H15
H20
H5
H10
H15
H20
H5
H10
H15
H20
Espacio entre columnas
P5
3,04
3,12
3,21
3,29
3,37
3,15
3,25
3,36
3,46
3,23
3,42
3,61
3,80
P6
3,26
3,33
3,41
3,48
3,56
3,36
3,45
3,55
3,65
3,43
3,61
3,78
3,96
Modelo
M8
Caso
Referencia
Tope
Base
Crítico
Hipótesis
H5
H10
H15
H20
H5
H10
H15
H20
H5
H10
H15
H20
Espacio entre columnas
P5
3,28
3,38
3,47
3,56
3,65
3,40
3,52
3,65
3,77
3,50
3,71
3,93
4,14
P6
3,08
3,18
3,28
3,37
3,47
3,21
3,33
3,46
3,58
3,30
3,53
3,75
3,97
Modelo
M9
Caso
Referencia
Tope
Base
Crítico
Hipótesis
H5
H10
H15
H20
H5
H10
H15
H20
H5
H10
H15
H20
Espacio entre columnas
P5
3,09
3,19
3,29
3,40
3,51
3,24
3,34
3,42
3,55
3,26
3,49
3,72
3,95
P6
3,13
3,22
3,31
3,45
3,53
3,29
3,42
3,56
3,57
3,39
3,64
3,88
4,12
Modelo
M10
Caso
Referencia
Tope
Base
Crítico
Hipótesis
H5
H10
H15
H20
H5
H10
H15
H20
H5
H10
H15
H20
Espacio entre columnas
P5
3,28
3,37
3,47
3,56
3,66
3,40
3,52
3,65
3,77
3,50
3,71
3,93
4,15
P6
3,23
3,32
3,42
3,52
3,65
3,33
3,47
3,65
3,77
3,45
3,67
3,88
4,11
Tabla 7. Análisis de los desplazamientos verticales en las losas (valores en mm).
Modelo
M7
Caso
Referencia
Tope
Base
Crítico
Hipótesis
H5
H10
H15
H20
H5
H10
H15
H20
H5
H10
H15
H20
Espacio entre columnas
Primero
18,5
18,8
19,0
19,2
19,4
19,1
19,6
20,1
20,7
19,3
20,0
20,8
21,5
Central
5,4
5,8
6,3
6,6
7,0
5,7
6,0
6,3
6,6
6,1
6,9
7,5
8,2
Último
19,1
19,3
19,4
19,6
19,8
19,6
20,1
20,6
21,1
19,8
20,4
21,1
21,8
Modelo
M8
Caso
Referencia
Tope
Base
Crítico
Hipótesis
H5
H10
H15
H20
H5
H10
H15
H20
H5
H10
H15
H20
Espacio entre columnas
Primero
24,2
24,4
24,7
24,9
25,2
24,9
25,6
26,3
27,0
25,1
26,1
27,2
28,0
Central
4,8
5,1
5,5
6,5
7,1
5,3
5,6
6,1
7,1
5,8
6,7
7,7
8,7
Último
23,9
24,2
24,6
24,8
25,1
24,7
25,5
26,3
30,0
25,0
26,1
27,1
28,1
Modelo
M9
Caso
Referencia
Tope
Base
Crítico
Hipótesis
H5
H10
H15
H20
H5
H10
H15
H20
H5
H10
H15
H20
Espacio entre columnas
Primero
35,7
35,9
36,5
36,8
37,1
36,1
36,7
37,0
37,9
36,3
36,8
37,9
39,2
Central
5,0
5,8
6,6
7,4
8,1
6,5
7,1
7,6
8,3
7,3
8,4
9,7
10,9
Último
35,6
35,9
36,2
36,7
37,0
36,0
36,3
36,8
37,6
36,1
36,5
37,7
39,0
Modelo
M10
Caso
Referencia
Tope
Base
Crítico
Hipótesis
H5
H10
H15
H20
H5
H10
H15
H20
H5
H10
H15
H20
Espacio entre columnas
Primero
35,4
35,7
36,4
38,0
39,0
36,3
37,2
38,1
40,1
36,9
39,3
41,6
42,5
Central
2,7
3,3
5,0
8,9
10,1
3,3
5,9
9,0
10,3
4,0
6,6
9,9
12,0
Último
34,8
35,2
35,9
37,4
38,3
35,8
36,7
37,6
39,6
36,1
38,9
40,0
42,1
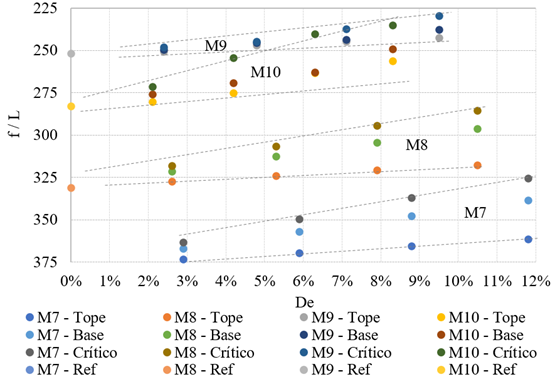
Figura 8.
Desplazamientos relativos para los diferentes modelos de losas.
Tabla 8. Análisis del balanceo de cargas para las losas (valores en %).
Modelo
M7
Caso
Referencia
Tope
Base
Crítico
Hipótesis
0,5
1,0
1,5
2,0
0,5
1,0
1,5
2,0
0,5
1,0
1,5
2,0
Espacio entre columnas
Primero
73
73
72
72
71
73
72
72
71
72
71
70
69
Central
74
72
71
69
68
72
71
69
68
71
68
64
61
Último
80
79
79
78
77
79
78
77
75
78
76
74
72
Modelo
M8
Caso
Referencia
Tope
Base
Crítico
Hipótesis
0,5
1,0
1,5
2,0
0,5
1,0
1,5
2,0
0,5
1,0
1,5
2,0
Espacio entre columnas
Primero
82
81
80
79
78
81
80
78
77
80
78
75
73
Central
92
89
87
84
82
89
87
84
82
87
82
77
72
Último
87
87
86
85
84
86
84
83
81
85
82
80
78
Modelo
M9
Caso
Referencia
Tope
Base
Crítico
Hipótesis
0,5
1,0
1,5
2,0
0,5
1,0
1,5
2,0
0,5
1,0
1,5
2,0
Espacio entre columnas
Primero
88
87
86
85
83
60
59
57
56
60
57
54
52
Central
94
92
90
88
85
61
60
58
57
60
56
53
50
Último
87
86
85
84
83
59
58
57
56
58
56
54
52
Modelo
M10
Caso
Referencia
Tope
Base
Crítico
Hipótesis
0,5
1,0
1,5
2,0
0,5
1,0
1,5
2,0
0,5
1,0
1,5
2,0
Espacio entre columnas
Primero
97
96
95
94
93
95
93
91
89
94
91
88
85
Central
93
92
90
88
86
92
90
88
86
90
86
83
79
Último
88
87
87
86
85
87
95
83
81
86
83
80
77
Tabla 9. Resultado armadura positiva de las losas
Modelo de análisis
Hipótesis e casos de cálculo
Referencia
H5 - Tope
H5 - Base
Espacio primero e último
Espacio central
Espacio primero e último
Espacio central
Espacio primero e último
Espacio central
Área de acero (cm2/m)
Área de acero (cm2/m)
Área de acero (cm2/m)
M7
2,54
2,11
2,54
2,11
2,64
2,22
M8
2,72
2,10
2,72
2,10
M9
3,26
2,40
3,26
2,40
M10
3,74
2,46
3,74
2,46
Tabla 10. Armadura negativa de las losas.
Modelo de análisis
Hipótesis y casos de cálculo
Referencia
H5 - Tope
H5 - Base
Área de acero (cm2/m)
M7
7,4
7,4
7,7
M8
10,5
10,5
M9
12,2
12,2
M10
15,6
15,6
