| Investigación aplicada | https://doi.org/10.21041/ra.v12i1.562. |
Vida útil à fadiga do concreto: Estudo experimental da influência das condições de carregamento e da resistência do material
Fatigue life of concrete: Experimental study on the influence of loading conditions and material strength
Vida de fatiga del hormigón: estudio experimental sobre la influencia de las condiciones de carga y la resistencia del material
E. F.
Felix1
*
![]() ,
R.
Carrazedo1
,
R.
Carrazedo1
![]() ,
E.
Possan2
,
E.
Possan2
![]()
1 University of São Paulo at São Carlos School of Engineering, Brasil..
2 Universidade Federal da Integração Latino-Americana (UNILA), Brasil.
*Contact author: emerson.felipe.felix@gmail.com
Recepção:
31
de
outubro
de
2021.
Aceitação:
07
de
dezembro
de
2021.
Publicação: 01 de janeiro de 2022.
| Citar como: Felix, E. F., Carrazedo, R., Possan, E. (2022), "Vida útil à fadiga do concreto: Estudo experimental da influência das condições de carregamento e da resistência do material", Revista ALCONPAT, 12 (1), pp. x-x, DOI: https://doi.org/10.21041/ra.v12i1.562 |
Resumo
O presente trabalho apresenta uma investigação experimental com objetivo de avaliar a influência da frequência de carregamento, intensidade da carga e resistência à compressão do material, no comportamento à fadiga do concreto. Ensaios foram realizados considerando três frequências de carregamento (0,125, 0,25 e 0,5 Hz), dois níveis de tensão máxima (50% e 70% da resistência à compressão) e concretos com três classes de resistência (30, 50 e 70 MPa). Os resultados encontrados apontam que à medida que a frequência de carregamento é aumentada, a vida útil à fadiga cresce exponencialmente. No entanto, observou-se que a vida útil à fadiga é menor em concretos de alta resistência e que a VUF apresentou uma relação inversa com a resistência à compressão.
Palavras chave:
concreto,
compressão cíclica,
fadiga,
fadiga de baixo ciclo,
vida útil à fadiga.
1. IntroduÇÃo
Estruturas de concreto, são geralmente projetadas diante da hipótese de que as cargas que atuarão ao longo de sua vida útil serão estáticas e que os elementos estruturais trabalham em regime elástico linear (ou com baixo nível de danificação). Entretanto, solicitações cíclicas como a ação do vento, as ondas de marés, os abalos sísmicos, os efeitos de temperatura e outras cargas flutuantes (como o tráfego de veículos em uma ponte), podem levar à falha da estrutura sob níveis de tensões abaixo dos estabelecidos em projeto, e isto ocorre devido ao fenômeno da fadiga (Lü et al., 2004; Saini e Singh, 2020).
A fadiga se refere a deterioração ou ruptura de um sólido quando submetido à repetidas cargas e descargas, e ocorre devido à degradação permanente e progressiva na microestrutura do material, para solicitações cíclicas de magnitude inferior à sua resistência (Saini e Singh, 2020). Assim, a fadiga é um fenômeno que deve ser considerando no projeto de elementos que trabalham sob ação de cargas cíclicas, a fim de que os danos permanentes que comprometem a integridade estrutural sejam minimizados.
De modo geral, o nível de tensão, que age no material, é de suma importância na análise e determinação da resistência à fadiga, ou vida útil (número de ciclos N, resistido antes da ruptura). O número N, pode ser descrito através da curva de Wöhler, ou curva SxN “Stress vs. Number”, que relaciona o nível de tensão aplicado ao número de ciclos que causam a ruptura no material. Para a maioria dos materiais, a curva de Wöhler mostra a existência de uma tendência na redução do número de ciclos à medida em que aumenta o nível de tensão (Dowling, 2012).
Atualmente, apenas os materiais dúcteis, como os aços e as ligas, apresentam ábacos e curvas de Wöhler bem definidas. Para o concreto e outros materiais frágeis e quase-frágeis, ainda não existem curvas definidas para todas as classes e tipos, uma vez que o desenvolvimento de pesquisas relacionadas à fadiga só ganhou destaque no decorrer das duas últimas décadas, ao passo em que os estudos correlatos às áreas de durabilidade, mecânica da fratura e mecânica do dano tiveram substancial avanço.
No que diz respeito ao desempenho do concreto quando submetido a cargas cíclicas, trabalhos vêm sendo desenvolvidos por estudos teóricos, experimentais e/ou numéricos, e divididos quanto ao tipo de fadiga analisada, fadiga por tração (Subramaniam e Shah, 2003; Chen, et al., 2017), tração-compressão (Lü et al., 2004), compressão (Xiao et al., 2013; Lantsoght et al., 2016; Jiang et al., 2017) e flexão (Kim et al., 2013; Arora e Singh, 2016; Kasu et al., 2019; Saiani e Sinsh, 2020). A maioria das pesquisas encontradas na literatura têm como objetivo a avaliação da fadiga à flexão, onde as tensões de tração são preponderantes.
No Brasil, por exemplo, as pesquisas são prioritariamente relacionadas à fadiga por flexão em vigas ou compressão e flexão em pavimentos de concreto, sendo a maioria de cunho numérico ou teórico-numérico (Baroni, 2010; Junges, 2017; Mascarenhas e Carvalho, 2019).
A principal dificuldade encontrada para o estudo experimental do comportamento do concreto à fadiga, no Brasil, remete-se à incipiência de equipamentos capazes de realizar ensaios cíclicos com alta velocidade de carregamento. Medeiros (2012), por exemplo, realizou parte de sua pesquisa no exterior, devido a indisponibilidade, na época, de máquinas e equipamentos de laboratório para ensaios de fadiga à compressão. O autor analisou experimentalmente o ganho de resistência à fadiga devido a incorporação de fibras na matriz cimentante do concreto, verificando ainda, a influência de distintas frequências de carregamento.
Diante do exposto, este trabalho tem como objetivo investigar o comportamento à fadiga do concreto, a fim de analisar a vida útil à fadiga (VUF) de concretos de baixa (30 MPa), e alta (50 e 70 MPa) resistência à compressão, submetidos à diferentes condições de carregamento. O estudo experimental foi desenvolvido considerando a compressão cíclica, onde os ensaios foram realizados pela combinação de três frequências de carregamento (0,125, 0,25 e 0,5 Hz) e dois níveis de tensão máxima (50% e 70% da resistência à compressão).
2. Fadiga no concreto
2.1 Degradação do material devido a cargas cíclicas
Em corpo sujeito a cargas cíclicas, nucleações em nível microscópico são originadas com um baixo número de repetições devido ao efeito da fadiga no material. A progressão das fissuras até a sua observação em nível macroscópico é lenta, se considerada a vida útil à fadiga do sólido, usualmente expressa pelo número de ciclos necessário para causar a falha do material (Nf).
A vida útil à fadiga (VUF) é geralmente classificada em dois estágios: um referente ao surgimento das nucleações no material e outro à propagação das fissuras. No período de iniciação também é observado o crescimento microestrutural de fissuras, porém em dimensões tão insignificantes que não são consideradas na representação ou quantificação do nível de danificação do material. Já o período de propagação, pode ser caracterizado pelo período que remete ao desenvolvimento das fissuras em nível mesoscópico. A Figura 1 apresenta as diferentes fases que configuram a vida útil à fadiga, considerando aspectos relacionados à fissuração dos materiais.
 |
||||
| Figura 1. Fases da VUF associadas à fissuração do concreto | ||||
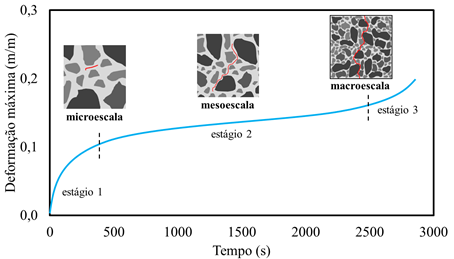
Do surgimento da primeira microfissura até a ruptura do material, o dano por fadiga no concreto pode ser caracterizado em três estágios (Figura 2): (i) origem da fissura, que é quando a microfissuras surgem devido à alta concentração de tensões em pontos de descontinuidades na estrutura cristalina ou, em regiões com descontinuidades pré-existentes no material; (ii) propagação da fissura, devido ao acúmulo de energia nas extremidades das fissuras existentes; e (iii) ruptura do material, que ocorre de maneira abrupta, devido à natureza quase-frágil do material.
 |
||||
| Figura 2. Avanço de fissuras no concreto em função da deformação máxima e do tempo de ensaio em corpos de prova submetidos à carga cíclica. | ||||
Para prever ou monitorar a vida útil de um elemento de concreto quando sujeito à fadiga, faz-se necessário conhecer o comportamento mecânico do material quando submetido à ciclos de carga e descarga. As propriedades do concreto referentes à fadiga são determinadas a partir de ensaios laboratoriais, onde os dados obtidos são geralmente apresentados por meio do gráfico de tensão ou de deformação específica em função do número de ciclos até a ruptura, curva S-N e ε-N, respectivamente.
Existem na literatura diversos modelos de previsão da vida útil do concreto quando submetido à fadiga, conforme apresentado nas Equações (1)-(3) (Wöhler, 1960; Raithby e Galloway, 1974; Tepfers e Kutti, 1979). Entretanto, boa parte dos modelos possuem como diretriz as curvas S-N ou ε-N, obtidas em campanhas experimentais, às quais só atendem a um pequeno número de casos, o que inviabiliza o seu emprego de forma generalizada.
 |
 |
 |
onde S max é a tensão máxima aplicada, f t,f é a resistência à tração na flexão estática do concreto, N é o número de ciclos para o colapso do material, d e e são parâmetros do material obtido por regressão dos dados, R é a razão entre a tensão mínima e máxima, f est é a resistência característica do concreto, f est é a resistência em análise (tração, compressão ou flexão) ou tração estática do concreto.
De acordo com Lee e Barr (2004), são muitos os motivos que inviabilizam o uso da curva de Wöhler (Equação (1)) de forma generalizada, sendo a principal, a determinação dos parâmetros por meio da regressão de dados, uma vez que existe uma dispersão considerável nos resultados de ensaios de fadiga no concreto, considerando amostras do mesmo lote, sob as mesmas condições de ensaio.
Ortega et al. (2018) relatam que a grande dispersão nos resultados é decorrente da sensibilidade da resistência à fadiga a uma variedade de parâmetros relacionados ao ensaio e ao material, que são quase impossíveis de serem controlados de maneira precisa, como as condições de moldagem, o alinhamento do corpo de prova no equipamento de ensaio, a imposição das tensões máximas e mínimas, a frequência de carregamento e o posicionamento dos extensômetros ou Strain Gauges.
2.2 Fatores intervenientes na vida útil à fadiga
O estudo da fadiga no concreto, teve suas primeiras publicações em meados da década de 1920, com o trabalho de Clemmer (1922), onde foi observado que o concreto possui um comportamento distinto ao do aço, quando submetido a carregamento cíclico, observando que este mecanismo de degradação estava correlacionado aos princípios da mecânica da fratura.
Ao longo dos últimos cem anos, após a publicação dos primeiros trabalhos, muitos estudos de fadiga no concreto foram desenvolvidos, sendo a maioria (até a década de 90) referentes à determinação de um modelo geral, que considerasse os distintos tipos de ensaios à fadiga: tração direta, tração na flexão, tração por compressão, compressão e tração-compressão alternada.
De acordo com Medeiros (2012), o modo de carregamento influencia o comportamento do concreto à fadiga, uma vez que são distintos os fatores que governam o mecanismo de ruptura do concreto na compressão, tração ou flexão. Ademais, sabe-se que outros parâmetros podem influenciar na resistência à fadiga e vida útil, como os materiais constituintes, condições de umidade, relação entre tensões mínima e máxima (R), frequência de carregamento, entre outras.
Raithby e Galloway (1974) analisaram a influência das condições de umidade na determinação do número de ciclos até a ruptura do concreto convencional. Os autores analisaram as condições do concreto saturado, concreto seco ao ar por uma semana (Equação (2)) e concreto seco em forno por uma semana. Os resultados encontrados foram coincidentes com os observados por Cornelissen e Lewis (1986), onde o concreto saturado apresenta vida útil inferior ao do concreto seco ao ar, mas praticamente a mesma que o concreto seco em forno.
Tepfers e Kutti (1979) propuseram modelos para a determinação da vida útil de concretos submetidos à fadiga por compressão, tração e flexão, verificando por meio de análises estatísticas, que a Equação (3) atende aos diferentes tipos de carregamento. Entretanto, Cornelissen (1984) apresentou um estudo demonstrando que o modo de carregamento tem influência no comportamento do concreto à fadiga, indicando que um único modelo não representaria adequadamente o fenômeno para os diferentes tipos de carregamentos. Ademais, Cornelissen (1984) e Zhang et al. (1996) verificaram que os ensaios alternados causam maior redução na resistência à fadiga do que aqueles puramente em tração na flexão.
No que se refere aos materiais constituintes, ainda não se chegou à um consenso quanto a influência da relação água/cimento (a/c) e do consumo de cimento, os estudos de Tepfers e Kutti (1979) e Zhang et al. (1997) mostram que estes parâmetros são indiferentes ao comportamento do concreto submetido à fadiga por tração ou flexão, afetando apenas a resistência estática do material.
Quanto ao tipo de agregado empregado, Sparks (1982) mostrou que existe uma forte correlação entre a taxa de deformação secundária e o número de ciclos até a ruptura do concreto, fazendo com que concretos produzidos com agregado leve tenham uma menor vida útil, quando comparados aos concretos com agregado convencional (agregados de origem basáltica ou granítica).
Por fim, sabe-se que frequência de carregamento (f) pode exercer grande influência no comportamento à fadiga do concreto, e mais, que ao se elevar a frequência, a vida útil à fadiga aumenta. Porém, a maioria dos trabalhos existentes na literatura, que corroboram com essa afirmação, foram desenvolvidos para altas frequências (f > 1,0) e para tensões máximas variando entre 75% e 95% da resistência estática (Zhang et al., 1996). Jansen (1996) observou que para tensão máxima menor que 75% da resistência estática do concreto, as frequências entre 1 e 15 Hz apresentam pequena influência na resistência à fadiga, e mais, que uma redução de 100 vezes na frequência resulta numa redução de 10 a 30 vezes no número de ciclos.
3. Campanha experimental
A metodologia utilizada neste trabalho é definida em cinco etapas, cujo objetivo centra-se na avaliação da vida útil à fadiga de corpos de prova cilíndricos submetidos à compressão cíclica.
 |
||||
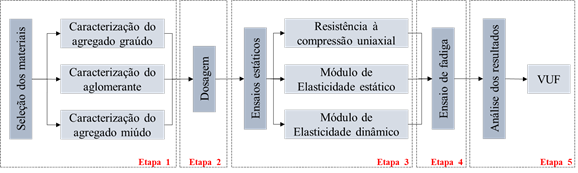
| Figura 3. Metodologia do trabalho. | ||||
As cinto atividades desenvolvidas no trabalho são apresentadas na Figura 3, e referem-se à: i) seleção e caracterização dos materiais; ii) dosagem e moldagem dos concretos; iii) ensaios para definição de propriedades mecânicas do material; iv) ensaio de fadiga à compressão; e (v) análise dos resultados obtidos. Cada uma destas atividades é descrita detalhadamente a seguir.
3.1 Seleção e caracterização dos materiais
Neste estudo, para a produção dos concretos, empregou-se como aglomerante o cimento Portland CP II Z 32, composto com pozolana e com 32 MPa de resistência à compressão. A massa específica (3,06 g/cm³) e a área superficial específica (3965,00 cm²/g) deste cimento foram determinadas de acordo com a NBR NM 23:2001 (ABNT, 2001) e com a NBR 16372:2015 (ABNT, 2015), respectivamente.
Areia quartzosa e brita 0 de origem basáltica foram empregadas como agregados miúdo e graúdo, respectivamente. Para a caracterização dos agregados (Tabela 1), foram realizados os ensaios de composição granulométrica, massa específica, massa unitária, absorção de água e módulo de finura.
Quanto à composição granulométrica do agregado miúdo, verificou-se que os dois lotes analisados se encaixam dentro dos limites granulométricos recomendados pela NBR 7211 (ABNT, 2009) para areia fina. Em relação aos agregados graúdos, os resultados comprovaram a dimensão máxima característica de 9,5 mm, correspondente a brita 0.
| Tabela 1. Caracterização física dos agregados. | ||||||||||||||
| Propriedades | Agregado miúdo | Agregado graúdo | Normas utilizadas | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Massa unitária (kg/m3) | 1390 | 1401 | NBR NM 45: 2006 | |||||||||||
| Massa especifica (kg/m3) | 2520 | 2590 | NBR NM 53: 2003 | |||||||||||
| Absorção (%) | 0.22 | 1.45 | NBR NM 53, 2003 | |||||||||||
| Módulo de finura | 1.46 | - | NBR NM 248 2003 | |||||||||||
Para os concretos de classe C50 e C70, foram necessários empregar aditivos superplastificantes, que são compostos de polímeros orgânicos, comumente empregados como redutores de água, que possibilitam a redução do fator água/cimento e para dispersar partículas de cimento, melhorando assim a fluidez dos traços.
Por fim, relata-se que em todas as concretagens foi utilizada água potável proveniente da rede de abastecimento local, sendo dispensável o controle de sua aceitação.
3.2 Dosagem e produção dos concretos
Para a definição do programa experimental, foram produzidos concretos considerando três diferentes composições, sendo uma para um concreto convencional de baixa resistência, com resistência característica à compressão igual a 30 MPa (C30) e dois para concretos de alta resistência, com 50 (C50) e 70 MPa (C70).
Para a dosagem, utilizou-se o método da ABCP (Rodrigues, 1984) com abatimento fixado em (120 ± 20) mm. Foram feitas dosagens iniciais para que o a composição dos materiais proporcionasse concretos com as resistências almejadas. Na Tabela 2 são apresentados os consumos de materiais para cada um dos traços produzidos.
Ao todo, foram produzidos 126 corpos de prova cilíndricos de 5 cm de diâmetro e 10 cm de altura, sendo 42 corpos de prova para cada um dos três lotes. Os concretos foram moldados em mesa vibratória e submetidos à cura com temperatura e umidade controladas até o instante de realização dos ensaios, aos 28 e 90 dias.
| Tabela 2. Consumo de materiais. | ||||||||||||||
| Material | Consumo de material em kg/m3 | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C30 | C50 | C70 | ||||||||||||
| Cimento (CP II Z 32) | 353.96 | 395.55 | 553.43 | |||||||||||
| Agregado miúdo | 800.44 | 1000.76 | 853.92 | |||||||||||
| Agregado graúdo | 1023.68 | 819.96 | 826.75 | |||||||||||
| Água | 184.19 | 166.37 | 168.92 | |||||||||||
| Aditivo | - | 2.38 | 4.41 | |||||||||||
| Relação água/cimento | 0.52 | 0.42 | 0.3 | |||||||||||
3.3 Ensaios com carregamentos estáticos
Para os ensaios de caracterização dos concretos com carregamento estático, foram utilizados dezoito corpos de prova, sendo seis empregados nos ensaios de resistência à compressão aos 7 dias, seis aos 28 dias, seis para análise da resistência e determinação do módulo de elasticidade estático e dinâmico aos 90 dias (período em que ocorreram os ensaios de compressão cíclica). Os ensaios foram conduzidos de acordo com as normas NBR 5739 (ABNT, 2007), NBR 8522 (ABNT, 2017) e ASTM E1876 (2015).
O módulo de elasticidade dinâmico foi considerado neste trabalho, por ser uma propriedade que representa o comportamento do concreto quando submetido a cargas dinâmicas. Os ensaios do módulo de elasticidade dinâmico foram realizados por meio da técnica de excitação por impulso (TEI), uma técnica não destrutiva, a qual permite que o corpo de prova seja empregado em outro ensaio. Este ensaio foi realizado com o propósito de determinar a variação do módulo de elasticidade e o dano correspondente, avaliado durante a realização do ensaio de fadiga.
O módulo de elasticidade dinâmico e seu respectivo módulo estático, obtido via formulação de Popovics (2008) (Equação (4)), foi mensurado em seis corpos de prova antes do início dos ensaios de resistência à compressão aos 90 dias.
 |
onde E c é o módulo de elasticidade estático (em Pa), ρ é a densidade do concreto (em kg/m³), E d é o módulo de elasticidade dinâmico (em Pa).
3.4 Ensaios de fadiga
Para a realização dos ensaios de fadiga, foram utilizados corpos de prova cilíndricos de 10 cm de altura e 5 cm de diâmetro, submetidos à compressão cíclica em uma máquina servo hidráulica Instron 8805 de capacidade máxima de ± 1500 kN. A escolha dos corpos de prova foi realizada buscando uma dimensão com que a velocidade máxima de carregamento usada nos ensaios fosse inferior à velocidade máxima suportada pela máquina (80 kN/s) e que ainda representasse adequadamente o comportamento do material. Como justificativa para a dimensão do corpo de prova, indica-se o estudo experimental realizado por Saini et. al. (2015), onde foi observado que para a fadiga à compressão, o diâmetro do corpo de prova possui influência superior à relação altura/diâmetro do corpo de prova e que um diâmetro igual ou superior a 5 cm é suficiente para avaliar e/ou ensaiar corpos de prova de concreto sob compressão cíclica. Saini et. al. (2015) relatam ainda, que deve ser utilizado um corpo de prova que apresente uma relação entre diâmetro do corpo de prova e diâmetro máximo do agregado superior à 5,00.
A máquina servo-hidráulica utilizada possui controle eletrônico que recebe sinais analógicos de até seis canais diferentes, seja carga, deslocamento ou leitura proveniente de um extensômetro qualquer. A Figura 4.a mostra uma visão geral da posição dos dois extensômetros do tipo roseta dupla (com direções variando em 90º) e dois LVDT, utilizados nos corpos de prova. Já na Figura 4.b é apresentado o esquema de carregamento cíclico empregado.
 |
||||
| Figura 4. Esquema (a) de instrumentação e (b) do carregamento cíclico. | ||||
Os ensaios de fadiga foram configurados por meio do controle de carga. Como apresentado na Figura 4.b, a definição das cargas máximas e mínimas foi realizada considerando duas configurações distintas, uma para a carga máxima de 50% da resistência à compressão (f c ) e outra para 70% de f c , considerando nos dois casos, uma carga mínima de 0 kN, o que configura relações entre tensões mínima e máxima (R) de 0,00 para os dois casos.
Foram analisados quatro corpos de prova para a determinação do número de ciclos médio, necessário para a ruptura por fadiga na compressão, para os dezoito casos estudados. Os dezoito casos se referem à combinação das três frequências de carregamento (0,125, 0,25 e 0,5 Hz), dos dois níveis de tensão máxima (50% e 70% de f c ) e das três classes de resistência à compressão (30, 50 e 70 MPa).
Para facilitar a leitura dos resultados, utilizou-se a nomenclatura C#S#F#, onde C# remete à classe de resistência do concreto (C30 para 30 MPa, C50 para 50 MPa ou C70 para 70 MPa), S# refere-se à tensão máxima adotada (S5 para 50% e S7 para 70%) e F# descreve a frequência do carregamento (F125 para 0,125 Hz, F25 para 0,25 Hz e F5 para 0,5 Hz).
4. Resultados
4.1 Caracterização
A caracterização das propriedades mecânicas dos concretos empregados no estudo experimental foi conduzida por meio de ensaios de resistência à compressão do concreto (f c ), módulo de elasticidade estático (E c ) e módulo de elasticidade dinâmico (E d ).
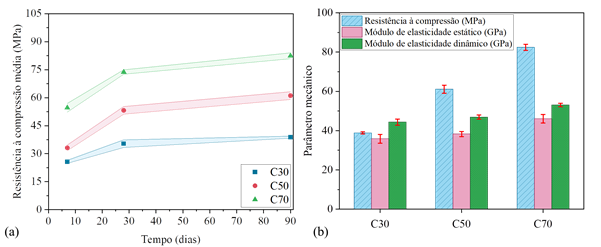
No que se refere à determinação da resistência à compressão dos concretos, ensaios de compressão estática foram conduzidos em seis corpos de prova para cada um dos traços. Os ensaios foram conduzidos aos 7, 28 e 90 dias, onde os concretos permaneceram em cura com temperatura e umidade controladas em 25°C e 75%, respectivamente. Na Figura 5.a são apresentadas as médias das resistências à compressão dos concretos, considerando os três instantes de tempo avaliados. As áreas sombreadas no gráfico representam a faixa de valores referentes à média ± o desvio padrão amostral.
Na Figura 5.b são apresentadas as médias dos resultados obtidos para todas as propriedades mecânicas avaliadas aos 90 dias. Os dados foram dispostos de modo a indicar a resistência à compressão, o módulo de elasticidade estático e o módulo de elasticidade dinâmico. Além disso, são apresentados os desvios padrão das propriedades avaliadas.
Os resultados de caracterização das propriedades mecânicas indicam que os concretos dosados apresentam resistência à compressão média, aos 28 dias, adequada à classe de resistência para o qual foram dosados, sendo as resistências médias de 35,35 MPa para o traço C30, 53,21 MPa para o traço C50 e 73,74 MPa para o traço C70.
 |
||||
| Figura 5. Médias e desvios da (a) resistência à compressão aos 7, 28 e 90 dias, e (b) da resistência à compressão, módulos de elasticidade estático e dinâmico aos 90 dias. | ||||
Quanto ao módulo de elasticidade estático, foi observado uma pequena variação do seu valor ao variar a resistência à compressão do material. Este resultado, corrobora com os estudos realizados por Vasconcellos (2018) e Graeff e Prudêncio Jr. (2016), onde foi verificado por meio de estudos experimentais que uma alteração significativa da resistência à compressão do concreto não configura, necessariamente, uma alteração significativa no valor do módulo de elasticidade, sendo importante avaliar outros parâmetros, à exemplo da relação água/cimento, teor de pasta cimentícia, e a proporção de agregados.
Com o objetivo de analisar os valores obtidos para os módulos estáticos e dinâmicos, a Equação (4) foi empregada para avaliar se o módulo de elasticidade estático, obtido experimentalmente, se aproximava do módulo de elasticidade estático estimado via módulo dinâmico. Dá aplicação da Equação (4), obteve-se para os concretos C30, C50 e C70, módulos estático iguais a 35,50, 39,27 e 45,65 GPa, respectivamente, enquanto os valores médios experimentais foram de 35,84, 38,29 e 46,05 GPa. A diferença percentual entre os valores obtidos na previsão e, os mensurados experimentalmente, foi de 0,94, 2,55 e 0,86%, para os concretos C30, C50 e C70, respectivamente. Este resultado denota o nível de acurácia da Equação (4) na previsão do módulo de elasticidade estático do concreto, considerando resultados obtidos via Técnica de Excitação por Impulso (TEI).
4.2 Vida útil à fadiga
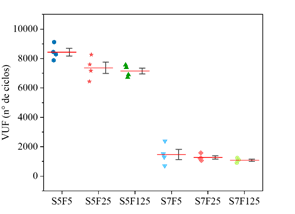
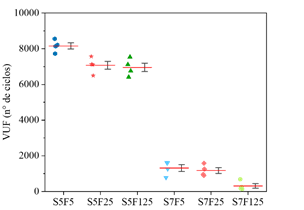
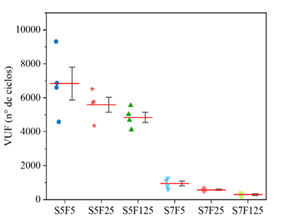
Diante dos diferentes cenários de carregamento considerados na campanha experimental, e considerando as propriedades mecânicas aferidas e dispostas nas Figuras 5.a e 5.b, nas Figuras 6-8 são apresentados os números de ciclos (VUF) que cada uma das quatro amostras ensaiadas, por compressão cíclica, resistiu antes de ocorrer a ruptura. Os resultados foram dispostos de modo a apresentar o número de ciclos necessários para causar a falha de cada um dos quatro corpos de prova (VUF) e a média dos valores obtidos em cada lote de amostragem (linha vermelha). Nos gráficos também são representados boxes contendo o primeiro e terceiro percentis.
A fim de avaliar a viabilidade dos modelos clássicos de previsão da vida útil à fadiga do concreto, as Equações (2) e (3) foram empregadas de modo a estimar a VUF dos concretos analisados neste trabalho. Os resultados obtidos foram confrontados com os observados experimentalmente.
Da aplicação da Equação (2), a VUF predita foi de 38 milhões de ciclos para concretos submetidos à tensão máxima de 50% da fc, e 200 mil ciclos para concretos submetidos à tensão máxima de 70% da fc, sendo estes valores muito superiores aos resultados dispostos nas Figuras 6-8. Já ao utilizar a Equação (3), a VUF predita foi inferior ao valor obtidos pela Equação (2), sendo calculada uma VUF de 19 milhões de ciclos para concretos submetidos à tensão máxima de 50% da fc, e 23 mil ciclos para concretos submetidos à tensão máxima de 70% da fc, resultado também muito superior aos obtidos experimentalmente. Cabe destacar que os resultados obtidos pelas formulações, não dependem da classe de resistência do material, e tão pouco, das condições de carregamento.
Assim, os resultados obtidos pelas Equações (2) e (3) denotam a importância do estudo do comportamento e vida útil à fadiga de concretos sujeitos a cargas cíclicas, a fim de entender melhor o comportamento do material e propor modelos que incorporem em suas formulações parâmetros atrelados às condições de carregamento e da rigidez do material.
 |
||||
| Figura 6. VUF dos concretos C30. | ||||
 |
||||
| Figura 7. VUF dos concretos C50. | ||||
 |
||||
| Figura 8. VUF dos concretos C70. | ||||
 |
||||
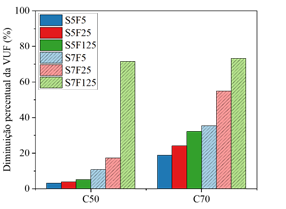
| Figura 9. Variação da vida útil à fadiga dos concretos C50 e C70 em relação ao C30 | ||||
Ao avaliar as Figura 6-8, é possível observar que mesmo para baixas frequências (f<1,0), o número de ciclos necessário para levar as amostras à ruptura, decresce à medida em que diminui a frequência de carregamento, comportamento observado também nos trabalhos de Zhang et al. (1996) e Medeiros (2012). Ademais, observa-se que este comportamento se apresenta independentemente do nível de tensão máxima aplicada (50% ou 70% de f c ), diferente do observado por Jansen (1996), onde o autor relata uma pequena ou quase inexistente influência da frequência na vida útil à fadiga de concretos com tensões máximas inferiores à 75% da resistência à compressão.
Corroborando com os resultados encontrados neste trabalho, o estudo experimental conduzido por Kim e Kim (1996), aponta que a vida útil à fadiga do concreto diminui na medida em que aumenta a tensão máxima aplicada e que essa característica possui maior evidência em concretos de alta resistência.
Com o propósito de avaliar a influência da resistência à compressão do concreto conjuntamente com a frequência do carregamento e o nível de tensão máxima na resistência à fadiga do material, na Figura 9 é apresentado um gráfico contendo a diminuição percentual da vida útil à fadiga (VUF) dos concretos de lote C50 e C70, em relação à VUF aferida nos concretos de lote C30.
Ao analisar os resultados dispostos nas Figuras 6,7,8,9, observa-se uma relação positiva entre a resistência à compressão do concreto e a vida útil à fadiga, sendo essa relação mais evidente quando da avaliação de concretos com resistência superior a 50 MPa (concretos de alta resistência). A influência da resistência à compressão na vida útil à fadiga foi investigada nos trabalhos de Al-Gadhib et al. (2000) e Kessler-Kramer et al. (2003), onde os autores indicam que a fragilidade que o material adquire ao ganhar resistência pode ser diretamente atrelada ao seu comportamento à fadiga, uma vez que a fadiga é definida pela degradação do material ao ser submetido a um carregamento cíclico.
Considerando os resultados dispostos na Figura 9 e sabendo que os concretos dos lotes C50 e C70 apresentam, respectivamente, resistências médias superiores a 57,37% e 112,33%, pôde-se inferir que a redução da VUF é maior para os concretos submetidos ao maior nível de tensão máxima aplicado (70% de f c ), independente da resistência do material. Ademais, observou-se que as reduções na VUF aumentam com a diminuição da frequência do carregamento adotado.
Dados os resultados apresentados nesta seção, infere-se um crescimento na vida útil à fadiga ao aumentar a frequência de carregamento, desde que mantido o mesmo nível de tensão aplicado no material. Ademais, observa-se que este comportamento é melhor visualizado quando da análise de concretos de alta resistência à compressão.
Uma possível justificativa encontrada por Chen et al. (2017) para explicar este fenômeno, refere-se ao fato de que na aplicação de carregamentos cíclicos, o concreto deixa de ter o seu comportamento definido por propriedades estáticas passando a ser mais bem representado por propriedades dinâmicas, que por sua vez são superiores às propriedades estáticas.
Por fim, comenta-se que durante os ensaios não foi observado um modo de ruptura característico para o concreto sob compressão cíclica. No entanto, assim como acontece nos ensaios de compressão estática, a ruptura do material se configurou de modo mais abrupta nos concretos de maior resistência à compressão. Ademais, pontua-se que a abrupta ruptura observada na falha dos concretos de alta resistência, foi maior nos ensaios cíclicos que nos ensaios de compressão estática, indicando que o nível de fragilidade do material é um parâmetro de influência no comportamento mecânico de concretos sujeitos a carregamentos cíclicos.
5. ConclusÕes
O comportamento mecânico do concreto submetido à compressão cíclica foi investigado experimentalmente neste trabalho por meio da avaliação da vida útil à fadiga, considerando concretos de três classes de resistência e sujeitos à diferentes condições de carregamento. Ao avaliar os resultados obtidos, pode-se indicar as seguintes considerações:
- A vida útil à fadiga é maior à medida que aumenta a frequência de carregamento aplicada, condição válida desde que mantido o nível de tensão máxima aplicado. Uma plausível justificativa levantada para este comportamento, se deve aos maiores valores das propriedades dinâmicas do material, comparados com os valores das propriedades físicas (Figura 6.b);
- O número de ciclos necessário para levar a amostra à ruptura é reduzido ao aumentar o nível de tensão máxima aplicado. Este comportamento foi verificado e associado ao aumento do nível de danificação do material, mensurado experimentalmente ao avaliar a redução do módulo de elasticidade tangente obtido do histórico dos carregamentos;
- Existe uma relação inversa entre a resistência à compressão do concreto e a vida útil à fadiga, sendo essa relação mais evidente quando da avaliação de concretos com resistência superior a 50 MPa (concretos de alta resistência);
- Ao considerar a variabilidade do número de ciclos necessário para gerar a ruptura do material (Figuras 6-8), observou-se que a dispersão dos dados em torno da média, decresce na medida em que diminui a frequência de carregamento, sendo este comportamento não dependente do nível de tensão máxima empregado. Este resultado pode indicar que o grau de confiabilidade de modelos de vida útil de componentes estruturais de concreto sujeitos à fadiga, deve ser inferido em função da frequência de carregamento ao qual as estruturas estão submetidas.
Por fim, comenta-se que este é o primeiro estudo experimental desenvolvido pelo grupo de pesquisa, e que no futuro, novos experimentos serão realizados a fim de estender as análises para outros níveis de tensão, frequência de carregamento e resistência à compressão do material. Como futuro trabalhos, pretende-se também propor curvas S-N para concretos submetidos à compressão cíclica, bem como formulações que auxiliem na análise o projeto à fadiga de elementos de concreto.
6. Agradecimentos
Os autores agradecem ao Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) (CNPq 141078/2018 e CNPq 310564/2018-2) e, à Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES código 001) pelo fomento fornecido à pesquisa.
REFERÊNCIAS
Associação Brasileira de Normas Técnicas (2001). NBR NM 23: Agregados - Determinação da composição granulométrica. Rio de Janeiro.
Associação Brasileira de Normas Técnicas (2003). NBR NM 248: Agregados - Determinação da composição granulométrica. Rio de Janeiro.
Associação Brasileira de Normas Técnicas (2006). NBR NM 45: Agregados - Determinação da massa unitária e do volume de vazios. Rio de Janeiro.
Associação Brasileira de Normas Técnicas (2007). NBR 5739: Concreto - Ensaios de compressão de corpos-de-prova cilíndricos. Rio de Janeiro.
Associação Brasileira de Normas Técnicas (2009). NBR 7211: Agregados para concreto - Especificações. Rio de Janeiro.
Associação Brasileira de Normas Técnicas (2008). NBR 8522: Concreto - Determinação do módulo estático de elasticidade à compressão. Rio de Janeiro.
Associação Brasileira de Normas Técnicas (2009). NBR NM 53: Agregado graúdo - Determinação da massa específica, massa específica aparente e absorção de água. Rio de Janeiro.
Associação Brasileira de Normas Técnicas (2015). NBR 16372: Cimento Portland e outros materiais em pó ― Determinação da finura pelo método de permeabilidade ao ar (método de Blaine). Rio de Janeiro.
Al-Gadhib, A. H., Baluch, M., Shaalan, A., Khan, A. (2000), Damage model for monotonic and fatigue response of high strength concrete. International Journal of Damage Mechanics, v. 9, n. 1, p. 57-78. https://doi.org/10.1177/105678950000900105
Arora, S., Singh, S. P. (2016), Analysis of flexural fatigue failure of concrete made with 100% Coarse Recycled Concrete Aggregates. Construction and Building Materials, v. 102, n. 1, p. 782-791. https://doi.org/10.1016/j.conbuildmat.2015.10.098
ASTM International (2015), ASTM E1876: Standard Test Method for Dynamic Young’s Modulus, Shear Modulus, and Poisson’s Ratio by Impulse Excitation of Vibration.
Baroni, H. J. M. (2010), “Simulação da vida útil de fadiga do concreto em vigas de tabuleiro de pontes em função do fluxo de veículos pesados”. Tese (Doutorado). Programa de Pós-Graduação em Engenharia Civil. Universidade Federal do Rio Grande do Sul. Porto Alegre.
Chen, X., BU, J., Fan, X., Lu, J., Xu, L. (2017), Effect of loading frequency and stress level on low cycle fatigue behavior of plain concrete in direct tension. Construction and Building Materials, v. 133, p. 367-375. https://doi.org/10.1016/j.conbuildmat.2016.12.085
Clemmer, H. F. (1922), Fatigue of concrete. Proceedings, American Society for Testing and Materials. v. 22, n. 2, p. 408-419.
Cornellissen, H. A. W. (1984), Fatigue failure of concrete in tension. Heron, v. 29, n. 4, p. 2-67.
Cornelissen, H. A. W., Lewis, M. (1986) “Fatigue experiments for the design of plain concrete pavements” in: Workshop on Theoretical Design of Concrete Pavements, CROW-PIARC-CEMBUREAU, Report 1, Holanda.
Dowling, N. E. (2012), “Mechanical behavior of materials: Engineering methods for deformation, fracture, and fatigue”. Practice Hall, 4th edition, United States.
Graeff, E.; Prudêncio Jr., L. R. (2016). Determinação do módulo de elasticidade dos concretos da central de Itajaí da Maxmohr. [S.l.]: Relatório técnico.
Jansen A. (1996), “Research to fatigue behaviour of topping on prefabricated concrete girders”. Thesis (Master). Delft University of Technology. Holanda.
Jiang, C., Xianglin, G., Huang, Q., Zhang, W. (2017), Deformation of concrete under high-cycle fatigue loads in uniaxial and eccentric compression. Construction and Building Materials, v. 141, p. 379-392. https://doi.org/10.1016/j.conbuildmat.2017.03.023
Junges, P. (2017), “Análise de fadiga em pontes curtas de concreto armado a partir de dados de sistemas B-WIM”. Tese (Doutorado). Centro Tecnológico: Programa de Pós-Graduação em Engenharia Civil. Universidade Federal de Santa Catarina. Florianópolis.
Kasu, S. R., Deb, S., Mitra, N., Muppireddy, A. R., Kusam, S. R. (2019), Influence of aggregate size on flexural fatigue response of concrete. Construction and Building Materials, v. 229, p. 1-9. https://doi.org/10.1016/j.conbuildmat.2019.116922
Kessler-Kramer, C., Mechtcherine, V., Mueller, H. S. (2003), “Failure of normal and high strength concrete under monotonic and cyclic tensile loading” in: Brittle Matrix Composites 7. Woodhead Publishing. p. 277-286. https://doi.org/10.1533/9780857093103.277
Kim, J. K., Kim, Y. Y. (1996), Experimental study of the fatigue behavior of high strength concrete. Cement and Concrete Research, v. 26, n. 10, p. 1513-1523.
Kim, J., Yi, C., Lee, S. J., Zi, G. (2013), Flexural fatigue behaviour of concrete under uniaxial and biaxial stress. Magazine of Concrete Research, v. 65, n. 12, p. 757-764. https://doi.org/10.1016/0008-8846(96)00151-2
Lantsoght, E. O. L., Van Der Veen, C., Boer, A. (2016), Proposal for the fatigue strength of concrete under cycles of compression. Construction and Building Materials, v. 107, p. 138-156. https://doi.org/10.1016/j.conbuildmat.2016.01.007
Lee, M. K., Barr, B. I. G. (2004), An overview of the fatigue behavior of plain and fiber reinforced concrete. Cement and Concrete Composites. v. 26, p. 299-305. https://doi.org/10.1016/S0958-9465(02)00139-7
Lü, P., Li, Q., Song, Y. (2004), Damage constitutive of concrete under uniaxial alternate tension-compression fatigue loading based on double bounding surfaces. International Journal of Solids and Structures, v. 41, p. 3151-3166. https://doi.org/10.1016/j.ijsolstr.2004.01.026
Mascarenhas, F. Jr. R., Carvalho, R. C. (2019), Vida útil à fadiga da armadura longitudinal de vigas de pontes de concreto armado frente ao tráfego real de veículos pesados. Revista AlCONPAT, v. 9, n. 3, p. 303-319. https://doi.org/10.21041/ra.v9i3.375
Medeiros, A. (2012), “Estudo do comportamento à fadiga em compressão do concreto com fibras”. Tese (Doutorado). Departamento de Engenharia Civil: Programa de Pós-graduação em Engenharia Civil. Pontifícia Universidade Católica do Rio de Janeiro. Rio de Janeiro.
Ortega, J. J., Ruiz, G., Yu, R. C., Afanador-García, N., Tarifa, M., Poveda, E., Zhang, X., Evangelista JR., F. (2018), Number of tests and corresponding error in concrete fatigue. International journal of fatigue, v. 116, p. 210-219. https://doi.org/10.1016/j.ijfatigue.2018.06.022
Popovics, J. S. (2008) “A study of static and dynamic modulus of elasticity of concrete”. University of Illinois, Urbana, IL. ACI-CRC Final Reports.
Raithby, K. D., Galloway, J. W. (1974), “Effects of moisture condition, age, and rate of loading on fatigue of plain concrete” in: ABELES Symposium: Fatigue of Concrete. ACI Publication, v. 41, p. 15-34.
Rodrigues, P. P. F. (1984), “Parâmetros de dosagem do cocreto.” São Paulo: ABCP, 1984.
Saini, B. S., Singh, S. P. (2020), Flexural fatigue life analysis of self-compacting concrete containing 100% coarse recycled concrete aggregates. Construction and Building Materials, v. 253, p. 1-13. https://doi.org/10.1016/j.conbuildmat.2020.119176
Sparks, P. R. (1982), Influence of rate of loading and material variability on the fatigue characteristics of concrete. ACI Journal, v. 75, n. 16, p. 331-342.
Subramaniam, K. V., Shah, S. P. (2003), Biaxial tension fatigue response of concrete. Cement and Concrete Composites, v. 25, n. 6, p. 617-623. https://doi.org/10.1016/S0958-9465(02)00075-6
Tepfers, R., Kutti, T. (1979), Fatigue strength of plain, ordinary and lightweight concrete. ACI Journal, v. 76, n. 29, p. 635-652.
Vasconcellos, A. T. D. (2018). “Estudo da variabilidade do módulo de elasticidade de concretos produzidos com diferentes tipos de agregados graúdos”. Dissertação (Mestrado). Departamento de Engenharia Civil: Programa de Pós-graduação em Engenharia Civil. Universidade Federal de Santa Catarina. Santa Catarina.
Xiao, J., Li, H., Yang, Z. (2013), Fatigue behavior of recycled aggregate concrete under compression and bending cyclic loadings. Construction and Building Materials, v. 38, p. 681-688. https://doi.org/10.1016/j.conbuildmat.2012.09.024
Zhang, B., Phillips, D. V., Wu, K. (1996), Effect of loading frequency and stress reversal of fatigue life of plain concrete. Magazine of Concrete Research, v. 48, n. 177, p. 361-375. https://doi.org/10.1680/macr.1996.48.177.361
Zhang, B., Phillips, D. V., Wu, K. (1997), Further research on fatigue properties of plain concrete. Magazine of Concrete Research, v. 49, n. 78, p. 241-252. https://doi.org/10.1680/macr.1997.49.180.241
