| Basic Research | https://doi.org/10.21041/ra.v12i1.562. |
Fatigue life of concrete: Experimental study on the influence of loading conditions and material strength
Vida útil à fadiga do concreto: Estudo experimental da influência das condições de carregamento e da resistência do material Vida de fatiga del hormigón: estudio experimental sobre la influencia de las condiciones de carga y la resistencia del material
E. F.
Felix1
*
![]() , R.Carrazedo1
, R.Carrazedo1
![]() , E. Possan2
, E. Possan2
![]() ,
,
1 University of São Paulo at São Carlos School of Engineering, Brasil.
2 Universidade Federal da Integração Latino-Americana (UNILA), Brasil.
*Contact author: emerson.felipe.felix@gmail.com
Reception: October 31, 2021.
Acceptance: December 07, 2021.
Publication: January 01, 2022
| Cite as: Felix, E. F., Carrazedo, R., Possan, E. (2022), "Fatigue life of concrete: Experimental study on the influence of loading conditions and material strength ", Revista ALCONPAT, 12 (1), pp. 1 – 15, DOI: https://doi.org/10.21041/ra.v12i1.562 |
Abstract
This work presents an experimental investigation aiming to evaluate the influence on the concrete fatigue behavior regarding the loading frequency, load intensity and the material’s compressive strength. Tests were carried out considering three loading frequencies (0.125, 0.25 and 0.5 Hz), two levels of maximum stress (50% and 70% of the compressive strength) and concretes made with three different compressive strength (30, 50 and 70 MPa). The results point out that as the loading frequency is increased, the fatigue life increases exponentially. However, it was observed that the fatigue life is shorter in high-strength concretes, i.e., the fatigue life presented an inverse relationship with the compressive strength.
Keywords:
concrete,
cyclic compression,
fatigue,
low cycle fatigue,
fatigue life,
hormigón,
compresión cíclica,
fatiga,
fatiga de bajo ciclo,
vida de fatiga,
concreto,
compressão cíclica,
fadiga,
fadiga de baixo ciclo,
vida útil à fadiga
Resumen
El presente trabajo presenta una investigación experimental con el objetivo de evaluar la influencia de la frecuencia de los esfuerzos, el nivel de tensión aplicada y la resistencia a la compresión del material sobre el comportamiento a fatiga del hormigón. Los ensayos se realizaron considerando tres frecuencias de carga (0,125, 0,25 y 0,5 Hz), dos niveles de tensión máxima (50% y 70% de la resistencia a la compresión) y hormigones con tres clases de resistencia a la compresión (30, 50 y 70 MPa). Los resultados encontrados indican que a medida que aumenta la frecuencia de carga, la vida en condiciones de fatiga aumenta exponencialmente. Sin embargo, se observó que la vida en condiciones de fatiga es menor en los hormigones de alta resistencia a la compresión, y presenta una relación inversa con la resistencia a la compresión del material.
1. Introduction
Concrete structures are usually designed under the assumption that loads are static throughout their useful life and that the structural elements behave as linearly elastic (or with low level of damage). However, cyclic loading sources such as wind, waves, tides, temperature effects and vehicle traffic can lead to structure failure even though the stresses levels are significantly below the established in project. This occurs due to fatigue failure (Lü et al., 2004; Saini and Singh, 2020).
Fatigue is the deterioration or failure of a solid due to repeated or cyclic loading and unloading. The failure occurs due to progressive degradation of the material’s microstructure developed by cyclical stresses of magnitude less than its strength (Saini and Singh, 2020). Thus, fatigue failures must be considered in the design of structural elements under cyclic loading so that damage is minimized.
In general, the magnitude of stresses is of leading importance in the analysis of endurance and service life (number of cycles N withstood before failure). The number N is described by a SN-Curve, or Wöhler curve, which is a plot that related the stress level due to cyclic loading versus the number of cycles to rupture. For most materials, the SN-Curve shows that the number of cycles reduces as the stress level is increased (Dowling, 2012).
Nowadays, only ductile materials have well-defined Wöhler curves and endurance limits. For brittle and quasi-brittle materials such as concrete, data is scatter for the several classes and types, since fatigue-related research has only increased on the last two decades, along with the substantial advances on fracture and damage mechanics and durability. Current research about the performance of concrete under cyclic loads is divided by the type of cyclic loading - tensile fatigue (Subramaniam and Shah, 2003; Chen, et al. al., 2017), tensile and compression (Lü et al., 2004), compression (Xiao et al., 2013; Lantsoght et al., 2016; Jiang et al., 2017), and flexure (Kim et al., 2013; Arora and Singh, 2016; Kasu et al., 2019; Saiani and Sinsh, 2020).
Most research aims to assess flexural fatigue strength and endurance limit, where tensile stresses are preponderant. In Brazil, for example, research is mainly devoted to flexural fatigue in beams and concrete pavements, mostly numerical and theoretical-numerical (Baroni, 2010; Junges, 2017; Mascarenhas and Carvalho, 2019). Experimental studies are incipient due to lack of equipment capable of performing cyclic loading at high speed. As an example, Medeiros (2012) carried out part of its experimental study abroad due to the unavailability of equipment for compressive fatigue tests. The author analyzed the fatigue strength gain due to the incorporation of fibers in the concrete as well as the influence of different loading frequencies.
Thus, this work evaluates the fatigue behavior of concrete, analyzing the fatigue life of concretes of low (30MPa) and high strength (50 and 70 MPa) under different loading conditions. Only cyclic compression loads with three loading frequencies (0.125, 0.25 and 0.5 Hz) and two levels of maximum stress (50% and 70% of the compressive strength) are considered in the experimental study.
2. Fatigue in concrete
2.1 Material degradation due to cyclic loads
In a body subject to cyclic loads, microscopic cracks develop with only a small number of cycles due to the effect of material fatigue. The evolution of their size is slow, and it is related to the fatigue life expressed by the number of cycles that lead to failure (N f ).
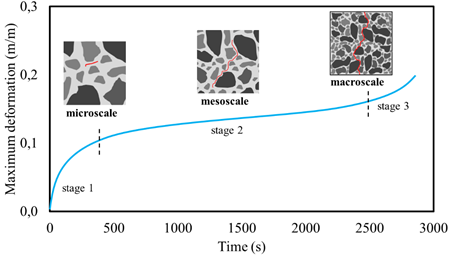
Fatigue life is usually classified into two stages: the nucleation of cracks, sometimes called initiation, and their propagation. In the nucleation period, the microstructural growth of cracks is observed but only with insignificant dimensions thus disregarded in the quantification of damage. On the other hand, the propagation period is characterized by the development of cracks at mesoscale. Figure 1 shows the phases that compose the fatigue life, considering aspects related to the material cracking.
 |
||||
| Figure 1. Fatigue life stages associated with concrete cracking. | ||||
In this sense, three stages characterize the fatigue damage of concrete, from the nucleation of the first micro-crack till rupture (as seen in Figure 2): (i) crack initiation, in which microcracks arise in discontinuities of the crystal structure due to stress concentration or in pre-existing material discontinuities; (ii) crack propagation, due to the energy accumulation at the ends of existing cracks; and (iii) failure, an abrupt rupture due to its quasi-brittle nature.
 |
||||
| Figure 2. Development of cracks in concrete due to cyclic loading as function of time and maximum strain. | ||||
To evaluate the useful fatigue life of a concrete element, one must know the mechanical behavior of the material when subject to loading and unloading cycles. The concrete properties associated to fatigue are accessed by laboratory tests, and data are usually expressed by stresses vs number of cycles to failure or specific deformation vs number of cycles to failure, S-N curve, and ε-N curve, respectively.
Several models have been proposed to predict the fatigue life of concrete, as presented in Equations (1) to (3) (Wöhler, 1960; Raithby and Galloway, 1974; Tepfers and Kutti, 1979).
 |
 |
 |
where S max is the maximum applied stress, f t,f is the static bending tensile strength, N is the number of cycles to failure, d and e are material parameters obtained by data regression, R is the ratio between the minimum and maximum stress, f ck is the concrete characteristic strength, f est is the strength under analysis (tensile, compression or bending) or static tension strength of the concrete.
Nevertheless, these models are usually based on S-N and ε-N curves obtained in experimental campaigns, which only attend to a small number of cases, making their general use unfeasible. According to Lee and Barr (2004), one of the reasons that make the general use of Wöhler curve unfeasible is that the parameters are obtained by data regression, and there is considerable dispersion in the fatigue tests on concrete, even under the same test conditions and sampling.
Ortega et al. (2018) report that the large dispersion in the results is associated to the sensitivity to parameters that are almost impossible to control, such as molding conditions, alignment of the specimen in the test equipment, correct imposition of maximum and minimum stresses, loading frequency and even the position of the strain gauges.
2.2 Factor influencing in fatigue life
The study of fatigue in concrete had its first publications in the mid-1920s with the work of Clemmer (1922), where it was observed that the degradation mechanism of concrete under cyclic loading was different from steel, and it was correlated to fracture mechanics instead. After that, until 1990s, many studies about endurance in concrete were developed, most of them focusing on the development of a general model considering the different types of fatigue tests: direct tension, tension due bending (flexural test), tension due compression (split tensile test), direct compression and cyclic tension-compression.
According to Medeiros (2012), the loading history influences the fatigue behavior of concrete, since the failure mechanism in compression, tension and bending are different. Furthermore, other parameters influence the endurance strength and service life, such as the constituent materials, moisture conditions, loading frequency, minimum and maximum applied stresses (R), among others.
Raithby and Galloway (1974) analyzed the influence of moisture conditions in the number of cycles to failure of conventional concrete. The authors analyzed the conditions of saturated concrete, air-dried concrete for one week (Equation (2)) and oven-dried concrete for one week and found that saturated concrete has lower service life than air-dried concrete, but practically the same as oven-dried concrete. Similar conclusions were found by Cornelissen and Lewis (1986).
Tepfers and Kutti (1979) proposed their own models to determine the useful fatigue life of concrete either by compression, tension or bending, verifying through statistical analysis that Equation (3) meets up for the different types of loading. However, Cornelissen (1984) proved that the loading mode has influence on the fatigue behavior of concrete, indicating that a single model would not adequately represent the phenomenon for different types of loading. Furthermore, Cornelissen (1984) and Zhang et al. (1996) found out that alternating stresses caused greater reduction in endurance strength.
With regard to the material constituents, there is still no consensus on the influence of the water/cement ratio (w/c) and cement consumption, although the studies by Tepfers and Kutti (1979) and Zhang et al. (1997) shown that these parameters are indifferent to the fatigue behavior of concrete subjected to either tension or bending, affecting only the static strength of the material.
As for the type of aggregate, Sparks (1982) showed that there is a strong correlation between the rate of deformation and the number of cycles until failures - concretes produced with light aggregate have shorter service life when compared to concretes produced with conventional aggregate (such as basaltic or granitic).
Finally, it is known that loading frequency (f) exerts great influence on the fatigue behavior of concrete, and moreover, that when the frequency is increased, the fatigue life is increased. However, most works with this same statement were also developed for high frequencies (f > 1,0) and maximum stresses varying between 75% and 95% of the compressive strength (Zhang et al., 1996). Jansen (1996) observed that frequencies between 1 and 15 Hz have little influence on endurance strength if the maximum stress is less than 75% of the concrete strength. Moreover, a reduction of 100 times in frequency reduces 10 to 30 times the number of cycles.
3. Experimental campaign
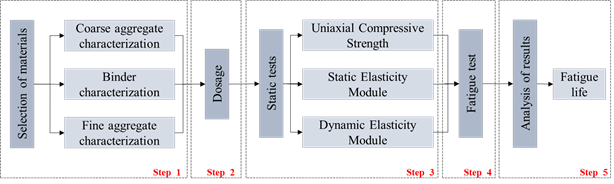
The campaign is divided in five stages (as seen in Figure 3), whose objective is to evaluate the fatigue life of cylindrical specimens submitted to cyclic compression. The first stage is the selection and characterization of material; second stage includes dosage of concrete mixture and casting; third stage is related to static tests to define the mechanical properties; in the fourth stage, compressive fatigue tests are made; finally, in the fifth stage there is the analysis of the results. These activities are described in detail in the sequence.
 |
||||
| Figure 3. Experimental campaign. | ||||
3.1 Selection and material characterization
In this study, Portland cement CP II Z 32 was used as binder, composed with pozzolan and with 32 MPa of compressive strength. The specific mass (3.06 g/cm³) and specific surface area (3965.00 cm²/g) were determined in accordance with NBR NM 23:2001 (ABNT, 2001) and NBR 16372:2015 (ABNT, 2015), respectively.
Quartz sand and gravel of basaltic origin were used as fine and coarse aggregates, respectively. Bulk density, relative density, water absorption and fineness modulus tests were carried out, as shown in Table 1. The granulometric composition of the fine aggregate shows that it is a fine sand, according to NBR 7211 (ABNT, 2009). As for the coarse aggregate, the nominal maximum aggregate size is 9.5 mm.
| Table 1. Physical properties of aggregates | ||||||||||||||
| Property | Fine aggregate | Coarse aggregate | Standard | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bulk density (kg/m3) | 1390 | 1401 | NBR NM 45: 2006 | |||||||||||
| Relative density (kg/m3) | 2520 | 2590 | NBR NM 53: 2003 | |||||||||||
| Absorption (%) | 0.22 | 1.45 | NBR NM 53, 2003 | |||||||||||
| Fineness modulus | 1.46 | - | NBR NM 248 2003 | |||||||||||
For concretes of classes C50 and C70, it was necessary a concrete superplasticizer, composed of organic polymers, commonly used to reduce water in the concrete mixes and increasing the fluidity. Also, tap water from local supply was used.
3.2 Dosage and concrete pouring
For the experimental program, three different compositions were adopted, one for conventional low-strength concrete with compressive strength of 30 MPa (C30), and two for high-strength concrete, with 50 (C50) and 70 MPa (C70).
Dosage was made by ABCP method (Rodrigues, 1984) with slump fixed at 120 ± 20 mm. Initial dosage attempts were also made to obtain concretes with the desired strengths. Table 2 shows the material consumption for each dosage.
| Table 2. Material consumption. | ||||||||||||||
| Material | Material consumption in kg/m3 | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C30 | C50 | C70 | ||||||||||||
| Cement (CP II Z 32) | 353.96 | 395.55 | 553.43 | |||||||||||
| Fine aggregate | 800.44 | 1000.76 | 853.92 | |||||||||||
| Coarse aggregate | 1023.68 | 819.96 | 826.75 | |||||||||||
| Water | 184.19 | 166.37 | 168.92 | |||||||||||
| Superplasticizer | - | 2.38 | 4.41 | |||||||||||
| Water/cement ratio | 0.52 | 0.42 | 0.3 | |||||||||||
126 cylindrical specimens with 5 cm diameter and 10 cm in height were produced, 42 specimens for each composition. The specimens were casted on a vibrating plate and cured afterwards at controlled temperature and humidity at 25°C and 75%, until testing, at 28 and 90 days.
3.3 Static tests
Eighteen specimens were used for concrete characterization for compressive strength with static loading - six specimens at 7 days after casting, six at 28 days, and six at 90 days. In this last group, static and dynamic modulus of elasticity were also evaluated (period in which cyclic compression tests also took place). These tests were conducted in accordance with standards NBR 5739 (ABNT, 2007), NBR 8522 (ABNT, 2017) and ASTM E1876 (2015).
Notice that it was considered in this work the dynamic modulus of elasticity, since it represents the behavior of concrete under dynamic loads. The modulus was stablished by the impulse excitation technique (IET) is a non-destructive technique, allowing to use the specimen in subsequent tests. The variation in the dynamic modulus of elasticity as the fatigue test was also measured, as an indirect measure of damage. Besides, the static modulus of elasticity was obtained from the dynamic modulus of elasticity using Equation (4) (Popovics, 2008)
 |
where E c is the static modulus of elasticity (in Pa), ρ is density (in kg/m³), and E d is the dynamic modulus of elasticity (in Pa).
3.4 Fatigue tests
The cylindrical specimens were subject to cyclic compression in an Instron 8805 servo-hydraulic testing system with loading capacity of ± 1500 kN. Notice that the size and compressive strength of the specimens were stablished by the maximum loading speed (80 kN/s) of the testing system. We also followed the experimental study carried out by Saini et al. (2015), in which it was observed that, for compressive fatigue tests, the diameter of the specimen has greater influence than the height / diameter ratio, and that the diameter of the specimen should be equal or greater than 5 cm. Saini et al. (2015) also report that the ratio between specimen diameter and maximum aggregate size should be greater than 5.0.
The servo-hydraulic system has an electronic control that receives analog signals from up to six different channels - load, displacement, or strain gauge. Figure 4a shows the adopted design for two rosette strain gauge and two LVDT, used in the specimens. Figure 4b shows the scheme used for the load controlled cyclic loading. Two configurations were defined for maximum load - 50% and 70% of the compressive strength (f c ), and the minimum load was always 0 kN, thus the ratio between the minimum and maximum stress R is 0.00 for both cases.
 |
||||
| Figure 4. Arrangement (a) of instrumentation and (b) of cyclic loading. | ||||
Since three speeds of loading were adopted (0.125, 0.25 and 0.5 Hz) along with two maximum compressive strength (50% and 70% of f c ) and three compressive strength classes (30, 50 and 70 MPa), eighteen different combinations were created. In each combination, four specimens were analyzed to stablish the average number of cycles for failure. The following code was adopted: C#S#F#, where C# refers to the compressive strength class (C30 for 30 MPa, as example), S# refers to the maximum compressive strength (S7 for 70%, for instance), and F# describes the speed of loading (F125 for 0.125 Hz, F25 for 0.25 Hz and F5 for 0.5 Hz).
4. Results
4.1 Material characterization
The characterization of the mechanical properties of the concretes used in the experimental study was conducted through tests of concrete compressive strength (f c ), static modulus of elasticity (E c ) and dynamic modulus of elasticity (E d ).
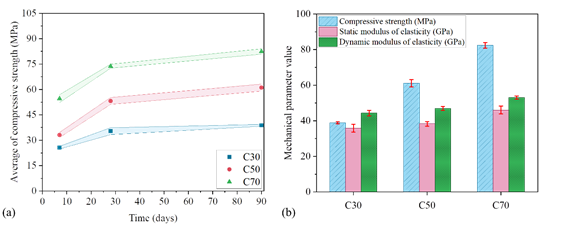
Static compression tests were carried out on six specimens for each mix at 7, 28 and 90 days. Specimens were kept curing with controlled temperature and humidity 25°C and 75%. Figure 5a shows the obtained average for the compressive strength. Shaded areas represent mean plus standard deviation. On the other hand, Figure 5b shows averages for the evaluated mechanical properties tested at 90 days. Standard deviation is also indicated.
Results show that, at 28 days, the obtained compressive strengths are suitable for the class they were poured, with an average strength of 35.35 MPa for C30, 53.21 MPa for C50 and 73.74 MPa for C70.
An expected variation on the static modulus of elasticity was observed, as seen in Vasconcellos (2018) and Graeff and Prudencio Jr. (2016). References shows that a significant variation in the compressive strength of concrete does not necessarily mean a significant variation in the value of the modulus of elasticity, and other parameters should be evaluated, such as water/cement ratio, paste content, and aggregate/cement ratio.
As mentioned before, Equation (4) assess the static modulus of elasticity from the dynamic modulus of elasticity obtained by using the Impulse Excitation Technique. From equation (4), the static modulus for concretes C30, C50 and C70 are 35.50, 39.27 and 45.65 GPa, respectively. As comparison, the mean experimental values for the static modulus were 35.84, 38.29 and 46.05 GPa. The percentage difference was 0.94, 2.55 and 0.86% for concretes C30, C50 and C70, respectively, showing that Equation (4) is suitable to predict the static modulus of elasticity based on the dynamic modulus.
 |
||||
| Figure 5. Mean and deviations of (a) compressive strength at 7, 28 and 90 days, and (b) compressive strength, static and dynamic modulus of elasticity at 90 days. | ||||
4.2 Fatigue life
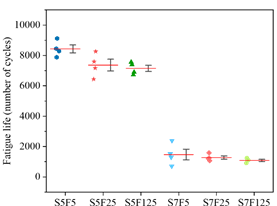
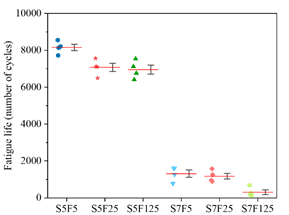
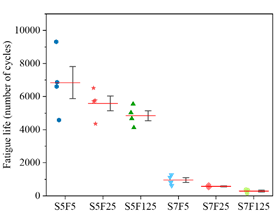
Figures 6, 7, 8 show the number of cycles before failure that each of the four samples endure, considering the different loading scenarios and maximum compressive strength attained. They also show the average of these results (red line), and boxes representing the first and third percentiles. Besides, experimental results are also compared to the estimations obtained in Equations (2) and (3).
Equation (2) predicted a fatigue life of 38 million cycles for concrete subject to a maximum stress of 50% f c and 200 thousand cycles for concrete subject to 70% f c , way higher than experimental results (see Figures 6, 7, 8). Equation (3), on the other hand, predicted a fatigue life of 19 million cycles for concretes subject to 50% f c and 23 thousand cycles for concrete subject to 70% f c , also higher than the experimental results. Nevertheless, notice that these equations do not depend on neither the strength class of the concrete nor the loading conditions. Thus, models should incorporate parameters associated with the loading pattern and the material stiffness.
From Figures 6, 7, 8, one may notice that the number of cycles to rupture decreases as the loading frequency decreases, as also observed by Zhang et al. (1996) and Medeiros (2012). Furthermore, this behavior is present regardless the maximum applied stress (50% or 70% of f c ), different from Jansen (1996), who states that there is almost no influence of the loading frequency in the fatigue life if maximum stresses are below 75% of the compressive strength. Nevertheless, the results found in this work follows Kim and Kim (1996), where authors point out that the fatigue life decreases as the maximum applied stress increases, especially in high-strength concrete.
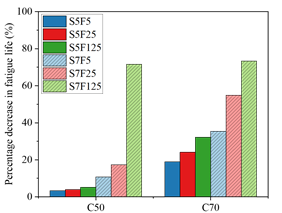
Figure 9 shows the decrease in fatigue life for concretes C50 and C70 when compared to C30, when the same loading frequency and maximum stress is applied. Thus, there is positive relationship between the compressive strength of concrete and its fatigue life, especially for high-strength concretes (C50 and C70). The influence of compressive strength on fatigue life was investigated by Al-Gadhib et al. (2000) and by Kessler-Kramer et al. (2003), where authors indicate that concrete is more prone to damage as strength is increased, and this can be linked to its fatigue behavior.
 |
||||
| Figure 6. Fatigue life for C30. | ||||
 |
||||
| Figure 7. Fatigue life for C50. | ||||
 |
||||
| Figure 8. Fatigue life for C70. | ||||
 |
||||
| Figure 9. Variation of fatigue life of concrete C50 and C70 compared to C30. | ||||
Considering the results shown in Figure 9, it can be inferred that the reduction in fatigue life is greater for concretes submitted to higher maximum applied stresses (70% f c ), regardless of material strength. Furthermore, it was observed that the fatigue life is reduced as loading frequency is reduced. Thus, an increase in fatigue life is expected when loading frequency is increased, as long as the stress level is kept the same. Besides, this behavior is even noticeable in high strength concretes.
Chen et al. (2017) brings up an explanation - the cyclic loads are associated to the dynamic properties of concrete, and the dynamic properties of concrete are often superior to its static counterpart.
Finally, the usual characteristic failure mode due to compressive loads was not observed for concrete under cyclic compression. However, rupture was still more abrupt in concretes with higher compressive strength. Furthermore, the rupture abruptness was even more pronounced in cyclic tests than in static compression tests, indicating that the material brittleness should be considered as an influencing parameter in the mechanical behavior of concrete under cyclic loads.
5. Conclusions
The mechanical behavior of concrete subjected to cyclic compression was experimentally investigated in this work. Concretes of three compressive strength classes were submitted to different loading conditions and the fatigue life was evaluated. The following conclusions were obtained:
- The fatigue life is increased as the loading frequency is increased if the maximum stress is maintained. A plausible justification is that the dynamic property of the material is higher than the static counterpart (see Figure 6b).
- The number of cycles until rupture is reduced as the maximum stress is increased. This is associated to the inner damage, here measured by the reduction of the modulus of elasticity using a non-destructive impulse excitation technique.
- There is an inverse relationship between the compressive strength and the fatigue life, which is even more pronounced in high strength concretes.
- Dispersion of the number of cycles before failure is decreased as the loading frequency decreases, no matter the applied maximum stress. This indicates that the loading frequency should be considered in fatigue life models.
Finally, the discussion here shall be extended to other levels of maximum stress, loading frequencies and compressive strengths. It is our aim to propose SN curves for concretes subjected to cyclic compression, as well as formulations to design concrete elements under fatigue.
6. Acknowledgment
The research supported by the Brazilian National Council for Scientific and Technological Development (CNPq 141078/2018, 310564/2018-2 and 428762/2018-2) is gratefully acknowledged. This study was also financed in part by the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior - Brasil (CAPES) - Finance Code 001
References
Associação Brasileira de Normas Técnicas (2001). NBR NM 23: Agregados - Determinação da composição granulométrica. Rio de Janeiro.
Associação Brasileira de Normas Técnicas (2003). NBR NM 248: Agregados - Determinação da composição granulométrica. Rio de Janeiro.
Associação Brasileira de Normas Técnicas (2006). NBR NM 45: Agregados - Determinação da massa unitária e do volume de vazios. Rio de Janeiro.
Associação Brasileira de Normas Técnicas (2007). NBR 5739: Concreto - Ensaios de compressão de corpos-de-prova cilíndricos. Rio de Janeiro.
Associação Brasileira de Normas Técnicas (2009). NBR 7211: Agregados para concreto - Especificações. Rio de Janeiro.
Associação Brasileira de Normas Técnicas (2008). NBR 8522: Concreto - Determinação do módulo estático de elasticidade à compressão. Rio de Janeiro.
Associação Brasileira de Normas Técnicas (2009). NBR NM 53: Agregado graúdo - Determinação da massa específica, massa específica aparente e absorção de água. Rio de Janeiro.
Associação Brasileira de Normas Técnicas (2015). NBR 16372: Cimento Portland e outros materiais em pó ― Determinação da finura pelo método de permeabilidade ao ar (método de Blaine). Rio de Janeiro.
Al-Gadhib, A. H., Baluch, M., Shaalan, A., Khan, A. (2000), Damage model for monotonic and fatigue response of high strength concrete. International Journal of Damage Mechanics, v. 9, n. 1, p. 57-78. https://doi.org/10.1177/105678950000900105
Arora, S., Singh, S. P. (2016), Analysis of flexural fatigue failure of concrete made with 100% Coarse Recycled Concrete Aggregates. Construction and Building Materials, v. 102, n. 1, p. 782-791. https://doi.org/10.1016/j.conbuildmat.2015.10.098
ASTM International (2015), ASTM E1876: Standard Test Method for Dynamic Young’s Modulus, Shear Modulus, and Poisson’s Ratio by Impulse Excitation of Vibration.
Baroni, H. J. M. (2010), “Simulação da vida útil de fadiga do concreto em vigas de tabuleiro de pontes em função do fluxo de veículos pesados”. Tese (Doutorado). Programa de Pós-Graduação em Engenharia Civil. Universidade Federal do Rio Grande do Sul. Porto Alegre.
Chen, X., BU, J., Fan, X., Lu, J., Xu, L. (2017), Effect of loading frequency and stress level on low cycle fatigue behavior of plain concrete in direct tension. Construction and Building Materials, v. 133, p. 367-375. https://doi.org/10.1016/j.conbuildmat.2016.12.085
Clemmer, H. F. (1922), Fatigue of concrete. Proceedings, American Society for Testing and Materials. v. 22, n. 2, p. 408-419.
Cornellissen, H. A. W. (1984), Fatigue failure of concrete in tension. Heron, v. 29, n. 4, p. 2-67.
Cornelissen, H. A. W., Lewis, M. (1986) “Fatigue experiments for the design of plain concrete pavements” in: Workshop on Theoretical Design of Concrete Pavements, CROW-PIARC-CEMBUREAU, Report 1, Holanda.
Dowling, N. E. (2012), “Mechanical behavior of materials: Engineering methods for deformation, fracture, and fatigue”. Practice Hall, 4th edition, United States.
Graeff, E.; Prudêncio Jr., L. R. (2016). Determinação do módulo de elasticidade dos concretos da central de Itajaí da Maxmohr. [S.l.]: Relatório técnico.
Jansen A. (1996), “Research to fatigue behaviour of topping on prefabricated concrete girders”. Thesis (Master). Delft University of Technology. Holanda.
Jiang, C., Xianglin, G., Huang, Q., Zhang, W. (2017), Deformation of concrete under high-cycle fatigue loads in uniaxial and eccentric compression. Construction and Building Materials, v. 141, p. 379-392. https://doi.org/10.1016/j.conbuildmat.2017.03.023
Junges, P. (2017), “Análise de fadiga em pontes curtas de concreto armado a partir de dados de sistemas B-WIM”. Tese (Doutorado). Centro Tecnológico: Programa de Pós-Graduação em Engenharia Civil. Universidade Federal de Santa Catarina. Florianópolis.
Kasu, S. R., Deb, S., Mitra, N., Muppireddy, A. R., Kusam, S. R. (2019), Influence of aggregate size on flexural fatigue response of concrete. Construction and Building Materials, v. 229, p. 1-9. https://doi.org/10.1016/j.conbuildmat.2019.116922
Kessler-Kramer, C., Mechtcherine, V., Mueller, H. S. (2003), “Failure of normal and high strength concrete under monotonic and cyclic tensile loading” in: Brittle Matrix Composites 7. Woodhead Publishing. p. 277-286. https://doi.org/10.1533/9780857093103.277
Kim, J. K., Kim, Y. Y. (1996), Experimental study of the fatigue behavior of high strength concrete. Cement and Concrete Research, v. 26, n. 10, p. 1513-1523.
Kim, J., Yi, C., Lee, S. J., Zi, G. (2013), Flexural fatigue behaviour of concrete under uniaxial and biaxial stress. Magazine of Concrete Research, v. 65, n. 12, p. 757-764. https://doi.org/10.1016/0008-8846(96)00151-2
Lantsoght, E. O. L., Van Der Veen, C., Boer, A. (2016), Proposal for the fatigue strength of concrete under cycles of compression. Construction and Building Materials, v. 107, p. 138-156. https://doi.org/10.1016/j.conbuildmat.2016.01.007
Lee, M. K., Barr, B. I. G. (2004), An overview of the fatigue behavior of plain and fiber reinforced concrete. Cement and Concrete Composites. v. 26, p. 299-305. https://doi.org/10.1016/S0958-9465(02)00139-7
Lü, P., Li, Q., Song, Y. (2004), Damage constitutive of concrete under uniaxial alternate tension-compression fatigue loading based on double bounding surfaces. International Journal of Solids and Structures, v. 41, p. 3151-3166. https://doi.org/10.1016/j.ijsolstr.2004.01.026
Mascarenhas, F. Jr. R., Carvalho, R. C. (2019), Vida útil à fadiga da armadura longitudinal de vigas de pontes de concreto armado frente ao tráfego real de veículos pesados. Revista AlCONPAT, v. 9, n. 3, p. 303-319. https://doi.org/10.21041/ra.v9i3.375
Medeiros, A. (2012), “Estudo do comportamento à fadiga em compressão do concreto com fibras”. Tese (Doutorado). Departamento de Engenharia Civil: Programa de Pós-graduação em Engenharia Civil. Pontifícia Universidade Católica do Rio de Janeiro. Rio de Janeiro.
Ortega, J. J., Ruiz, G., Yu, R. C., Afanador-García, N., Tarifa, M., Poveda, E., Zhang, X., Evangelista JR., F. (2018), Number of tests and corresponding error in concrete fatigue. International journal of fatigue, v. 116, p. 210-219. https://doi.org/10.1016/j.ijfatigue.2018.06.022
Popovics, J. S. (2008) “A study of static and dynamic modulus of elasticity of concrete”. University of Illinois, Urbana, IL. ACI-CRC Final Reports.
Raithby, K. D., Galloway, J. W. (1974), “Effects of moisture condition, age, and rate of loading on fatigue of plain concrete” in: ABELES Symposium: Fatigue of Concrete. ACI Publication, v. 41, p. 15-34.
Rodrigues, P. P. F. (1984), “Parâmetros de dosagem do cocreto.” São Paulo: ABCP, 1984.
Saini, B. S., Singh, S. P. (2020), Flexural fatigue life analysis of self-compacting concrete containing 100% coarse recycled concrete aggregates. Construction and Building Materials, v. 253, p. 1-13. https://doi.org/10.1016/j.conbuildmat.2020.119176
Sparks, P. R. (1982), Influence of rate of loading and material variability on the fatigue characteristics of concrete. ACI Journal, v. 75, n. 16, p. 331-342.
Subramaniam, K. V., Shah, S. P. (2003), Biaxial tension fatigue response of concrete. Cement and Concrete Composites, v. 25, n. 6, p. 617-623. https://doi.org/10.1016/S0958-9465(02)00075-6
Tepfers, R., Kutti, T. (1979), Fatigue strength of plain, ordinary and lightweight concrete. ACI Journal, v. 76, n. 29, p. 635-652.
Vasconcellos, A. T. D. (2018). “Estudo da variabilidade do módulo de elasticidade de concretos produzidos com diferentes tipos de agregados graúdos”. Dissertação (Mestrado). Departamento de Engenharia Civil: Programa de Pós-graduação em Engenharia Civil. Universidade Federal de Santa Catarina. Santa Catarina.
Xiao, J., Li, H., Yang, Z. (2013), Fatigue behavior of recycled aggregate concrete under compression and bending cyclic loadings. Construction and Building Materials, v. 38, p. 681-688. https://doi.org/10.1016/j.conbuildmat.2012.09.024
Zhang, B., Phillips, D. V., Wu, K. (1996), Effect of loading frequency and stress reversal of fatigue life of plain concrete. Magazine of Concrete Research, v. 48, n. 177, p. 361-375. https://doi.org/10.1680/macr.1996.48.177.361
Zhang, B., Phillips, D. V., Wu, K. (1997), Further research on fatigue properties of plain concrete. Magazine of Concrete Research, v. 49, n. 78, p. 241-252. https://doi.org/10.1680/macr.1997.49.180.241
