| Investigación aplicada | https://doi.org/10.21041/ra.v12i1.562. |
Vida de fatiga del hormigón: estudio experimental sobre la influencia de las condiciones de carga y la resistencia del material
Fatigue life of concrete: Experimental study on the influence of loading conditions and material strength
Vida útil à fadiga do concreto: Estudo experimental da influência das condições de carregamento e da resistência do material
E. F.
Felix1
*
![]() ,
R.
Carrazedo1
,
R.
Carrazedo1
![]() ,
E.
Possan2
,
E.
Possan2
![]()
1 University of São Paulo at São Carlos School of Engineering, Brasil.
2 Universidade Federal da Integração Latino-Americana (UNILA), Brasil.
*Contact author: emerson.felipe.felix@gmail.com
Recepción:
31
de
octubre
de
2021.
Aceptación:
07
de
diciembre
de
2021.
Publicación: 01 de enero de 2022.
| Citar como: Felix, E. F., Carrazedo, R., Possan, E. (2022), "Vida útil a la fatiga del hormigón: estudio experimental de la influencia de las condiciones de carga y resistencia del material", Revista ALCONPAT, 12 (1), pp. 1 – 15, DOI: https://doi.org/10.21041/ra.v12i1.562 |
Resumen
El presente trabajo presenta una investigación experimental con el objetivo de evaluar la influencia de la frecuencia de los esfuerzos, el nivel de tensión aplicada y la resistencia a la compresión del material sobre el comportamiento a fatiga del hormigón. Los ensayos se realizaron considerando tres frecuencias de carga (0,125, 0,25 y 0,5 Hz), dos niveles de tensión máxima (50% y 70% de la resistencia a la compresión) y hormigones con tres clases de resistencia a la compresión (30, 50 y 70 MPa). Los resultados encontrados indican que a medida que aumenta la frecuencia de carga, la vida en condiciones de fatiga aumenta exponencialmente. Sin embargo, se observó que la vida en condiciones de fatiga es menor en los hormigones de alta resistencia a la compresión, y presenta una relación inversa con la resistencia a la compresión del material.
Palabras claves:
hormigón,
compresión cíclica,
fatiga,
fatiga de bajo ciclo,
vida de fatiga.
1. IntroducciÓn
Las estructuras de hormigón/concreto suelen ser proyectadas bajo las hipótesis de que las cargas que actuarán a lo largo de su vida útil serán estáticas y que los elementos estructurales trabajan en régimen elástico lineal (o con un bajo nivel de deterioro). Sin embargo, las solicitaciones cíclicas, como la acción del viento, las mareas, los temblores sísmicos, los efectos de la temperatura y otras cargas fluctuantes (como el tráfico de vehículos en un puente), pueden provocar una avería en la estructura bajo niveles de tensión inferiores a los establecidos en el proyecto, y eso ocurre a causa del fenómeno de la fatiga (Lü et al., 2004; Saini y Singh, 2020).
La fatiga se refiere al deterioro o ruptura de un sólido cuando se somete a cargas y descargas repetidas, y se produce debido a la degradación permanente y progresiva en la microestructura del material para tensiones cíclicas de magnitud inferior a su resistencia (Saini y Singh, 2020). Por ello, la fatiga es un fenómeno que debe ser considerado en el proyecto de elementos que trabajan bajo la acción de cargas cíclicas, de manera que se minimicen los daños permanentes que comprometen la integridad estructural.
En general, el nivel de tensión, que actúa sobre el material, es de suma importancia en el análisis y definición de la resistencia a la fatiga, o vida útil (número de ciclos N, soportados antes de la ruptura). El número N, puede describirse a través de la curva de Wöhler, o curva SxN "Stress vs. Number”, que relaciona el nivel de esfuerzo aplicado con el número de ciclos que provocan la ruptura en el material. Para la mayoría de los materiales, la curva de Wöhler muestra la existencia de una tendencia en la reducción del número de ciclos a medida que aumenta el nivel de tensión (Dowling, 2012).
Actualmente, solo los materiales dúctiles, como el acero y las aleaciones, presentan ábacos y curvas de Wöhler bien definidas. En el caso del hormigón y otros materiales frágiles y casi frágiles, todavía no existen curvas definidas para todas las clases y tipos, ya que el desarrollo de la investigación relacionada con la fatiga solamente ha cobrado importancia en las dos últimas décadas, mientras que los estudios relacionados con las áreas de durabilidad, mecánica de la fractura y mecánica del daño han avanzado sustancialmente.
En cuanto al comportamiento del hormigón cuando sometido a cargas cíclicas, se han desarrollado trabajos mediante estudios teóricos, experimentales y/o numéricos, y se han dividido en cuanto al tipo de fatiga analizada: fatiga por tracción (Subramaniam y Shah, 2003; Chen, et al, 2017), tracción-compresión (Lü et al., 2004), compresión (Xiao et al., 2013; Lantsoght et al., 2016; Jiang et al., 2017) y flexión (Kim et al., 2013; Arora y Singh, 2016; Kasu et al., 2019; Saiani y Sinsh, 2020). La mayor parte de las investigaciones encontradas en la literatura están dirigidas a evaluar la fatiga a la flexión, donde los esfuerzos de tracción son preponderantes.
En Brasil, por ejemplo, las investigaciones están relacionadas principalmente con la fatiga por flexión en vigas o con la compresión y flexión en pavimentos de hormigón, siendo la mayoría (de las investigaciones) de carácter numérico o teórico-numérico (Baroni, 2010; Junges, 2017; Mascarenhas y Carvalho, 2019).
La principal dificultad encontrada en el estudio experimental del comportamiento de la fatiga del hormigón en Brasil está relacionada con la falta de equipos capaces de realizar ensayos cíclicos con alta velocidad de carga. Medeiros (2012), por ejemplo, ejecutó parte de su investigación en el extranjero, debido a la falta de disponibilidad, en ese momento, de máquinas y equipos de laboratorio para los ensayos de fatiga por compresión. El autor analizó experimentalmente la ganancia de resistencia a la fatiga debida a la incorporación de fibras en la matriz cementante del hormigón, comprobando también la influencia de diferentes frecuencias de carga.
A partir de ese despliegue, este trabajo tiene como objetivo investigar el comportamiento a la fatiga del hormigón con el fin de analizar la vida útil a la fatiga (VUF) de los concretos de baja (30 MPa), y alta (50 y 70 MPa) resistencia a la compresión, sometidos a diferentes condiciones de carga. El estudio experimental se desarrolló considerando la compresión cíclica, donde los ensayos se realizaron combinando tres frecuencias de carga (0.125, 0.25 y 0.5 Hz) y dos niveles de tensión máxima (50% y 70% de la resistencia a la compresión).
2. Fatiga en el hormigÓn
2.1 Degradación del material por la carga cíclica
En un cuerpo sometido a cargas cíclicas, las nucleaciones a nivel microscópico se originan con un bajo número de repeticiones debido al efecto de la fatiga en el material. La progresión de las grietas hasta su observación a nivel macroscópico es lenta, si se considera la vida a fatiga del sólido, normalmente expresada por el número de ciclos necesarios para provocar el fallo del material (N f ).
La vida útil a la fatiga (VUF) se clasifica generalmente en dos etapas: una referida a la aparición de nucleaciones en el material y otra a la propagación de grietas. En el periodo de iniciación también se observa el crecimiento microestructural de las grietas, sin embargo, en dimensiones tan insignificantes que no son consideradas en la representación o cuantificación del nivel de daño del material. A la vez, el periodo de propagación puede caracterizarse por el periodo que se refiere al desarrollo de las grietas a nivel mesoscópico. La figura 1 exhibe las diferentes fases que configuran la vida útil a la fatiga, considerando aspectos relacionados con el agrietamiento del material.
 |
||||
| Figura 1. Etapas de la VUF asociadas al agrietamiento del concreto. | ||||
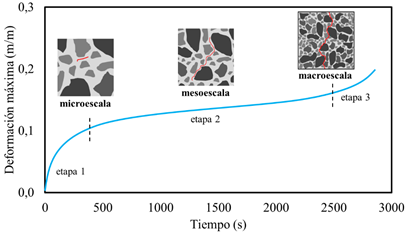
Desde la aparición de la primera microfisura hasta la ruptura del material, el daño por fatiga en el hormigón puede caracterizarse en tres etapas (Figura 2): (i) origen de la grieta, o sea, cuando la microfisura aparece a causa de la alta concentración de tensiones en puntos de discontinuidad en la estructura cristalina o, en regiones con discontinuidades preexistentes en el material; (ii) propagación de la grieta, por consecuencia de la acumulación de energía en las extremidades de las grietas existentes; y (iii) ruptura del material, que sucede de manera abrupta, debido a la naturaleza casi-frágil del material.
 |
||||
| Figura 2. Progresión de agrietamiento del concreto en función de la deformación máxima y del tiempo de ensayo en los cuerpos de prueba sometidos a cargas cíclicas. | ||||
Para predecir o supervisar la vida útil de un elemento de concreto cuando se somete a fatiga, es necesario conocer el comportamiento mecánico del material cuando se somete a ciclos de carga y descarga. Las propiedades del concreto relacionadas con la fatiga se determinan a partir de ensayos de laboratorio, en los que los datos obtenidos suelen presentarse mediante un gráfico de la tensión o la deformación específica en función del número de ciclos hasta el rompimiento, curva S-N y ε-N, respectivamente.
Existen varios modelos en la literatura para predecir la vida a la fatiga del hormigón, como se presenta en las ecuaciones (1)-(3) (Wöhler, 1960; Raithby y Galloway, 1974; Tepfers y Kutti, 1979). Sin embargo, la mayoría de los modelos tienen como directrices las curvas S-N o ε-N, obtenidas en campañas experimentales, que solo funcionan con un número reducido de casos, lo que hace inviable su empleo de manera generalizada.
 |
 |
 |
S max es la tensión máxima aplicada, f t,f es la resistencia a la tracción en la flexión estática del hormigón, N es el número de ciclos para el colapso del material, d y e son parámetros del material obtenidos por regresión de los datos, R es la relación entre la tensión mínima y la máxima, f ck es la resistencia característica del hormigón, f est es la resistencia bajo análisis (tracción, compresión o flexión) o tracción estática del hormigón.
Según Lee y Barr (2004), son muchas las razones que hacen inviable el uso de la curva de Wöhler (Ecuación (1)) de forma generalizada, siendo la principal la determinación de los parámetros a través de la regresión de datos, ya que existe una considerable dispersión en los resultados de los ensayos de fatiga del hormigón, considerando muestras del mismo lote, bajo las mismas condiciones de ensayo.
Ortega et al. (2018) informan que la gran dispersión en los resultados es consecuencia de la sensibilidad de la resistencia a la fatiga a una variedad de parámetros relacionados con el ensayo y el material, que son casi imposibles de controlar con precisión, como las condiciones de moldeo, la alineación del cuerpo de prueba en el equipo de ensayo, la imposición de las tensiones máximas y mínimas, la frecuencia de cargamento y el posicionamiento de los extensómetros o Strain Gauges.
2.2 Factores que intervienen en la vida útil a la fatiga
El estudio de la fatiga del hormigón tuvo sus primeras publicaciones a mediados de la década de 1920, con la publicación de Clemmer (1922), donde se observó que el hormigón tiene un comportamiento distinto al del acero cuando se somete a un cargamento cíclico, señalando que este mecanismo de degradación se correlacionaba con los principios de la mecánica de la fractura.
A lo largo de los últimos cien años, tras la publicación de los primeros trabajos, se han desarrollado numerosos estudios sobre la fatiga en el hormigón, cuya mayoría de ellos (hasta los años 90) se refieren a la determinación de un modelo general, que consideraba los diferentes tipos de ensayos a la fatiga: tracción directa, tracción a flexión, tracción a compresión, compresión y tracción-compresión alternada.
Según Medeiros (2012), el modo de carga influye en el comportamiento del concreto hasta su fatiga, ya que son múltiplos los factores que rigen el mecanismo de ruptura del concreto en la compresión, tracción o flexión. Además, se sabe que otros parámetros pueden influenciar la resistencia a la fatiga y vida útil, como los materiales constitutivos, las condiciones de humedad, la relación entre las tensiones mínimas y máximas (R), la frecuencia de carga, entre otros.
Raithby y Galloway (1974) analizaron la influencia de las condiciones de humedad en la determinación del número de ciclos hasta la ruptura del hormigón convencional. Los autores analizaron las condiciones del hormigón saturado, del hormigón secado al aire durante una semana (Ecuación (2)) y del hormigón secado al horno durante una semana. Los resultados encontrados coinciden con los observados por Cornelissen y Lewis (1986), donde el hormigón saturado presenta una vida útil más corta que el hormigón secado al aire, pero prácticamente igual que el hormigón secado al horno.
Tepfers y Kutti (1979) propusieron modelos para determinar la vida útil del hormigón sometido a fatiga por compresión, tracción y flexión, verificando mediante análisis estadístico que la Ecuación (3) responde a los diferentes tipos de carga. Sin embargo, Cornelissen (1984) presentó un estudio que demostraba que el modo de carga influye en el comportamiento del concreto a su fatiga, indicando que un único modelo no representaría adecuadamente el fenómeno para diferentes tipos de carga. Además, Cornelissen (1984) y Zhang et al. (1996) verificaron que los ensayos con alternancia provocan una mayor reducción en la resistencia a la fatiga que los ensayos únicamente en tracción en la flexión.
En cuanto a los materiales constituyentes, aún no se ha llegado a un consenso sobre la influencia de la relación agua/cemento (a/c) y del consumo de cemento. Tepfers y Kutti (1979) y Zhang et al. (1997) muestran que estos parámetros son indiferentes al comportamiento del hormigón sometido a fatiga por tracción o flexión, afectando únicamente a la resistencia estática del material.
En cuanto al tipo de árido utilizado, Sparks (1982) demostró que existe una fuerte correlación entre la tasa de deformación secundaria y el número de ciclos hasta la ruptura del hormigón, de modo que los concretos producidos con agregados finos tienen una vida útil más corta en comparación con los concretos con agregados convencionales (agregados de origen basáltico o granítico).
Por último, se sabe que la frecuencia de carga (f) puede tener una gran influencia en el comportamiento a la fatiga del hormigón, y aún más, se sabe también que, al aumentar la frecuencia, la vida útil a la fatiga aumenta. Sin embargo, la mayoría de los trabajos existentes en la literatura que corroboran esta afirmación fueron desarrollados para altas frecuencias (f > 1.0) y para tensiones máximas que varían entre el 75% y el 95% de la resistencia estática (Zhang et al., 1996). Jansen (1996) observó que para tensiones máximas inferiores al 75% de la resistencia estática del hormigón, las frecuencias entre 1 y 15 Hz tienen poca influencia en la resistencia a fatiga, y más, se sabe que una reducción de 100 veces en la frecuencia resulta en una reducción de 10 a 30 veces en el número de ciclos.
3. CampaÑa experimental
La metodología utilizada en este trabajo se define en cinco etapas cuyo objetivo se centra en la evaluación de la vida útil a la fatiga de cuerpos de prueba cilíndricos bajo compresión cíclica.
 |
||||
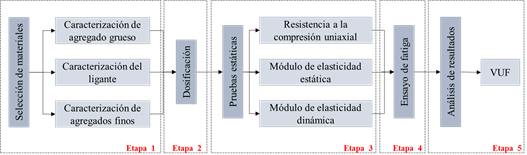
| Figura 3. metodología de trabajo | ||||
Las cinco actividades desarrolladas en el trabajo se presentan en la Figura 3 y se refieren a: i) selección y caracterización de los materiales; ii) dosificación y moldeo del hormigón; iii) ensayos para definir las propiedades mecánicas del material; iv) ensayo de fatiga por compresión; y v) análisis de los resultados obtenidos. Cada una de estas actividades se describe en detalle a continuación.
3.1 Selección y caracterización de materiales
En este estudio, para la producción de hormigón, se utilizó como ligante el cemento Portland CP II Z 32, compuesto con puzolana y con 32 MPa de resistencia a la compresión. La masa específica (3.06 g/cm³) y la superficie específica (3965.00 cm²/g) de este cemento se determinaron según la NBR NM 23:2001 (ABNT, 2001) y la NBR 16372:2015 (ABNT, 2015), respectivamente.
Se utilizaron arena de cuarzo y grava 0 de origen basáltico como agregados finos y gruesos, respectivamente. Para la caracterización de los agregados (Tabla 1), se realizaron las pruebas de composición granulométrica, masa específica, masa unitaria, absorción de agua y módulo de finura.
En cuanto a la composición granulométrica del agregado fino, se constató que los dos lotes analizados se ajustan a los límites granulométricos recomendados por la NBR 7211 (ABNT, 2009) para la arena fina. En cuanto a los agregados gruesos, los resultados demostraron el tamaño máximo característico de 9,5 mm, correspondiente a la grava 0.
| Tabla 1. Caracterización física de los agregados | ||||||||||||||
| Propriedades | Agregado fino | Agregado grueso | Normas utilizadas | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Massa unitaria (kg/m3) | 1390 | 1401 | NBR NM 45: 2006 | |||||||||||
| Massa especifica (kg/m3) | 2520 | 2590 | NBR NM 53: 2003 | |||||||||||
| Absorción (%) | 0.22 | 1.45 | NBR NM 53, 2003 | |||||||||||
| Módulo de finura | 1.46 | - | NBR NM 248 2003 | |||||||||||
Para los hormigones de la clase C50 y C70, fue necesario emplear aditivos superplastificantes, que están compuestos por polímeros orgánicos, comúnmente usados como reductores de agua, que permiten reducir el factor agua/cemento y dispersar las partículas de cemento, mejorando así la fluidez de las mezclas.
Por último, hay que relatar que en todos los hormigonados se utilizó agua potable de la red de suministro local, por lo que no fue necesario controlar su aceptación.
3.2 Dosificación y producción de hormigón
Para la definición del programa experimental, se produjeron concretos considerando tres composiciones diferentes, siendo una para un hormigón convencional de baja resistencia, con resistencia característica a la compresión igual a 30 MPa (C30) y dos para hormigones de alta resistencia, con 50 (C50) y 70 MPa (C70).
Para la dosificación se utilizó el método ABCP (Rodrigues, 1984) con un asentamiento fijado en (120 ± 20) mm. Las dosificaciones iniciales se hicieron para que la composición de los materiales proporcionara un concreto con las resistencias deseadas. La tabla 2 muestra el consumo de materiales para cada una de las dosificaciones producidas.
En total, se produjeron 126 cuerpos de prueba cilíndricos de 5 cm de diámetro y 10 cm de altura, 42 cuerpos de prueba para cada uno de los tres lotes. Los hormigones se moldearon en una mesa vibratoria y se sometieron a un curado con temperatura y humedad controladas hasta el momento de los ensayos, a los 28 y 90
| Tabla 2. Consumo de materiales. | ||||||||||||||
| Material | Consumo de materiales en kg/m3 | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C30 | C50 | C70 | ||||||||||||
| Cemento (CP II Z 32) | 353.96 | 395.55 | 553.43 | |||||||||||
| Agregado fino | 800.44 | 1000.76 | 853.92 | |||||||||||
| Agregado grueso | 1023.68 | 819.96 | 826.75 | |||||||||||
| Agua | 184.19 | 166.37 | 168.92 | |||||||||||
| Aditivo | - | 2.38 | 4.41 | |||||||||||
| Relación agua/cemento | 0.52 | 0.42 | 0.3 | |||||||||||
días.
3.3 Ensayos con cargas estáticas
Para los ensayos de caracterización del hormigón con cargamento estático, se utilizaron dieciocho cuerpos de prueba, de los cuales seis fueron empleados en los ensayos de resistencia a la compresión a los 7 días, seis a los 28 días, seis para el análisis de resistencia y determinación del módulo de elasticidad estático y dinámico a los 90 días (período en el que ocurrieron los ensayos de compresión cíclica). Los ensayos se realizaron de acuerdo con las normas NBR 5739 (ABNT, 2007), NBR 8522 (ABNT, 2017) y ASTM E1876 (2015).
En este trabajo se ha considerado el módulo de elasticidad dinámico porque es una propiedad que representa el comportamiento del hormigón cuando se somete a cargas dinámicas. Los ensayos de módulo de elasticidad dinámico se realizaron mediante la técnica de excitación por impulsos (TEI), una técnica no destructiva, que permite utilizar el cuerpo de prueba en otro ensayo. Este ensayo se realizó con el fin de determinar la variación del módulo de elasticidad y el daño correspondiente, evaluado durante la prueba de fatiga.
El módulo de elasticidad dinámico y su respectivo módulo estático, obtenidos mediante la formulación de Popovics (2008) (Ecuación (4), se midieron en seis cuerpos de prueba antes del inicio de los ensayos de resistencia a la compresión a los 90 días.
 |
E c es el módulo de elasticidad estático (en Pa), ρ es la densidad del hormigón (en kg/m³), E d es el módulo de elasticidad dinámico (en Pa).
3.4 Ensayos de fatiga
Para los ensayos de fatiga se usaron cuerpos de prueba cilíndricos de 10 cm de altura y 5 cm de diámetro, sometidos a compresión cíclica en una máquina servohidráulica Instron 8805 con capacidad máxima de ± 1500 kN. La elección de los cuerpos de prueba se hizo buscando una dimensión en la cual la velocidad máxima de carga utilizada en los ensayos fuera inferior a la velocidad máxima soportada por la máquina (80 kN/s) y que aún representara adecuadamente el comportamiento del material. Como justificación del tamaño del cuerpo de prueba, se indica el estudio experimental realizado por Saini et. al. (2015) que observó que, para la fatiga por compresión, el diámetro del cuerpo de prueba tiene influencia superior a la relación altura/diámetro del cuerpo de prueba y que un diámetro igual o superior a 5 cm es suficiente para evaluar y/o ensayar cuerpos de prueba de concreto bajo compresión cíclica. Saini et. al. (2015) informan aún que hay que utilizar un cuerpo de prueba con una relación entre el diámetro del cuerpo de prueba y el diámetro máximo del agregado superior a 5.
La máquina servohidráulica usada tiene un control electrónico que recibe señales analógicas de hasta seis canales diferentes, ya sea de carga, desplazamiento o lectura de una galga extensométrica. La figura 4.a muestra una vista general de la posición de dos galgas extensométricas del tipo doble roseta (con direcciones que varían en 90º) y dos LVDTs, utilizadas en los cuerpos de prueba. Ya en la figura 4.b se enseña el esquema de carga cíclica empleada.
 |
||||
| Figura 4. Esquema (a) de la instrumentación y (b) de la carga cíclica. | ||||
Los ensayos de fatiga se configuraron mediante el control de la carga. Como se presenta en la Figura 4.b, la definición de las cargas máximas y mínimas se realizó considerando dos configuraciones distintas, una para la carga máxima del 50% de la resistencia a la compresión (f c ) y otra para el 70% de f c , considerando en ambos casos, una carga mínima de 0 kN, lo que configura relaciones entre la tensión mínima y máxima (R) de 0 para ambos casos.
Se analizaron cuatro cuerpos de prueba para determinar el número medio de ciclos, necesarios para la ruptura por fatiga en compresión, para los dieciocho casos estudiados. Los dieciocho casos se refieren a la combinación de tres frecuencias de carga (0.125, 0.25 y 0.5 Hz), dos niveles de tensión máxima (50% y 70% f c ) y tres clases de resistencia a la compresión (30, 50 y 70 MPa).
Para facilitar la lectura de los resultados, se utilizó la nomenclatura C#S#F#, donde C# se refiere a la clase de resistencia del hormigón (C30 para 30 MPa, C50 para 50 MPa o C70 para 70 MPa), S# se refiere a la tensión máxima adoptada (S5 para el 50% y S7 para el 70%) y F# describe la frecuencia de carga (F125 para 0.125 Hz, F25 para 0.25 Hz y F5 para 0.5 Hz).
4. Resultados
4.1 Caracterización
La caracterización de las propiedades mecánicas de los hormigones empleados en el estudio experimental se realizó mediante ensayos de resistencia a la compresión del concreto (f c ), módulo de elasticidad estático (E c ) y módulo de elasticidad dinámico (E d ).
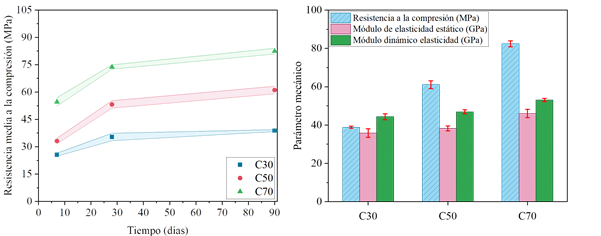
En cuanto a la determinación de la resistencia a la compresión del concreto, se realizaron ensayos de compresión estática en seis cuerpos de prueba para cada una de las dosificaciones. Los ensayos se realizaron a los 7, 28 y 90 días, en los que el hormigón permaneció en curado con la temperatura y la humedad controladas a 25°C y 75%, respectivamente. En la figura 5.a se presenta la resistencia media a la compresión de los concretos, considerando los tres períodos de tiempo evaluados. Las áreas sombreadas del gráfico representan el rango de valores referentes a la media ± desviación estándar de la muestra.
En la Figura 5.b se presentan los promedios de los resultados obtenidos para todas las propiedades mecánicas evaluadas en 90 días. Los datos se ordenaron de forma que se indicara la resistencia a la compresión, el módulo de elasticidad estático y el módulo de elasticidad dinámico. Además, se presentan los desvíos estándar de las propiedades evaluadas.
Los resultados de la caracterización de las propiedades mecánicas indican que los concretos dosificados presentan una resistencia a la compresión media, a los 28 días, adecuada a la clase de resistencia para la que fueron dosificados, siendo las resistencias medias de 35.35 MPa para la dosificación C30, 53.21 MPa para la dosificación C50 y 73.74 MPa para la dosificación C70.
 |
||||
| Figura 5. Medias y desviaciones de (a) la resistencia a la compresión a los 7, 28 y 90 días, y (b) la resistencia a la compresión y el módulo de elasticidad estático y dinámico a los 90 días. | ||||
En cuanto al módulo de elasticidad estático, se observó una pequeña variación de su valor al variar la resistencia a la compresión del material. Este resultado corrobora los estudios realizados por Vasconcellos (2018) y Graeff y Prudêncio Jr. (2016), donde se ha comprobado mediante estudios experimentales que un cambio significativo en la resistencia a la compresión del hormigón no configura necesariamente un cambio significativo en el valor del módulo de elasticidad, siendo importante evaluar otros parámetros, como la relación agua/cemento, el contenido de pasta de cemento y la proporción de agregados y pasta.
Con el propósito de analizar los valores obtenidos para el módulo estático y dinámico, se utilizó la Ecuación (4) para evaluar si el módulo de elasticidad estático, obtenido experimentalmente, se aproximaba al módulo de elasticidad estático estimado por el módulo dinámico. Aplicando la Ecuación (4), para los concretos C30, C50 y C70, se obtuvieron módulos estáticos iguales a 35.50, 39.27 y 45.65 GPa, respectivamente, mientras que los valores experimentales medios fueron 35.84, 38.29 y 46.05 GPa. La diferencia porcentual entre los valores obtenidos en la predicción y los medidos experimentalmente fue de 0.94, 2.55 y 0.86% para los concretos C30, C50 y C70, respectivamente. Este resultado denota el nivel de precisión de la Ecuación (4) en la predicción del módulo de elasticidad estático del hormigón, considerando los resultados obtenidos mediante la Técnica de Excitación por Impulsos (TEI).
4.2 Vida útil a la fatiga
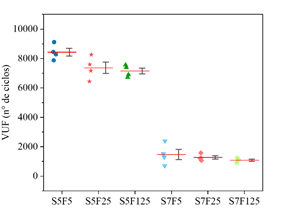
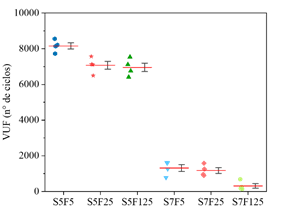
Dados los diferentes escenarios de carga considerados en la campaña experimental, y considerando las propiedades mecánicas medidas y mostradas en las Figuras 5.a y 5.b, las Figuras 6-8 presentan el número de ciclos (VUF) que cada una de las cuatro muestras ensayadas, por compresión cíclica, resistió antes de suceder la ruptura. Los resultados se ordenaron para presentar el número de ciclos necesarios para provocar el fallo de cada uno de los cuatro cuerpos de prueba (VUF) y la media de los valores obtenidos en cada lote de muestreo (línea roja). En los gráficos también se representan recuadros que contienen los percentiles primero y tercero.
Con el propósito de evaluar la viabilidad de los modelos clásicos para predecir la vida útil a la fatiga del hormigón, se emplearon las Ecuaciones (2) y (3) para estimar la VUF de los hormigones analizados en este trabajo. Los resultados obtenidos se compararon con los observados experimentalmente.
Aplicando la Ecuación (2), la VUF predicha fue de 38 millones de ciclos para el hormigón sometido a la tensión máxima del 50% de f c , y de 200 mil ciclos para el hormigón sometido a la tensión máxima del 70% de f c , siendo estos valores muy superiores a los resultados mostrados en las Figuras 6,7,8. Ya usando la Ecuación (3), el VUF predicho fue inferior al valor obtenido por la ecuación (2), y se calculó un VUF de 19 millones de ciclos para el hormigón sometido a la tensión máxima del 50% de f c , y de 23 mil ciclos para el hormigón sometido a la tensión máxima del 70% de f c , resultado también muy superior a los obtenidos experimentalmente. Cabe mencionar que los resultados obtenidos por las formulaciones no dependen de la clase de resistencia del material y tampoco de las condiciones de cargamento.
Así, los resultados obtenidos por las Ecuaciones (2) y (3) denotan la importancia de estudiar el comportamiento y la vida útil a la fatiga del hormigón sometido a cargas cíclicas, con la finalidad de entender mejor el comportamiento del material y proponer modelos que incorporen en sus formulaciones parámetros relacionados a las condiciones de carga y de rigidez del material.
 |
||||
| Figura 6. VUF de los concretos C30. | ||||
 |
||||
| Figura 7. VUF de los concretos C50. | ||||
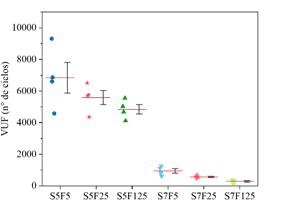 |
||||
| Figura 8. VUF de los concretos C70. | ||||
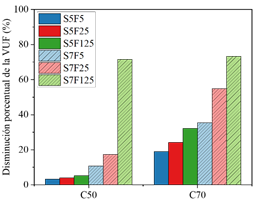 |
||||
| Figura 9. Variación de la vida útil a la fatiga de los concretos C50 y C70 con relación al C30. | ||||
Evaluando la Figura 6,7,8, es posible observar que incluso para bajas frecuencias (f <1,0), el número de ciclos necesarios para llevar los cuerpos de prueba a su ruptura disminuye a medida que la frecuencia de carga disminuye, comportamiento que también se observa en los trabajos de Zhang et al. (1996) y Medeiros (2012). Además, se observa que este comportamiento se presenta independientemente del nivel de tensión máxima aplicada (50% o 70% de f c ), a diferencia de lo observado por Jansen (1996), donde el autor reporta una pequeña o casi inexistente influencia de la frecuencia en la vida útil a la fatiga de hormigones con tensiones máximas inferiores al 75% de la resistencia a la compresión.
Corroborando a los resultados encontrados en este trabajo, el estudio experimental realizado por Kim y Kim (1996), señala que la vida útil a la fatiga del hormigón disminuye a medida que aumenta la tensión máxima aplicada y que esta característica es más evidente en el hormigón de alta resistencia.
Con el fin de evaluar la influencia de la resistencia a la compresión del hormigón junto con la frecuencia de carga y el nivel de tensión máxima en la resistencia a la fatiga del material, la Figura 9 muestra un gráfico que contiene la disminución porcentual de la vida útil a la fatiga (VUF) de los concretos de lotes C50 y C70, en relación con la VUF medida en los concretos de lotes C30.
Al analizar los resultados mostrados en las Figuras 6-9, se observa una relación positiva entre la resistencia a la compresión del hormigón y la vida útil a la fatiga, y esta relación es más evidente cuando se evalúa el hormigón con una resistencia superior a 50 MPa (hormigón de alta resistencia). La influencia de la resistencia a la compresión en la vida útil a la fatiga fue investigada en los trabajos de Al-Gadhib et al. (2000) y Kessler-Kramer et al. (2003), donde los autores indican que la fragilidad que adquiere el material al ganar resistencia puede estar directamente relacionada con su comportamiento a la fatiga, ya que ésta se define por la degradación del material al ser sometido a cargas cíclicas.
Considerando los resultados mostrados en la Figura 9 y considerando que los concretos de los lotes C50 y C70 presentan, respectivamente, resistencias medias superiores al 57,37% y al 112,33%, se puede inferir que la reducción de la VUF es mayor para los hormigones sometidos al mayor nivel de tensión máxima aplicada (70% de f c ), independientemente de la resistencia del material. Además, se observó que las reducciones de la VUF aumentan con la disminución de la frecuencia de la carga adoptada.
Dados los resultados presentados en esta sección, se infiere un crecimiento de la vida útil a la fatiga al aumentar la frecuencia de carga, mientras sea mantenido el mismo nivel de tensión aplicado al material. Además, se observa que este comportamiento se visualiza mejor cuando se analiza el hormigón de alta resistencia a la compresión.
Una posible justificación encontrada por Chen et al. (2017) para explicar este fenómeno se refiere a que, en la aplicación de cargas cíclicas, el hormigón deja de tener su comportamiento definido por las propiedades estáticas y pasa a estar mejor representado por las propiedades dinámicas, que a su vez son superiores a las estáticas.
Por último, se comenta que durante los ensayos no se observó un modo de ruptura característico del hormigón bajo compresión cíclica. Sin embargo, como ocurre en los ensayos de compresión estática, la ruptura del material se configuró de forma más abrupta en los hormigones con mayor resistencia a la compresión. Además, cabe destacar que el modo abrupto observado en la ruptura del hormigón de alta resistencia fue mayor en los ensayos cíclicos que en los de compresión estática, lo que indica que el nivel de fragilidad del material es un parámetro influyente en el comportamiento mecánico del hormigón sometido a cargas cíclicas.
5. Conclusiones
El comportamiento mecánico del hormigón sometido a compresión cíclica fue investigado experimentalmente en este trabajo mediante la evaluación de la vida útil a la fatiga, considerando hormigones de tres clases de resistencia y sometidos a diferentes condiciones de carga. A la hora de evaluar los resultados obtenidos, se pueden indicar las siguientes consideraciones:
Finalmente, se menciona que este es el primer estudio experimental desarrollado por el grupo de investigación, y que en el futuro se realizarán nuevos experimentos para ampliar el análisis a otros niveles de tensión, frecuencia de carga y resistencia a la compresión del material. Como trabajo futuro, también se pretende proponer curvas S-N para el hormigón sometido a compresión cíclica, así como formulaciones que contribuyan en el análisis del proyecto a fatiga de elementos de concreto.
6. Agradecimientos
Los autores agradecen por el apoyo brindado a la investigación a los órganos brasileños: Consejo Nacional de Desarrollo Científico y Tecnológico (Conselho Nacional de Desenvolvimento Científico e Tecnológico - CNPq) (CNPq 141078/2018, 310564/2018-2 y 428762/2018-2) y la Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES código 001).
Referencias
Associação Brasileira de Normas Técnicas (2001). NBR NM 23: Agregados - Determinação da composição granulométrica. Rio de Janeiro.
Associação Brasileira de Normas Técnicas (2003). NBR NM 248: Agregados - Determinação da composição granulométrica. Rio de Janeiro.
Associação Brasileira de Normas Técnicas (2006). NBR NM 45: Agregados - Determinação da massa unitária e do volume de vazios. Rio de Janeiro.
Associação Brasileira de Normas Técnicas (2007). NBR 5739: Concreto - Ensaios de compressão de corpos-de-prova cilíndricos. Rio de Janeiro.
Associação Brasileira de Normas Técnicas (2009). NBR 7211: Agregados para concreto - Especificações. Rio de Janeiro.
Associação Brasileira de Normas Técnicas (2008). NBR 8522: Concreto - Determinação do módulo estático de elasticidade à compressão. Rio de Janeiro.
Associação Brasileira de Normas Técnicas (2009). NBR NM 53: Agregado graúdo - Determinação da massa específica, massa específica aparente e absorção de água. Rio de Janeiro.
Associação Brasileira de Normas Técnicas (2015). NBR 16372: Cimento Portland e outros materiais em pó ― Determinação da finura pelo método de permeabilidade ao ar (método de Blaine). Rio de Janeiro.
Al-Gadhib, A. H., Baluch, M., Shaalan, A., Khan, A. (2000), Damage model for monotonic and fatigue response of high strength concrete. International Journal of Damage Mechanics, v. 9, n. 1, p. 57-78. https://doi.org/10.1177/105678950000900105
Arora, S., Singh, S. P. (2016), Analysis of flexural fatigue failure of concrete made with 100% Coarse Recycled Concrete Aggregates. Construction and Building Materials, v. 102, n. 1, p. 782-791. https://doi.org/10.1016/j.conbuildmat.2015.10.098
ASTM International (2015), ASTM E1876: Standard Test Method for Dynamic Young’s Modulus, Shear Modulus, and Poisson’s Ratio by Impulse Excitation of Vibration.
Baroni, H. J. M. (2010), “Simulação da vida útil de fadiga do concreto em vigas de tabuleiro de pontes em função do fluxo de veículos pesados”. Tese (Doutorado). Programa de Pós-Graduação em Engenharia Civil. Universidade Federal do Rio Grande do Sul. Porto Alegre.
Chen, X., BU, J., Fan, X., Lu, J., Xu, L. (2017), Effect of loading frequency and stress level on low cycle fatigue behavior of plain concrete in direct tension. Construction and Building Materials, v. 133, p. 367-375. https://doi.org/10.1016/j.conbuildmat.2016.12.085
Clemmer, H. F. (1922), Fatigue of concrete. Proceedings, American Society for Testing and Materials. v. 22, n. 2, p. 408-419.
Cornellissen, H. A. W. (1984), Fatigue failure of concrete in tension. Heron, v. 29, n. 4, p. 2-67.
Cornelissen, H. A. W., Lewis, M. (1986) “Fatigue experiments for the design of plain concrete pavements” in: Workshop on Theoretical Design of Concrete Pavements, CROW-PIARC-CEMBUREAU, Report 1, Holanda.
Dowling, N. E. (2012), “Mechanical behavior of materials: Engineering methods for deformation, fracture, and fatigue”. Practice Hall, 4th edition, United States.
Graeff, E.; Prudêncio Jr., L. R. (2016). Determinação do módulo de elasticidade dos concretos da central de Itajaí da Maxmohr. [S.l.]: Relatório técnico.
Jansen A. (1996), “Research to fatigue behaviour of topping on prefabricated concrete girders”. Thesis (Master). Delft University of Technology. Holanda.
Jiang, C., Xianglin, G., Huang, Q., Zhang, W. (2017), Deformation of concrete under high-cycle fatigue loads in uniaxial and eccentric compression. Construction and Building Materials, v. 141, p. 379-392. https://doi.org/10.1016/j.conbuildmat.2017.03.023
Junges, P. (2017), “Análise de fadiga em pontes curtas de concreto armado a partir de dados de sistemas B-WIM”. Tese (Doutorado). Centro Tecnológico: Programa de Pós-Graduação em Engenharia Civil. Universidade Federal de Santa Catarina. Florianópolis.
Kasu, S. R., Deb, S., Mitra, N., Muppireddy, A. R., Kusam, S. R. (2019), Influence of aggregate size on flexural fatigue response of concrete. Construction and Building Materials, v. 229, p. 1-9. https://doi.org/10.1016/j.conbuildmat.2019.116922
Kessler-Kramer, C., Mechtcherine, V., Mueller, H. S. (2003), “Failure of normal and high strength concrete under monotonic and cyclic tensile loading” in: Brittle Matrix Composites 7. Woodhead Publishing. p. 277-286. https://doi.org/10.1533/9780857093103.277
Kim, J. K., Kim, Y. Y. (1996), Experimental study of the fatigue behavior of high strength concrete. Cement and Concrete Research, v. 26, n. 10, p. 1513-1523.
Kim, J., Yi, C., Lee, S. J., Zi, G. (2013), Flexural fatigue behaviour of concrete under uniaxial and biaxial stress. Magazine of Concrete Research, v. 65, n. 12, p. 757-764. https://doi.org/10.1016/0008-8846(96)00151-2
Lantsoght, E. O. L., Van Der Veen, C., Boer, A. (2016), Proposal for the fatigue strength of concrete under cycles of compression. Construction and Building Materials, v. 107, p. 138-156. https://doi.org/10.1016/j.conbuildmat.2016.01.007
Lee, M. K., Barr, B. I. G. (2004), An overview of the fatigue behavior of plain and fiber reinforced concrete. Cement and Concrete Composites. v. 26, p. 299-305. https://doi.org/10.1016/S0958-9465(02)00139-7
Lü, P., Li, Q., Song, Y. (2004), Damage constitutive of concrete under uniaxial alternate tension-compression fatigue loading based on double bounding surfaces. International Journal of Solids and Structures, v. 41, p. 3151-3166. https://doi.org/10.1016/j.ijsolstr.2004.01.026
Mascarenhas, F. Jr. R., Carvalho, R. C. (2019), Vida útil à fadiga da armadura longitudinal de vigas de pontes de concreto armado frente ao tráfego real de veículos pesados. Revista AlCONPAT, v. 9, n. 3, p. 303-319. https://doi.org/10.21041/ra.v9i3.375
Medeiros, A. (2012), “Estudo do comportamento à fadiga em compressão do concreto com fibras”. Tese (Doutorado). Departamento de Engenharia Civil: Programa de Pós-graduação em Engenharia Civil. Pontifícia Universidade Católica do Rio de Janeiro. Rio de Janeiro.
Ortega, J. J., Ruiz, G., Yu, R. C., Afanador-García, N., Tarifa, M., Poveda, E., Zhang, X., Evangelista JR., F. (2018), Number of tests and corresponding error in concrete fatigue. International journal of fatigue, v. 116, p. 210-219. https://doi.org/10.1016/j.ijfatigue.2018.06.022
Popovics, J. S. (2008) “A study of static and dynamic modulus of elasticity of concrete”. University of Illinois, Urbana, IL. ACI-CRC Final Reports.
Raithby, K. D., Galloway, J. W. (1974), “Effects of moisture condition, age, and rate of loading on fatigue of plain concrete” in: ABELES Symposium: Fatigue of Concrete. ACI Publication, v. 41, p. 15-34.
Rodrigues, P. P. F. (1984), “Parâmetros de dosagem do cocreto.” São Paulo: ABCP, 1984.
Saini, B. S., Singh, S. P. (2020), Flexural fatigue life analysis of self-compacting concrete containing 100% coarse recycled concrete aggregates. Construction and Building Materials, v. 253, p. 1-13. https://doi.org/10.1016/j.conbuildmat.2020.119176
Sparks, P. R. (1982), Influence of rate of loading and material variability on the fatigue characteristics of concrete. ACI Journal, v. 75, n. 16, p. 331-342.
Subramaniam, K. V., Shah, S. P. (2003), Biaxial tension fatigue response of concrete. Cement and Concrete Composites, v. 25, n. 6, p. 617-623. https://doi.org/10.1016/S0958-9465(02)00075-6
Tepfers, R., Kutti, T. (1979), Fatigue strength of plain, ordinary and lightweight concrete. ACI Journal, v. 76, n. 29, p. 635-652.
Vasconcellos, A. T. D. (2018). “Estudo da variabilidade do módulo de elasticidade de concretos produzidos com diferentes tipos de agregados graúdos”. Dissertação (Mestrado). Departamento de Engenharia Civil: Programa de Pós-graduação em Engenharia Civil. Universidade Federal de Santa Catarina. Santa Catarina.
Xiao, J., Li, H., Yang, Z. (2013), Fatigue behavior of recycled aggregate concrete under compression and bending cyclic loadings. Construction and Building Materials, v. 38, p. 681-688. https://doi.org/10.1016/j.conbuildmat.2012.09.024
Zhang, B., Phillips, D. V., Wu, K. (1996), Effect of loading frequency and stress reversal of fatigue life of plain concrete. Magazine of Concrete Research, v. 48, n. 177, p. 361-375. https://doi.org/10.1680/macr.1996.48.177.361
Zhang, B., Phillips, D. V., Wu, K. (1997), Further research on fatigue properties of plain concrete. Magazine of Concrete Research, v. 49, n. 78, p. 241-252. https://doi.org/10.1680/macr.1997.49.180.241
