Investigación Aplicada

https://doi.org/10.21041/ra.v11i2.515

Verificación de seguridad de la fatiga de puentes en hormigón armado según ABNT NBR 6118:2014

Safety verification of fatigue of a reinforced concrete bridge according to ABNT NBR 6118 2014

Verificação de Segurança à fadiga de pontes em concreto armado conforme ABNT NBR 6118, 2014.

M. D. Rossato^{1 *} , G. S. Munhoz² , R. B. P. dos Santos¹, L. M. O. Scoz¹

¹ Departamento de Engenharia Civil, Escola do Mar, Ciência e Tecnologia, Universidade do Vale do Itajaí - UNIVALI, Itajaí, Brasil.

² Departamento de Construção Civil, Universidade Federal do Paraná - UFPR, Curitiba, Brasil.

^* Autor de contacto: mateusrossato.engcivil@gmail.com

Recepción: 16 de septiembre de 2020.
Aceptación: 20 de enero de 2021.
Publicación: 01 de mayo de 2021.

Citar como: Rossato, M. D., Munhoz, G. S., P. dos Santos, R. B., Scoz, L. M. (2021), "Verificación de seguridad de la fatiga de puentes en hormigón armado según ABNT NBR 6118:2014.", Revista ALCONPAT, 11 (2), pp. 109 – 123, DOI: https://doi.org/10.21041/ra.v11i2.515

Resumen
En este estudio, se verificó la seguridad a la fatiga de un puente proyectado en 1987 según la normativa brasileña vigente. Se construyó un modelo estructural para determinar y verificar la sección más crítica considerando el modelo estándar brasileño y el espectro de vehículos en la literatura. Según el método de variación de esfuerzos, se concluye que el hormigón sometido a compresión cumple con los criterios, pero la sección de acero no es suficiente para resistir los esfuerzos cortantes y de flexión. Por la regla de Palmgren-Miner, la vida útil a la fatiga de las armaduras sometidas a flexión es de 13,91 años. Es necesario un análisis más detallado de la estructura y del espectro de carga para confirmar estos resultados.
Palabras clave: fatiga, puente, regla de Palmgren-Miner, vida útil.

Abstract
In this case study, the fatigue security of a bridge designed in 1987 was examined considering the current Brazilian standard. A structural model was developed to determine and verify fatigue security in the most critical section considering the Brazilian Load Model and the literature’s vehicle spectrum. According to the stress variation method, it concludes that the concrete submitted to compression meets the minimum criteria, but the steel section is not enough to resist shearing and flexural stresses. Pursuant to the Palmgren-Miner rule, the fatigue service life of the reinforcement’s bars under flexural stress is 14,91 years. A more detailed structural analysis of the bridge and the vehicle spectrum is necessary to confirm these results.
Keywords: fatigue, bridge, Palmgren-Miner rule, service life.

Resumo
Nesse estudo de caso, a segurança à fadiga de uma ponte projetada em 1987 foi verificada segundo a norma vigente brasileira. Elaborou-se um modelo estrutural para determinar e verificar a seção mais crítica considerando o trem-tipo e o espectro de veículos da literatura. Segundo o método de limitação de variação de tensões, conclui-se que o concreto sujeito à compressão atende aos critérios, mas a área de aço não é suficiente para combater os esforços cortante e de flexão. Pela regra de Palmgren Miner, a vida útil à fadiga nas armaduras sujeitas à flexão é de 14,91 anos. Uma análise mais detalhada da estrutura e do espectro de veículos é necessária para reiterar tais resultados.
Palavras-chave: fadiga, ponte, regra de Palmgren-Miner, vida útil.

1. IntroducciÓn

En Brasil, el transporte de bienes y personas es realizado, mayoritariamente, por medio de una vasta red de carreteras, con aproximadamente 1,7 millones de kilómetros de extensión. El movimiento de cargas en esta forma corresponde al 61% da matriz nacional de transportes (CNT, 2018). En este contexto, (Baroni, 2010) defiende que las obras de arte especiales (OAEs) - puentes y viaductos - son elementos fundamentales del sistema de transportes, y asegurar su funcionalidad, seguridad y durabilidad es de suma importancia.

En las últimas décadas, la falta de políticas de mantenimiento y reparación de las OAEs en Brasil ha contribuido a acelerar el proceso de desgaste y deterioro de esas estructuras. Gran parte de los puentes brasileños fue construida entre los años 50 y 70 y, por tanto, proyectadas por normas que no preveían las cargas, ni la intensidad del tráfico existentes actualmente (Silva et.al., 2018).

Los principales daños que comprometen el desempeño de las OAEs están relacionados con la corrosión, el impacto físico y la erosión de cimentaciones. Entretanto, (Fathalla et.al., 2018) apuntan que la vida útil de puentes y viaductos también está directamente asociada a las variaciones cíclicas de tensión debido al tráfico de vehículos. (Hobbacher et.al., 2016) apunta que después de un determinado número de ciclos de carga-descarga, se produce la formación y la propagación de fisuras que pueden llevar al colapso de la estructura por fatiga. (Gao et.al., 2020) estudiaron la vida útil a la fatiga (VUF) de puentes con estructuras mistas acero-concreto y observaron que, en ese caso, la resistencia del concreto tiene poco impacto en la determinación de la VUF. Eso fue reiterado por (Santos, 2013), que probó que el colapso por fatiga puede acontecer con tensiones inferiores al límite elástico del conjunto acero-concreto.

La norma (ABNT NBR 6118, 2014) es utilizada para evaluar los daños en estructuras de concreto debido a las acciones cíclicas. Esto describe los criterios que deben ser adoptados para la verificación del estado límite último a la fatiga (método de vida ilimitada) y del estado límite de servicio. En ese caso, la verificación a la fatiga por medio de la limitación de tensiones es recomendada, haciendo uso de las cargas presentes en la (ABNT NBR 7188, 2013).

La carga propuesta por la norma brasileña (ABNT NBR 7188, 2013), que aborda las cargas móviles para puentes de carreteras y que substituyó a la (ABNT NBR 7188, 1984), no presenta configuraciones sobre el tráfico de vehículos reales, sino una carga hipotética, denominada tren estándar brasileño. Además de eso, es prevista una carga uniformemente distribuida por unidad de área, con el objetivo de representar el paso de vehículos leves o multitud. Excepcionalmente, en caso que el espectro de cargas esté disponible, se puede utilizar la regla de Palmgren-Miner, que también permite determinar la vida útil de la estructura a la fatiga. Según ese método, se supone que los daños a la fatiga se acumulan linealmente con el número de ciclos siendo esos daños denominados, conforme (Fan y Sun, 2019), como el proceso de deterioro que culmina con la reducción del área resistente de la sección transversal.

Ese estudio fue desarrollado con el objetivo de verificar la seguridad a la fatiga de un puente proyectado en 1987 conforme la (ABNT NBR 6118, 2014). Fueron utilizados dos métodos, limitación de variación de tensiones y vida útil a la fatiga. Para esto, se estudió la situación más crítica de la estructura - la viga longitudinal en el medio del vano central.

2. ContextualizaciÓn

2.1. El mecanismo de fatiga en el deterioro de puentes

De acuerdo con (Yadav y Thapa, 2020), la fatiga es un mecanismo de falla estructural que ocurre en un material sometido a variaciones de tensiones repetitivas, o sea, que oscilan de forma intermitente durante un determinado intervalo de tiempo. El conjunto de etapas de carga y descarga es denominado ciclo. Varios ciclos culminan con el surgimiento de microfisuras o con la propagación de microfisuras preexistentes, pudiendo causar el colapso de la estructura (Cervo, 2004). Cuanto mayor sea la magnitud de las cargas intermitentes, menor será el número de ciclos necesarios para romper la estructura (BT/PCC, 2000).

Los puentes y los viaductos son estructuras sujetas al fenómeno de fatiga por la acumulación de daños causados por la actuación de ciclos no uniformes de variación de tensión ocasionados por el paso de vehículos con diferentes características. La verificación de ese fenómeno en estructuras de obras de arte especiales, principalmente en situaciones de tráfico intermitente, es esencial para garantizar la seguridad estructural (Santos e Pfeil, 2014).

(Callister William, 2008) afirman que la ruptura por fatiga es de naturaleza frágil, o sea, existe poca (o ninguna) deformación plástica generalizada. De modo general, el colapso ocurre con la propagación de fisuras, y con la superficie de fractura perpendicular a la dirección de aplicación de la tensión. Sin embargo, en el ámbito del concreto, el (Comité Euro-International du Béton, 1988) defiende que no existe colapso exclusivamente por fatiga. En ese caso, la ruptura de las estructuras de concreto ocurre debido al deterioro progresivo de las fisuras causadas por la carga cíclica.

Considerando las estructuras en concreto armado, (Meneghetti, 2007) comprobó que la fatiga de las armaduras, normalmente, no es un factor relevante. Sin embargo, debido al empleo cada vez mayor de estructuras sujetas a cargas cíclicas y dimensionadas con base en el estado de ruptura (estado límite último), es importante que los efectos asociados a la fatiga sean analizados.

2.2. Durabilidad y vida útil a la fatiga

La norma (ACI 318, 2019) resalta que la durabilidad de las estructuras se refiere a la capacidad de resistir los procesos de degradación, preservando su integridad cuando es expuesta al ambiente para el cual fue proyectada. En ese contexto, la norma brasileña (ABNT NBR 15575, 2013) define vida útil de proyecto (VUP), como el intervalo de tiempo en el cual la estructura mantiene sus requisitos de durabilidad y desempeño, atendiendo los objetivos para los cuales fue propuesta. De acuerdo con (Branco y Paulo, 2012), una estructura alcanza su VUP cuando son detectadas manifestaciones patológicas (estéticas o estructurales) que perjudican su desempeño. Sin embargo, existen operaciones de mantenimiento que permiten restaurar la vida útil de las estructuras deterioradas.

Al contrario del término VUP, que aborda la vida útil de la estructura como un todo, la VUF es más restricta, y está asociada específicamente al intervalo de tiempo necesario para que las tensiones cíclicas promuevan y propaguen la fisuración en el elemento estructural. (Baroni, 2010) defiende que la VUF no culmina, necesariamente, con el colapso de la estructura, sino con fisuras en dimensiones críticas que pueden ser objeto indirecto de la falla. De esa forma, a lo largo de la VUP de puentes y viaductos, el tráfico de vehículos no debe promover variaciones excesivas de tensiones que provoquen el debilitamiento de la estructura frente a la fatiga.

3. MetodologÍa

3.1. Caracterización del puente sobre el Rio Chapecó

El ponte sobre el Rio Chapecó fue proyectado en 1987, con el objetivo de interconectar las ciudades de Xaxim y São Domingos, ambas en el estado de Santa Catarina - Brasil. El puente en estudio posee 170 m de extensión total (longitudinalmente), distribuidos en 3 vanos centrales de 33,60 m, 2 vanos de 28,00 m (uno para cada lado) y 2 vanos de 6,60 m, uno en cada extremo.

El tablero del puente posee un ancho total de 9,00 m, de los cuales 7,20 m son destinados a las fajas de rodamiento, y dos fajas de 0,90 m (una en cada borde) son destinadas a la circulación de peatones y ciclistas. La losa del tablero está apoyada sobre dos vigas longitudinales (30x170 cm), seis vigas transversales de sección 30x170 cm (una en cada apoyo), y diez vigas transversales de sección 30x170 cm (dos en cada vano - con excepción de los vanos en los extremos). El perfil transversal del vano central del puente es ilustrado en la Figura 1A. Para la confección de las vigas fue utilizado concreto con resistencia característica a la compresión de 20 MPa y acero CA-50 para las armaduras.

Figura 1. (A) Perfil transversal del puente sobre el Rio Chapecó; (B) Sección transversal, en centímetros, del trecho investigado de la Viga longitudinal (Adaptado del Departamento de Estradas e Rodagem de Santa Catarina, 1987).

Un análisis estructural preliminar del puente reveló que la condición más crítica frente a la fatiga se produce en el medio de los vanos centrales del puente. Siendo así, se optó por determinar la VUF de las vigas longitudinales presentes en esa sección (Figura 1B).

3.2. Determinación de los esfuerzos actuantes

El modelo estructural fue construido considerando las cargas permanentes y móviles, y los respectivos coeficientes de ponderación de las cargas verticales (CPV), conforme la (ABNT NBR 7188, 2013). La determinación de la línea de influencia y de la envolvente de solicitaciones fue realizada por medio del software Ftool (2018), que permite el análisis de estructuras en el plano.

Conforme recomienda la norma brasileña (ABNT NBR 6118, 2014), para la verificación a la fatiga, los esfuerzos solicitantes en el acero y concreto fueron determinados en régimen elástico, y el cálculo de las tensiones causadas por la flexión compuesta, en el Estado II - desconsiderando la resistencia a la tracción del concreto. Con relación a los momentos flectores, fue adoptada la combinación de acciones para el estado límite de servicio (ELS) a la fatiga, indicado por la respectiva norma.

Para la determinación del momento resistente y de los demás esfuerzos actuantes en la estructura fueron utilizadas las ecuaciones de equilibrio de fuerzas y las de (Pfeil, 1989), respectivamente. En cuanto al cálculo de las tensiones actuantes en las armaduras longitudinales y concreto, se adoptaron las ecuaciones (1) - (2), de (Süssekind, 1980), y Ecuación (3) de la (ABNT NBR 6118, 2014) para las armaduras transversales (α=90º).

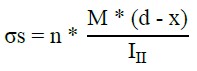(1)

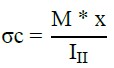(2)

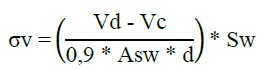(3)

Donde σs representa la tensión en las armaduras traccionadas (kN/cm²); n es la división entre el módulo de elasticidad del acero y del concreto; M es el momento de inercia (kN.cm); d es la distancia de la cara comprimida al centro de gravedad de las armaduras traccionadas (cm); x es la línea neutra (cm); I _II representa la inercia equivalente en el Estado II (cm⁴); 휎푐 es la tensión de compresión en el concreto (kN/cm²); 휎푣 es la tensión en las armaduras transversales (α=90º) (kN/cm²); Vd es el esfuerzo cortante de proyecto que actuará en los estribos (kN); Vc es el esfuerzo cortante absorbido por mecanismos complementares (concreto); y, Asw es el área de acero transversal necesaria a lo largo de 1 m (cm²/m).

Un análisis estructural reveló que el medio del mayor vano de la estructura presentaba el ponto de mayor variación de tensión para las armaduras sujetas a flexión y cizallamiento, y para el concreto sometido a compresión simple. Así, la verificación a la fatiga - según los criterios de la (ABNT NBR 6118, 2014) - fue realizada sobre esa sección (condición crítica). En cuanto a la variación de tensión, esa es la diferencia entre la máxima y la mínima tensión calculada, caso esos valores tengan signos contrarios, la diferencia será entre 0 (cero) y el mayor valor en módulo. En caso de puentes, esa variación de tensión será la relación entre los esfuerzos actuantes debido a las cargas permanentes con las ocasionadas por las cargas móviles y las cargas permanentes.

Además de eso, se creó el modelo de la estructura con los estados de cargas especificados en la (ABNT NBR 7188, 1984 y NB-2, 1961), a fin de comprobar que el puente fue proyectado conforme las normas vigentes en la época. Eso también permitió validar el método de cálculo de la resistencia de las armaduras por medio de las ecuaciones de equilibrio de fuerzas y el modelo representativo del puente.

3.3. Verificación de seguridad a la fatiga

La verificación de seguridad a la fatiga del puente fue realizada conforme las orientaciones de la (ABNT NBR 6118, 2014) por dos metodologías: limitación de tensiones y VUF. En cuanto a la primera metodología, deben ser consideradas la verificación por el estado límite último (ELU) a la fatiga (método de vida ilimitada) y el estado límite de servicio. En este trabajo, solo será realizada adoptándose la estructura en el ELU.

3.3.1 Limitación de tensiones

La verificación de seguridad a la fatiga por el método de limitación de tensiones fue realizada conforme las normas vigentes para evaluar la seguridad de la estructura frente a los daños causados por acciones cíclicas. La verificación de seguridad siguió las recomendaciones de la (ABNT NBR 6118, 2014), y fue realizada considerando la combinación frecuente de acciones, conforme la (ABNT NBR 8681, 2004). El cálculo de las cargas móviles fue realizado conforme el tren estándar brasileño de la (ABNT NBR 7188, 2013), posicionado en el punto más desfavorable de la estructura. Conforme recomienda la (ABNT NBR 6118, 2014), la verificación fue realizada en el concreto sujeto a compresión y en las armaduras sujetas a la flexión y cizallamiento. El análisis estructural no identificó esfuerzos de tracción en el punto estudiado, por tanto, la verificación de seguridad del concreto sujeto a tracción fue despreciada.

3.3.2 Vida útil a la fatiga

La verificación de la VUF del puente fue realizada para las armaduras sujetas a flexión, en el medio del mayor vano. Esta, tuvo como base la (ABNT NBR 6118, 2014), que presenta la curva S-N para las armaduras de estructuras de concreto armado. De acuerdo con (Bolotin, 1998), las curvas de fatiga fueron introducidas en 1860 por el alemán August Wӧhlner. La curva relaciona la magnitud de los ciclos de tensión y el número de ciclos necesarios para llevar el material a la ruptura.

Según la (ABNT NBR 6118, 2014), para utilizar un espectro real de cargas (o de la literatura), se debe considerar la regla de Palmgren-Miner, que relaciona el número N (número de ciclos para romper la estructura por fatiga, para cierta variación de tensión), con el número de ciclos experimentados (n). Así, el cálculo da VUF es dado por la Ecuación (4). De acuerdo con (ACI 215R-74, 1997; Nussbaumer et. al., 2011), los daños por fatiga deben ser acumulados de forma lineal, asumiendo el fin de la vida útil cuando la sumatoria sea igual a 1.

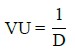(4)

Donde VU: representa la vida útil; y D: daño acumulado.

Para la frecuencia de paso de los vehículos, se adoptó la presentada por (Rossigali, 2013). Y, en cuanto al número de ciclos N (daño) del acero, este fue calculado de acuerdo con las Ecuaciones (5) - (6), propuestas por (Bolotin, 1998) y oriunda de curvas S-N como la presente en la (ABNT NBR 6118, 2014).

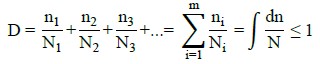(5)

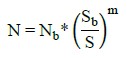(6)

Donde D: representa el daño acumulado; n _i : número de ciclos aplicados en el i-ésimo nivel de tensión; N _i :: vida en fatiga del i-ésimo nivel de tensión que corresponde al número de ciclos hasta la falla en ese nivel; N: número de ciclos asociados a la ruptura por fatiga; Nb: constante adimensional que viene de las curvas S-N, de la Norma (ABNT NBR 6118, 2014); Sb: constante con unidad de tensión; S: tensión en el material; y, m: exponente de la curva de fatiga.

Todos los valores de las cargas de cada vehículo fueron mayorados por los CPV de la (ABNT NBR 7188, 2013). Por consiguiente, se insertó de forma individual la carga para las respectivas tipologías del espectro del tráfico de la literatura, conjuntamente con el peso propio da estructura, determinándose los momentos flectores máximos y mínimos en el medio del mayor vano.

Conforme orientación de la (ABNT NBR 6118, 2014), se adoptó el índice de la relación del módulo de elasticidad del acero (Es) y del concreto (Ec) como 10; y se ignoró el daño causado por vehículos con cargas inferiores a 30 kN. En cuanto a la línea neutra (X _II ) y la inercia (I _II ) de la sección en el Estado II, y la distancia de la cara comprimida de la viga al centro de gravedad de las armaduras traccionadas (d), estos serán los mismos utilizados en la verificación a la fatiga por limitación de variación de tensión.

Dado que la determinación de la VUF fue realizada para las armaduras a flexión de la viga longitudinal, se utilizó la Ecuación 1 para la determinación de la tensión actuante en las mismas debido a las cargas de vehículos y peso propio.

En cuanto a la caracterización del espectro de vehículos, esa fue realizada con base en la literatura con el objetivo de determinar la carga actuante sobre la estructura y la VUF. Considerando la imposibilidad de realizar la medición del tráfico de vehículos actual, se utilizó la base de datos descrita por (Rossigali, 2013; Santos, 2013). Según los autores, el tráfico pesado de vehículos comerciales puede ser representado por 27 clases con diferentes dimensiones (longitudinal y transversal), diferentes distancias entre ejes, y diferentes cargas por eje. Un ejemplo de las características de una de las 27 clases estudiadas (2CC) es presentado en la Tabla 1. La caracterización de los vehículos pesados que trafican en el sistema de carreteras brasileño, descrita por (Rossigali, 2013; Santos, 2013), fue realizada en diferentes intervalos (1999 - 2011) y con el auxilio de diferentes administradoras de carreteras.

Tabla 1. Frecuencia relativa de la clase de vehículo 2CC, por faja de peso.

El tipo de vehículo (de acuerdo con la clase) y el número de vehículos (en cada clase) influye directamente en la intensidad de los momentos flectores, ciclo de tensiones y, consecuentemente, en el daño a la fatiga. El volumen de vehículos en cada clase fue determinado multiplicando el volumen medio diario por la frecuencia absoluta (en cada faja de peso, de cada clase).

De acuerdo con (Rossigali, 2013), carreteras con solamente una faja por sentido (como es el caso del puente en estudio) presentan un volumen medio diario de 6 mil vehículos por día. La frecuencia absoluta representa el número de observaciones de cada faja en relación al número total de observaciones. La frecuencia relativa es la relación entre el volumen de vehículos de una misma clase. El total de vehículos en cada clase es presentado en la Tabla 2.

Tabla 2. Volumen de vehículos para cada una de las 27 clases (considerando todas las fajas)
Clase	Volumen (vehíc.)	Clase	Volumen (vehíc.)	Clase	Volumen (vehíc.)	Clase	Volumen (vehíc.)
2CC	663,96	3C3	15,30	2I3	22,26	3T4	278,40
2C	745,32	3D4	9,60	3S1	10,14	3T6	51,18
3C	1026,96	2S1	268,92	3S2	44,52	3M6	10,02
4C	8,70	2S2	718,08	3S3	368,82	2CB	477,12
2C2	89,88	2S3	681,24	3I1	12,72	3CB	122,16
2C3	16,62	2I1	8,82	3I2	7,86	3BB	122,16
3C2	17,10	2I2	106,98	3I3	95,16	-	-
Total							6000

La posición de los vehículos también influye en el diagrama de tensiones. En ese trabajo, se adoptó la posición de los vehículos, del espectro de la literatura, en el centro de la faja conforme recomendaciones del (DNIT, 2005) y (Toledo, 2011). Para la construcción de la envolvente de esfuerzos, las cargas debido al tráfico fueron mayoradas por los CPV de la (ABNT NBR 7188, 2013).

4. Resultados y discusiÓn

4.1. Propiedades mecánicas de la viga longitudinal

El ancho eficaz de la capa superior, línea neutra e inercia de la viga longitudinal fueron determinados en el Estado II. con esos resultados, se calculó el momento resistente de la estructura para que pudiesen ser realizados refuerzos estructurales, caso fuese inferior al determinado con las cargas de la (ABNT NBR 7188, 2013). De este modo, dado que el ancho eficaz de la capa superior es igual a 401,60 cm, línea neutra de la sección en el estado último (x) igual a 10,35 cm, línea neutra de la sección en el Estado II (x₂) igual a 32,45 cm, se tiene que el momento de inercia (M_k) es igual a 6.512,37 kN.m y el momento resistente (I₂) igual a 4,05x10⁷cm⁴.

Considerando que el puente fue proyectado por la (ABNT NBR 7188, 1984) (norma vigente en la época do proyecto), se modeló la estructura considerando las cargas permanentes, el tren estándar brasileño de 300 kN, y el coeficiente de impacto (φ) de 1,23, especificado en la (ABNT NBR NB-2, 1961), conforme indicado por (Pfeil, 1979). El resultado es presentado en la Figura 2.

Figura 2. Envolvente de esfuerzos debido al tren estándar brasileño 300 y φ=1,23.

Se observa que el valor del momento flector en el medio del vano central es de 6.720,64 kN.m, por tanto, próximo del calculado por medio de las ecuaciones de equilibrio de fuerzas, con una diferencia de apenas 208,27 kN.m o aproximadamente 3,2 %. De esta forma, se comprueba que el puente fue proyectado conforme las normas vigentes en la época (1987), se valida la metodología de cálculo de la resistencia de las armaduras por medio de las ecuaciones de equilibrio de fuerzas y el modelo representativo de la estructura del puente.

4.2. Verificación a la fatiga

Los esfuerzos a la fatiga fueron determinados según las cargas de la (ABNT NBR 7188, 2013). Después de determinar las cargas permanentes y mayorar el tren estándar brasileño (TB-450 kN) y la carga de multitud por los respectivos coeficientes (CPV = 1,60), se obtuvieron los esfuerzos cortantes máximos y mínimos de 467,43 kN y -467,38 kN, y momentos flectores máximo (8.904,07 kN.m) y mínimo (1.083,10 kN.m), conforme ilustrado en las Figuras 3 e 4, en el medio del mayor vano del puente.

Figura 3.. Envolvente de esfuerzos cortantes con TB-450 y CPV de la (ABNT NBR 7188, 2013).

Figura 4. Envolvente de momento flector con TB-450 y CPV de la (ABNT NBR 7188, 2013).

Por tanto, se realizó la verificación a la fatiga del puente sobre el Rio Chapecó considerando las recomendaciones de la (ABNT NBR 6118, 2014) para las armaduras sujetas a flexión, concreto comprimido y para las armaduras de cizallamiento (estribos).

4.2.1 Armaduras a flexión

La sección de la viga longitudinal verificada posee 24 barras de acero con diámetro igual a 22,2 mm (Área de acero = 92,90 cm²). Para ese diámetro, la (ABNT NBR 6118, 2014) recomienda que la tensión en las armaduras sea limitada a ∆_fsd,fad = 180 MPa. Así, considerando las propiedades mecánicas del trecho de la viga longitudinal estudiada, se realizó la verificación a la fatiga de las armaduras a flexión en el medio del mayor vano del puente sobre el Rio Chapecó, considerando los esfuerzos del tren estándar brasileño 450 kN y los CPV de la (ABNT NBR 7188, 2013).

Las tensiones máximas y mínimas actuantes en las barras fue determinadas por la Ecuación 1. En el trecho investigado, la variación de la tensión (σs_max- σs_min) fue de 190,39 MPa, o sea, mayor que el límite (180 MPa) para barras de 22,2 mm. Por tanto, esa sección no es segura a la fatiga.

4.2.2 Concreto en compresión

La verificación a la fatiga del concreto en la sección más crítica fue realizada solo a compresión, pues este será el esfuerzo actuante en este punto. Así, la (ABNT NBR 6118, 2014) recomienda que esta tensión sea limitada a 45% de la resistencia de proyecto del concreto. Además de eso, la respectiva norma argumenta que las tensiones determinadas deberán ser obtenidas en un trecho no mayor que 30 cm de la cara comprimida. Así, dado que la línea neutra en el Estado II fue igual a 32,45 cm, se corrigieron las variaciones de tensiones por medio de semejanza de triángulos.

Para la determinación de la variación de tensión, ocasionada debido a los momentos máximo y mínimo en el medio del mayor vano de la estructura, se hizo uso de la Ecuación 2. La variación da tensión de compresión en el punto investigado fue igual a 3,56 MPa, menor que el límite normativo (6,43 MPa). Así, la sección del concreto sujeto a la compresión se encuentra segura a la fatiga.

Es importante resaltar que, de acuerdo con (Al-Khaiat y Fattuhi, 2001; Elaty, 2014), el concreto posee un aumento de resistencia a lo largo de los años. Ese aumento de resistencia depende de variables como relación agua/cemento, condiciones de exposición (temperatura, humedad) y régimen de curado. Aunque la mayor resistencia del concreto contribuye para reducir los daños asociados a la fatiga, esa consideración no puede ser incluida en el presente estudio debido a limitaciones administrativas. Así, optamos por hacer una verificación asumiendo la peor hipótesis funcional, o sea, manteniendo la resistencia del concreto constante.

4.2.3 Armaduras de cizallamiento

La sección de la viga longitudinal investigada posee estribos de acero ϕ10,0 mm (Área de acero = 4,62 cm²/m), espaciados a 17 cm. Para ese diámetro, la (ABNT NBR 6118, 2014) recomienda que la tensión sea limitada a ∆_fsd,fad =85 MPa. Conforme abordado por (Pfeil, 1979), la variación de tensión de cizallamiento en el medio del mayor vano del puente fue de 467,43 kN à -467,38 kN. Entretanto, se consideran las tensiones variando de 0 hasta el máximo valor (467,43 kN).

Para la determinación de la variación de tensión en las armaduras al cizallamiento, se adoptó la Ecuación 3, conforme la (ABNT NBR 6118, 2014). En cuanto a los esfuerzos, estos fueron corregidos para la combinación según el estado límite de servicio (ELS) a la fatiga.

La variación de tensión en las armaduras para esfuerzo cortante (estribos) en el trecho investigado fue de 122,26 MPa. Ese valor es superior a límite (85 MPa) para barras de ϕ10,0 mm, conforme (ABNT NBR 6118, 2014). Por tanto, la sección bajo cizallamiento no es segura a la fatiga.

4.3. Daño acumulado y vida útil a la fatiga

El cálculo del daño en la estructura debe considerar las tensiones debido al espectro real de vehículos y a la curva S-N de la (ABNT NBR 6118, 2014), descrita por la Ecuación 6. El valor límite de tensión fue calculado con base en las armaduras del tipo T1, que de acuerdo con la (ABNT NBR 6118, 2014) posee una curva S-N con coeficientes angulares de k₁= 5 e k₂= 9. El número límite de ciclos a la fatiga adoptado fue de N = 1x10⁶ ciclos. Ese número representa el punto de cambio en la inclinación de la curva S-N. El valor límite de la tensión calculada fue de 194,41 MPa.

Para valores de variación de tensión inferiores a 194,41 MPa, será considerado el trecho de la curva con inclinación igual a 9 y para variaciones arriba del valor límite de N = 1x10⁶, la inclinación igual a 5. Considerando la Ecuación 5 con N _b igual a 1x10⁶ ciclos, S _b igual a 194,41 MPa, exponente de la curva de fatiga (m) variando entre 5 e 9 y la tensión en el material (S) debido a cada faja de peso para cada clase de vehículo, se determinó el número de ciclos N a la fatiga.

Así, se adoptó el volumen de tráfico igual a 6.000 vehíc/día (2,19 millones/año), se calculó el daño en la estructura y el daño acumulado al año (D _ano ), por medio de la regla de Palmgren-Miner (Ecuación 5), o sea, sumatoria de la división entre el número de vehículos de la clase y faja de peso pasantes durante un año y el número de ciclos de fatiga debido a su carga.

La vida útil de la estructura es alcanzada cuando la sumatoria de los daños es igual a 1. Luego, al calcular la diferencia entre el valor unitario y el daño total en las armaduras a flexión a la fatiga durante un año, se tiene la vida útil de las mismas, en años. La Tabla 3 presenta el resultado del daño acumulado para cada clase de vehículo del espectro de (Rossigali, 2013), y la VUF, considerando los CPV de la (ABNT NBR 7188, 2013).

Tabla 3. Daño acumulado y vida útil a la fatiga del puente sobre el Rio Chapecó.

Por tanto, a vida útil del puente sobre el Rio Chapecó, considerando el tráfico de vehículos de Rossigali (2013) mayorados por los CPV de la (ABNT NBR 7188, 2013), es igual a 14,91 años, con un daño total acumulado de 6,71E-02 (unidad).

5. Consideraciones finales

Este estudio fue desarrollado con el objetivo de verificar si un puente proyectado en 1987, conforme las normas vigentes en la época (ABNT NBR NB-2, 1961; ABNT 7188, 1984) aún presenta seguridad a la fatiga según las normas vigentes actuales (ABNT NBR 7188, 2013; ABNT NBR 6118, 2014). Para esto, se estudió la situación más crítica de la estructura - la viga longitudinal en el medio del vano central. Con el desarrollo de la presente investigación fue posible concluir que:

• En la verificación a la fatiga de las armaduras longitudinales sujetas a flexión simple, considerando las cargas de la (ABNT NBR 7188, 2013), la tensión actuante fue de 190,39 MPa, o sea, superior al límite especificado por la norma, (180 MPa). Con relación a las armaduras transversales, la tensión actuante fue de, aproximadamente, 44 % superior al límite especificado en norma, también no atendiendo a los criterios de seguridad a la fatiga.
• En la verificación del concreto a la compresión, considerando las cargas de la (ABNT NBR 7188, 2013), se comprobó que el trecho investigado es seguro, con una tensión actuante de 3,56 MPa, abajo del límite de 6,43 MPa. De esa forma, se puede concluir que en caso que la fatiga ocurra en la estructura, ella ocurrirá inicialmente en los estribos, y no en el concreto;
• La VUF, debido al tráfico de vehículos reales del espectro de (Rossigali, 2013) y coeficientes mayoradores de las cargas dinámicas de la (ABNT NBR 7188, 2013), fue de 14,91 años. Esto, debido a que las cargas vigentes consideradas dieron como resultado tensiones mucho más altas que el límite a la fatiga de las armaduras a flexión;
• Después de los cálculos de verificación a la fatiga por el método de limitación de tensiones y por los daños acumulados, se concluye que las armaduras de flexión y los estribos del puente sobre el Rio Chapecó, no atendieron la verificación a la fatiga, solo el concreto a compresión, considerando las cargas de la (ABNT NBR 7188, 2013). En el caso del espectro de vehículos reales, las armaduras a flexión no atendieron a los criterios de seguridad de la regla de Palmgren-Miner (daños acumulados).

Es importante resaltar que aun cuando los análisis fueron realizados sobre un caso real, las características de las cargas (vehículos, tráfico) no representan, necesariamente, las condiciones reales de tráfico a que el puente está sujeto. De esa forma, la medición de las características de los vehículos y del tráfico in situ podría dar como resultado edades diferentes de VUF.

Además de eso, se recomienda que sea realizado un estudio minucioso de los elementos de la estructura para una verificación completa a la fatiga, visto que algunos de estos están sujetos a variaciones de tensión a lo largo de su extensión. Con eso, se podrá obtener una evaluación global del desempeño.

Referencias

Al-Khaiat, H., Fattuhi, N. (2001), Long-term strength development of concrete in arid conditions. Cement and Concrete Composites. 23(4-5)363-373. https://doi.org/10.1016/S0958-9465(01)00004-X

American Concrete Institute, ACI (1997), “ACI 215R-2: Considerations for Design of Concrete Structures Subjected to Fatigue Loading”. Michigan, Estados Unidos.

American Concrete Institute, ACI (2019). “ACI 318: Building Code Requirements for Structural Concrete”. Michigan, Estados Unidos.

Associação Brasileira de Normas Técnicas (1961). NB-2: Cálculo e Execução de Pontes de Concreto Armado. Rio de Janeiro.

Associação Brasileira de Normas Técnicas (1984). NBR 7188: Carga móvel em ponte rodoviária e passarela de pedestre. Rio de Janeiro.

Associação Brasileira de Normas Técnicas (2013). NBR 7188: Carga móvel em ponte rodoviária e passarela de pedestre. Rio de Janeiro.

Associação Brasileira de Normas Técnicas (2013). NBR 15575: Desempenho de edificações habitacionais. Rio de Janeiro.

Associação Brasileira de Normas Técnicas (2014). NBR 6118: Projeto de estruturas de concreto - Procedimento. Rio de Janeiro.

Baroni, H. J. M. (2010), “Simulação da vida útil de fadiga do concreto em vigas de tabuleiro de pontes em função do fluxo de veículos pesados”, Tese de Doutorado em Engenharia, Universidade Federal do Rio Grande do Sul, Porto Alegre.

cap. 1 Bolotin, V. V. (1998), Introduction. In: Bolotin V. V. “Mechanics of Fatigue”, Boca Raton, CRC Press LLC, , pp. 01-17.

Branco, F., Paulo, P. (2012), O projecto de pontes para vidas superiores a 100 anos. Revista ALCONPAT. 2(1):1-9. http://dx.doi.org/10.21041/ra.v2i1.20

Callister J., William D. (2008), “Ciência e engenharia de materiais: Uma introdução”. LTC, Rio de Janeiro, Brasil, p. 620. Tradução: Soares, S. M. S.

Cervo, T. C. (2004), “Estudo da resistência à fadiga de concretos de cimento Portland para pavimentação”, Tese de Doutorado em Engenharia, Universidade de São Paulo, São Paulo.

Confederação Nacional de Transporte, CNT (2018), “Pesquisa CNT de rodovias 2018: Relatório gerencial”. Brasília, Brasil.

Comité Euro-International du Betón, CEB (1988), “Fatigue of Concrete Structures. Bulletin d’Information Nº. 188”. Dubrovnik, Croácia.

Departamento de Estradas de Rodagem de Santa Catarina, DER (1987), “Projeto da Ponte sobre o Rio Chapecó na rodovia SC 451, entre os municípios de Xaxim e São Domingos”. Florianópolis, Brasil.

Departamento Nacional de Infraestrutura e Transporte, DNIT (2005), “Manual de Conservação Rodoviária”. Rio de Janeiro, Brasil.

Elaty, M. A. A. A. (2014), Compressive strength prediction of Portland cement concrete with age using a new model. HBRC Journal. 10(2)145-155. https://doi.org/10.1016/j.hbrcj.2013.09.005

Fan, Z., Sun, Y. (2019), Detecting and evaluation of fatigue damage in concrete with industrial computed tomography technology. Construction and Building Materials. 223:794-805. https://doi.org/10.1016/j.conbuildmat.2019.07.016

Fathalla, E., Tanaka, Y., Maekawa, K. (2018), Remaining fatigue life assessment of in-service road bridge decks based upon artificial neural networks. Engineering Structures. 171:602-616. https://doi.org/10.1016/j.engstruct.2018.05.122

Boletim Técnico da Escola Politécnica da USP, BT/PCC (2000), “Concreto com Fibras de Aço - Boletim Técnico PCC/260”. São Paulo, Brasil.

Access in 15 Mar. 2018 Ftool (2018), “A Graphical-Interactive Program for Teaching Structural Behavior”. Available in: <https://www.ftool.com.br/Ftool/>. .

Gao, Q., Dong, Z., Cui, K., Liu, C., Liu, Y. (2020), Fatigue performance of profiled steel sheeting-concrete bridge decks subjected to vehicular loads. Engineering Structures. 213:110558. https://doi.org/10.1016/j.engstruct.2020.110558

Hobbacher, A. F., Hicks, S. J., Karpenko, M., Franz, T., UY, B. (2016), Transfer of Australasian bridge design to fatigue verification system of Eurocode 3. Journal of Constructional Steel Research. 122:532-542. https://doi.org/10.1016/j.jcsr.2016.03.023

Meneghetti, L. C. (2007), “Análise do comportamento à fadiga de vigas de concreto armado reforçadas com PRF de vidro, carbono e aramida”, Tese de Doutorado em Engenharia, Universidade Federal do Rio Grande do Sul, Porto Alegre.

Nussbaumer, A., Borges, L., Davaine, L. (2011), “Fatigue design of steel and composite structures”. Wiley, Hoboken, Estados Unidos, p. 167.

Pfeil, W. (1979), “Pontes em concreto armado: Elementos de projeto, solicitações, dimensionamento”. LTC, Rio de Janeiro, Brasil, p. 433.

Pfeil, W. (1989), “Concreto armado”. LTC, Rio de Janeiro, Brasil, p. 812.

Rossigali, C. E. (2013), “Atualização do modelo de cargas móveis para pontes rodoviárias de pequenos vãos no Brasil”, Tese de Doutorado em Engenharia Civil, Universidade Federal do Rio de Janeiro, Rio de Janeiro.

Santos, L. A., Pfeil, M. S. (2014), Desenvolvimento de modelo de cargas móveis para verificação de fadiga em pontes rodoviárias. Engenharia Estudo e Pesquisa ABPE 14(1):40-47.

Santos, L. F. (2013), “Desenvolvimento de um modelo de cargas móveis para verificação de fadiga em pontes rodoviárias”, Trabalho de Conclusão de Curso em Engenharia Civil, Universidade Federal do Rio de Janeiro, Rio de Janeiro.

Silva, C. J. G., Monteiro, E. C. B., Vitório, J. P. A. (2018), Condições estruturais e funcionais de pontes e viadutos das rodovias federais de Pernambuco. Revista ALCONPAT. 8(1)79-93. http://dx.doi.org/10.21041/ra.v8i1.199

Süssekind, J. C. (1980), “Curso de Concreto: Concreto Armado - Volume I”. Globo, Porto Alegre, Brasil, p. 376.

Toledo, R. L. S. (2011), “Avaliação de vida útil à fadiga em ponte mista aço-concreto considerando o espectro de veículos reais”, Trabalho de Conclusão de Curso em Engenharia, Universidade Federal do Rio de Janeiro, Rio de Janeiro.

Yadav, I. N., Thapa, K. B. (2020), Fatigue damage model of concrete materials. Theoretical and Applied Fracture Mechanics. 108:102578. https://doi.org/10.1016/j.tafmec.2020.102578