Pesquisa Aplicada

https://doi.org/10.21041/ra.v11i2.515

Verificação de Segurança à fadiga de pontes em concreto armado conforme ABNT NBR 6118, 2014.

Safety verification of fatigue of a reinforced concrete bridge according to ABNT NBR 6118 2014

Verificación de seguridad de la fatiga de puentes en hormigón armado según ABNT NBR 6118:2014

M. D. Rossato^{1 *}, G. S. Munhoz² , R. B. P. dos Santos¹, L. M. O. Scoz¹

¹ Departamento de Engenharia Civil, Escola do Mar, Ciência e Tecnologia, Universidade do Vale do Itajaí - UNIVALI, Itajaí, Brasil..

² Departamento de Construção Civil, Universidade Federal do Paraná - UFPR, Curitiba, Brasil..

^* Autor de contato: mateusrossato.engcivil@gmail.com

Recepção: 16 de setembro de 2020.
Aceitação: 20 de janeiro de 2021.
Publicação: 01 de maio de 2021

Citar como: Rossato, M. D., Munhoz, G. S., P. dos Santos, R. B., Scoz, L. M. (2021), "Verificação de Segurança à fadiga de pontes em concreto armado conforme ABNT NBR 6118, 2014.", Revista ALCONPAT, 11 (2), pp. 109 – 123, DOI: https://doi.org/10.21041/ra.v11i2.515

Resumo
Nesse estudo de caso, a segurança à fadiga de uma ponte projetada em 1987 foi verificada segundo a norma vigente brasileira. Elaborou-se um modelo estrutural para determinar e verificar a seção mais crítica considerando o trem-tipo e o espectro de veículos da literatura. Segundo o método de limitação de variação de tensões, conclui-se que o concreto sujeito à compressão atende aos critérios, mas a área de aço não é suficiente para combater os esforços cortante e de flexão. Pela regra de Palmgren Miner, a vida útil à fadiga nas armaduras sujeitas à flexão é de 14,91 anos. Uma análise mais detalhada da estrutura e do espectro de veículos é necessária para reiterar tais resultados.
Palavras-chave: fadiga, ponte, regra de Palmgren-Miner, vida útil.

Abstract
In this case study, the fatigue security of a bridge designed in 1987 was examined considering the current Brazilian standard. A structural model was developed to determine and verify fatigue security in the most critical section considering the Brazilian Load Model and the literature’s vehicle spectrum. According to the stress variation method, it concludes that the concrete submitted to compression meets the minimum criteria, but the steel section is not enough to resist shearing and flexural stresses. Pursuant to the Palmgren-Miner rule, the fatigue service life of the reinforcement’s bars under flexural stress is 14,91 years. A more detailed structural analysis of the bridge and the vehicle spectrum is necessary to confirm these results.
Keywords: fatigue, bridge, Palmgren-Miner rule, service life.

Resumen
En este estudio, se verificó la seguridad a la fatiga de un puente proyectado en 1987 según la normativa brasileña vigente. Se construyó un modelo estructural para determinar y verificar la sección más crítica considerando el modelo estándar brasileño y el espectro de vehículos en la literatura. Según el método de variación de esfuerzos, se concluye que el hormigón sometido a compresión cumple con los criterios, pero la sección de acero no es suficiente para resistir los esfuerzos cortantes y de flexión. Por la regla de Palmgren-Miner, la vida útil a la fatiga de las armaduras sometidas a flexión es de 13,91 años. Es necesario un análisis más detallado de la estructura y del espectro de carga para confirmar estos resultados.
Palabras clave: fatiga, puente, regla de Palmgren-Miner, vida útil.

1. IntroduÇÃo

No Brasil, o transporte de bens e pessoas acontece, majoritariamente, por meio de uma vasta malha rodoviária, com aproximadamente 1,7 milhão de quilômetros de extensão. A movimentação de cargas nesse modal corresponde a 61% da matriz nacional de transportes (CNT, 2018). Nesse contexto, (Baroni, 2010) defende que as obras de arte especiais (OAEs) - pontes e viadutos - são elementos fundamentais do sistema de transportes, e assegurar sua funcionalidade, segurança e durabilidade é de suma importância.

Nas últimas décadas, a falta de políticas de manutenção e reparo das OAEs no Brasil têm contribuído para acelerar o processo de desgaste e deterioração dessas estruturas. Grande parte das pontes brasileiras foi construída entre os anos 50 e 70 e, portanto, projetadas por normas que não previam os carregamentos, nem a intensidade de tráfego existentes atualmente (Silva et.al., 2018).

Os principais danos que comprometem o desempenho das OAEs estão relacionados à corrosão, ao impacto físico e à erosão de fundações. Entretanto, (Fathalla et.al., 2018) apontam que a vida útil de pontes e viadutos também está diretamente associada às variações cíclicas de tensão devido ao tráfego de veículos. (Hobbacher et.al., 2016) aponta que após um determinado número de ciclos de carga-descarga, tem-se a formação e a propagação de fissuras que podem levar ao colapso da estrutura por fadiga. (Gao et.al., 2020) estudaram a vida útil à fadiga (VUF) de pontes com estruturas mistas aço-concreto e observaram que, nesse caso, a resistência do concreto teve pouco impacto na determinação da VUF. Isso foi reiterado por (Santos, 2013), que provou que o colapso por fadiga pode acontecer com tensões inferiores ao limite elástico do conjunto aço-concreto.

A norma brasileira (ABNT NBR 6118, 2014) é utilizada para avaliar os danos em estruturas de concreto devido às ações cíclicas. Essa norma determina os critérios que devem ser adotados para a verificação do estado limite último à fadiga (método de vida ilimitada) e do estado limite de serviço. Nesse caso, a verificação à fadiga por meio da limitação de tensões é preferencialmente recomendada, fazendo o uso dos carregamentos presentes na (ABNT NBR 7188, 2013).

O carregamento proposto pela norma brasileira (ABNT NBR 7188, 2013), que aborda as cargas móveis para pontes rodoviárias e substituiu a (ABNT NBR 7188, 1984), não apresenta configurações sobre o tráfego de veículos reais, mas um carregamento hipotético, denominado trem-tipo. Além disso, é prevista uma carga uniformemente distribuída por unidade de área, visando representar a passagem de veículos leves ou multidão. Excepcionalmente, caso o espectro de cargas esteja disponível, pode-se utilizar a regra de Palmgren-Miner, que também permite determinar a vida útil da estrutura à fadiga. Segundo esse método, supõe-se que os danos à fadiga se acumulam linearmente com o número de ciclos sendo esses danos denominados, conforme (Fan e Sun, 2019), como o processo de deterioração que culmina com a redução da área resistente da seção transversal.

Esse estudo foi desenvolvido com o objetivo de verificar a segurança à fadiga de uma ponte projetada em 1987 conforme a (ABNT NBR 6118, 2014). Foram utilizados dois métodos, limitação de variação de tensões e vida útil à fadiga. Para tal, estudou-se a situação mais crítica da estrutura - a viga longarina no meio do vão central.

2. ContextualizaÇÃo

2.1. O mecanismo da fadiga na deterioração de pontes

De acordo com (Yadav e Thapa, 2020), a fadiga é um mecanismo de falha estrutural que ocorre em um material submetido a variações de tensões repetitivas, ou seja, que oscilam de forma intermitente durante um determinado intervalo de tempo. O conjunto das etapas de carga e descarga é denominado ciclo. Vários ciclos culminam com o surgimento de microfissuras ou com a propagação de microfissuras pré-existentes, podendo causar o colapso da estrutura (Cervo, 2004). Quanto maior for a magnitude dos carregamentos intermitentes, menor será o número de ciclos necessários para romper a estrutura (BT/PCC, 2000).

As pontes e os viadutos são estruturas sujeitas ao fenômeno de fadiga pela acumulação de danos decorrentes da atuação de ciclos não uniformes de variação de tensão ocasionados pela passagem de veículos com diferentes características. A verificação desse fenômeno em estruturas de obras de arte especiais, principalmente em situações de tráfego intermitente, é essencial para garantir a segurança estrutural (Santos e Pfeil, 2014).

(Callister e William, 2008) afirmam que a ruptura por fadiga é de natureza frágil, ou seja, existe pouca (ou nenhuma) deformação plástica generalizada. De modo geral, o colapso ocorre com a propagação de fissuras, e com a superfície de fratura perpendicular à direção de aplicação da tensão. Contudo, no âmbito do concreto, o (Comité Euro-International du Béton, 1988) defende que não existe colapso exclusivamente por fadiga. Nesse caso, a ruptura das estruturas de concreto acontece devido à deterioração progressiva das fissuras causadas pelo carregamento cíclico.

Considerando as estruturas em concreto armado, (Meneghetti, 2007) comprovou que a fadiga das armaduras, normalmente, não é um fator relevante. Contudo, devido ao emprego cada vez maior de estruturas sujeitas a carregamentos cíclicos e dimensionadas com base no estado de ruptura (estado limite último), é importante que os efeitos associados à fadiga sejam analisados.

2.2. Durabilidade e vida útil à fadiga

A norma (ACI 318, 2019) ressalta que a durabilidade das estruturas diz respeito à capacidade em resistir aos processos de degradação, preservando sua integridade quando exposta ao ambiente para o qual foi projetada. Nesse contexto, a norma brasileira (ABNT NBR 15575, 2013) define vida útil de projeto (VUP), como o intervalo de tempo no qual a estrutura mantém os seus requisitos de durabilidade e desempenho, atendendo aos objetivos para o qual foi proposta.

De acordo com (Branco e Paulo, 2012), uma estrutura atinge sua VUP quando são detectadas manifestações patológicas (estéticas ou estruturais) que prejudicam o seu desempenho. No entanto, há operações de manutenção que permitem restaurar a vida útil das estruturas deterioradas.

Ao contrário do termo VUP, que aborda a vida útil da estrutura como um todo, a VUF é mais restrita, e está associado especificamente ao intervalo de tempo necessário para as tensões cíclicas promoverem e propagarem a fissuração no elemento estrutural. (Baroni, 2010) defende que a VUF não culmina, necessariamente, com o colapso da estrutura, mas com fissuras em dimensões críticas que podem ser objeto indireto da falha. Dessa forma, ao longo da VUP de pontes e viadutos, o tráfego de veículos não deve promover variações excessivas de tensões que provoquem o enfraquecimento da estrutura perante à fadiga.

3. Metodologia

3.1. Caracterização da ponte sobre o Rio Chapecó

A ponte sobre o Rio Chapecó foi projetada em 1987, com o objetivo de interligar as cidades de Xaxim e São Domingos, ambas no estado de Santa Catarina - Brasil. A ponte sob estudo possui 170 m de extensão total (longitudinalmente), distribuídos em 3 vãos centrais de 33,60 m, 2 vãos de 28,00 m (um para cada lado) e 2 vãos de 6,60 m, um em cada extremidade.

O tabuleiro da ponte possui uma largura total de 9,00 m, dos quais 7,20 m são destinados às faixas de rolamento, e duas faixas de 0,90 m (uma em cada bordo) são destinadas à circulação de pedestres e ciclistas. A laje do tabuleiro é apoiada sobre duas vigas longarinas (30x170 cm), seis vigas transversinas de seção 30x170 cm (uma em cada apoio), e dez vigas transversinas de seção 30x170 cm (duas em cada vão - com exceção dos vãos de extremidade). O perfil transversal do vão central da ponte é ilustrado na Figura 1A. Para a confecção das vigas foi utilizado concreto com resistência característica à compressão de 20 MPa e aço CA-50 para as armaduras.

Figura 1. (A) Perfil transversal da ponte sobre o Rio Chapecó; (B) Seção transversal, em centímetros, do trecho investigado da longarina (Adaptado do Departamento de Estradas de Rodagem de Santa Catarina, 1987).

Uma análise estrutural preliminar da ponte revelou que a condição mais crítica frente à fadiga acontece no meio dos vãos centrais da ponte. Sendo assim, optou-se por determinar a VUF das longarinas presentes nessa seção (Figura 1B).

3.2. Determinação dos esforços atuantes

O modelo estrutural foi construído considerando as cargas permanentes e móveis, e os respectivos coeficientes de ponderação das cargas verticais (CPV), conforme a (ABNT NBR 7188, 2013). A determinação da linha de influência e da envoltória de solicitações foi feita por meio do software Ftool (2018), que permite a análise de estruturas no plano.

Conforme recomenda a norma brasileira (ABNT NBR 6118, 2014), para a verificação à fadiga, os esforços solicitantes no aço e concreto foram determinados no regime elástico, e o cálculo das tensões decorrentes da flexão composta, no Estádio II - desconsiderando a resistência à tração do concreto. Em relação aos momentos fletores, foi adotada a combinação de ações para o estado limite de serviço (ELS) à fadiga, indicado pela respectiva norma.

Para a determinação do momento resistente e dos demais esforços atuantes na estrutura foram utilizados as equações de equilíbrio de forças e as de (Pfeil, 1989), respectivamente. Quanto ao cálculo das tensões atuantes nas armaduras longitudinais e concreto, adotou-se as equações (1) - (2), de (Süssekind, 1980), e Equação (3) da (ABNT NBR 6118, 2014) para as armaduras transversais (α=90º).

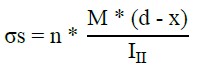(1)

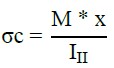(2)

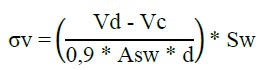(3)

Onde σs representa a tensão nas armaduras tracionadas (kN/cm²); n é a divisão entre o módulo de elasticidade do aço e do concreto; M é o momento de inércia (kN.cm); d é a distância da face comprimida ao centro de gravidade das armaduras tracionadas (cm); x é a linha neutra (cm); I_II representa a inércia equivalente no Estádio II (cm⁴); "σc" é a tensão de compressão no concreto (kN/cm²); σv é a tensão nas armaduras transversais (α=90º) (kN/cm²); Vd é o esforço cortante de projeto que atuará nos estribos (kN); Vc é o esforço cortante absorvido por mecanismos complementares (concreto); e, Asw é a área de aço transversal necessária ao longo de 1 m (cm²/m).

Uma análise estrutural revelou que o meio do maior vão da estrutura apresentava o ponto de maior variação de tensão para as armaduras sujeitas à flexão e cisalhamento, e para o concreto submetido à compressão simples. Assim, a verificação à fadiga - segundo os critérios da (ABNT NBR 6118, 2014) - foi feita sobre essa seção (condição crítica). Quanto à variação de tensão, essa é a diferença entre a máxima e a mínima tensão calculada, caso esses valores tenham sinais contrários, a diferença será entre 0 (zero) e o maior valor em módulo. No caso de pontes, essa variação de tensão será a relação entre os esforços atuantes devido às cargas permanentes com as ocasionadas pelas cargas móveis mais as cargas permanentes.

Além disso, criou-se o modelo da estrutura com os carregamentos especificados na (ABNT NBR 7188, 1984 e NB-2, 1961), a fim de comprovar que a ponte foi projetada conforme as normas vigentes na época. Isso também permitiu validar o método de cálculo da resistência das armaduras por meio das equações de equilíbrio de forças e o modelo representativo da ponte.

3.3. Verificação de segurança à fadiga

A verificação de segurança à fadiga da ponte foi feita conforme as orientações da (ABNT NBR 6118, 2014) por duas metodologias: limitação de tensões e vida útil à fadiga. Quanto à primeira metodologia, devem ser considerados a verificação pelo estado limite último (ELU) à fadiga (método de vida ilimitada) e estado limite de serviço. Neste trabalho, apenas será realizado adotando-se a estrutura no ELU.

3.3.1 Limitação de tensões

A verificação de segurança à fadiga pelo método de limitação de tensões foi feita conforme as normas vigentes para avaliar a seguridade da estrutura frente aos danos causados por ações cíclicas. A verificação de segurança seguiu as recomendações da (ABNT NBR 6118, 2014), e foi feita considerando a combinação frequente de ações, conforme a (ABNT NBR 8681, 2004). O cálculo das cargas móveis foi feito conforme o trem-tipo da (ABNT NBR 7188, 2013), posicionado no ponto mais desfavorável da estrutura.

Conforme recomenda a (ABNT NBR 6118, 2014), a verificação foi realizada no concreto sujeito à compressão e nas armaduras sujeitas à flexão e cisalhamento. A análise estrutural não identificou esforços de tração no ponto estudado, portanto, a verificação de segurança do concreto sujeito à tração foi desprezada.

3.3.2 Vida útil à fadiga

A verificação da VUF da ponte foi realizada para as armaduras sujeitas à flexão, no meio do maior vão. Esta, teve como base as orientações da (ABNT NBR 6118, 2014), que apresenta a curva S-N para as armaduras de estruturas em concreto armado. De acordo com (Bolotin, 1998), as curvas de fadiga foram introduzidas em 1860 pelo alemão August Wӧhlner. A curva relaciona a magnitude dos ciclos de tensão e o número de ciclos necessários para levar o material à ruptura.

Segundo a (ABNT NBR 6118, 2014), para utilizar um espectro real de cargas (ou da literatura), deve-se considerar a regra de Palmgren-Miner, que relaciona o número N (número de ciclos para romper a estrutura por fadiga, para certa variação de tensão), com o número de ciclos experimentados (n). Assim, o cálculo da VUF é dado pela Equação (4). De acordo com (ACI 215R-74, 1997; Nussbaumer et. al., 2011), os danos à fadiga devem ser acumulados de forma linear, assumindo o fim da vida útil quando o somatório for igual a 1.

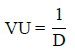(4)

Onde VU representa a vida útil; e D, o dano acumulado.

Para a frequência de passagem dos veículos, adotou-se a apresentada por (Rossigali, 2013). E, quanto ao número de ciclos N (dano) do aço, este foi calculado de acordo com as Equações (5) - (6), proposta por (Bolotin, 1998) e oriunda de curvas S-N como a presente na (ABNT NBR 6118, 2014).

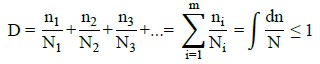(5)

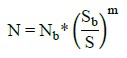(6)

Onde D representa o dano acumulado; n _i é o número de ciclos aplicados no i-ésimo nível de tensão; N _i : é a vida em fadiga do i-ésimo nível de tensão que corresponde ao número de ciclos até a falha nesse nível; N é o número de ciclos associados à ruptura por fadiga; Nb é uma constante adimensional que advém das curvas S-N, da Norma (ABNT NBR 6118, 2014); Sb é uma constante com unidade de tensão; S é a tensão no material; e, m é o expoente da curva de fadiga.

Todos os valores das cargas de cada veículo foram majorados pelos CPV da (ABNT NBR 7188, 2013). Por conseguinte, inseriu-se de forma individual o carregamento para as respectivas tipologias do espectro do tráfego da literatura, juntamente com o peso próprio da estrutura, determinando-se os momentos fletores máximos e mínimos no meio do maior vão.

Conforme orientação da (ABNT NBR 6118, 2014), adotou-se o índice da relação do módulo de elasticidade do aço (Es) e do concreto (Ec) como 10; e ignorou-se o dano causado por veículos com cargas inferiores a 30 kN. Quanto à linha neutra (X _II ) e a inércia (I _II ) da seção no Estádio II, e a distância da face comprimida da viga ao centro de gravidade das armaduras tracionadas (d), estes serão os mesmos utilizados na verificação à fadiga por limitação de variação de tensão.

Dado que a determinação da VUF foi realizada para as armaduras à flexão da longarina, utilizou-se da Equação 1 para a determinação da tensão atuante nas mesmas devido aos carregamentos de veículos e peso próprio.

Quanto à caracterização do espectro de veículos, essa foi realizada com base na literatura com o objetivo de determinar o carregamento atuante sobre a estrutura e a VUF. Considerando a impossibilidade de realizar a medição do tráfego de veículos atual, utilizou-se a base de dados descrita por (Rossigali, 2013; Santos, 2013). Segundo os autores, o tráfego pesado de veículos comerciais pode ser representado por 27 classes com diferentes dimensões (longitudinal e transversal), diferentes distâncias entre eixos, e diferentes cargas por eixo. Um exemplo das características de uma das 27 classes estudadas (2CC) é apresentado na Tabela 1. A caracterização dos veículos pesados que trafegam no sistema rodoviário brasileiro, descrita por (Rossigali, 2013; Santos, 2013), foi feita em diferentes intervalos (1999 - 2011) e com o auxílio de diferentes administradoras de rodovias.

Tabela 1. Frequência relativa da classe de veículo 2CC, por faixa de peso.

O tipo de veículo (de acordo com a classe) e o número de veículos (em cada classe) influencia diretamente na intensidade dos momentos fletores, ciclo de tensões e, consequentemente, no dano à fadiga. O volume de veículos em cada classe foi determinado multiplicando o volume médio diário pela frequência absoluta (em cada faixa de peso, de cada classe).

De acordo com (Rossigali, 2013), rodovias com apenas uma faixa por sentido (como é o caso da ponte sob estudo) apresentam um volume médio diário de 6 mil veículos por dia. A frequência absoluta representa o número de observações de cada faixa em relação ao número total de observações. A frequência relativa é a relação entre o volume de veículos de uma mesma classe. O total de veículos em cada classe é apresentado na Tabela 2.

Tabela 2. Volume de veículos para cada uma das 27 classes (considerando todas as faixas).
Classe	Volume (veículos)	Classe	Volume (veículos)	Classe	Volume (veículos)	Classe	Volume (veículos)
2CC	663,96	3C3	15,30	2I3	22,26	3T4	278,40
2C	745,32	3D4	9,60	3S1	10,14	3T6	51,18
3C	1026,96	2S1	268,92	3S2	44,52	3M6	10,02
4C	8,70	2S2	718,08	3S3	368,82	2CB	477,12
2C2	89,88	2S3	681,24	3I1	12,72	3CB	122,16
2C3	16,62	2I1	8,82	3I2	7,86	3BB	122,16
3C2	17,10	2I2	106,98	3I3	95,16	-	-
Total							6000

A posição dos veículos também influencia no diagrama de tensões. Nesse trabalho, adotou-se a posição dos veículos, do espectro da literatura, no centro da faixa conforme recomendações do (Departamento Nacional de Infraestrutura e Transporte, 2005) e (Toledo, 2011). Para a construção da envoltória de esforços, as cargas devido ao tráfego foram majoradas pelos coeficientes de ponderação das cargas verticais da (ABNT NBR 7188, 2013).

4. Resultados e discussÃo

4.1. Propriedades mecânicas da longarina

A largura colaborante da mesa superior, linha neutra e inércia da longarina foram determinadas no Estádio II. Com esses resultados, calculou-se o momento resistente da estrutura para que pudesse ser realizados reforços estruturais, caso ele fosse inferior ao determinado com os carregamentos da (ABNT NBR 7188, 2013).

Deste modo, dado que a largura colaborante da mesa superior é igual a 401,60 cm, linha neutra da seção no estado último (x) igual a 10,35 cm, linha neutra da seção no Estádio II (x₂) igual a 32,45 cm, tem-se que o momento de inércia (M_k) é igual a 6.512,37 kN.m e o momento resistente (I₂) igual a 4,05x10⁷cm⁴.

Considerando que a ponte foi projetada sob a (ABNT NBR 7188, 1984) (norma vigente à época do projeto), modelou-se a estrutura considerando os carregamentos permanentes, o trem-tipo de 300 kN, e o coeficiente de impacto (φ) de 1,23, especificado na (ABNT NBR NB-2, 1961), conforme indicado por (Pfeil, 1979). O resultado é apresentado na Figura 3.

Figura 3. Envoltória de esforços devido ao trem-tipo 300 e φ=1,23.

Observa-se que o valor do momento fletor no meio do vão central é de 6.720,64 kN.m, portanto, próximo do calculado por meio das equações de equilíbrio de forças, com uma diferença de apenas 208,27 kN.m ou aproximadamente 3,2 %. Desta forma, atesta-se que a ponte foi projetada conforme as normas vigentes na época (1987), valida-se a metodologia do cálculo da resistência das armaduras por meio das equações de equilíbrio de forças e o modelo representativo da estrutura da ponte.

4.2. Verificação à fadiga

Os esforços à fadiga foram determinados segundo os carregamentos da (ABNT NBR 7188, 2013). Após determinar as cargas permanentes e majorar o trem-tipo (TB-450 kN) e a carga de multidão pelos respectivos coeficientes (CPV = 1,60), obteve-se esforços cortantes máximos e mínimos de 467,43 kN e -467,38 kN, e momentos fletores máximo (8.904,07 kN.m) e mínimo (1.083,10 kN.m), conforme ilustrado nas Figuras 4 e 5, no meio do maior vão da ponte.

Figura 4. Envoltória de esforços cortante com TB-450 e CPV da (ABNT NBR 7188, 2013).

Figura 5. Envoltória de momento fletor com TB-450 e CPV da (ABNT NBR 7188, 2013).

Portanto, realizou-se a verificação à fadiga da ponte sobre o Rio Chapecó considerando as recomendações da (ABNT NBR 6118, 2014) para as armaduras sujeitas à flexão, concreto comprimido e para as armaduras de cisalhamento (estribos).

4.2.1 Armaduras à flexão

A seção da longarina verificada possui 24 barras de aço com diâmetro igual a 22,2 mm (Área de aço = 92,90 cm²). Para esse diâmetro, a (ABNT NBR 6118, 2014) recomenda que a tensão nas armaduras seja limitada a ∆_fsd,fad = 180 MPa. Assim, considerando as propriedades mecânicas do trecho da longarina estudada, realizou-se a verificação à fadiga das armaduras à flexão no meio do maior vão da ponte sobre o Rio Chapecó, considerando os esforços do trem-tipo 450 kN e os coeficientes de ponderação das cargas verticais da (ABNT NBR 7188, 2013).

Para a determinação das tensões máximas e mínimas atuantes nas barras adotou-se a Equação 1. No trecho investigado, a variação da tensão (σs_max - σs_min) foi de 190,39 MPa, ou seja, maior que o limite (180 MPa) para barras de 22,2 mm. Portanto, essa seção não é segura à fadiga.

4.2.2 Concreto à compressão

A verificação à fadiga do concreto no meio do vão da ponte foi realizada apenas à compressão, pois este será o esforço atuante neste ponto. Assim, a (ABNT NBR 6118, 2014) recomenda que esta tensão seja limitada a 45% da resistência de projeto do concreto. Além disso, a respectiva norma argumenta que as tensões determinadas deverão ser obtidas em um trecho não maior que 30 cm da face comprimida. Assim, dado que a linha neutra no Estádio II foi igual a 32,45 cm, corrigiu-se as variações de tensões por meio de semelhança de triângulos.

Para a determinação da variação de tensão, ocasionada devido aos momentos máximo e mínimo no meio do maior vão da estrutura, fez-se uso da Equação 2. A variação da tensão de compressão no ponto investigado foi igual a 3,56 MPa, menor do que o limite normativo (6,43 MPa). Deste modo, a seção do concreto sujeito à compressão encontra-se segura à fadiga.

É importante salientar que, de acordo com (Al-Khaiat e Fattuhi, 2001; Elaty, 2014), o concreto possui um ganho de resistência ao longo dos anos. Esse ganho de resistência depende de variáveis como relação água/cimento, condições de exposição (temperatura, umidade) e regime de cura. Apesar de uma maior resistência do concreto contribuir para reduzir os danos associados à fadiga, essa consideração não pôde ser incluída no presente estudo devido a limitações administrativas. Assim, optamos por fazer uma verificação assumindo a pior hipótese funcional, ou seja, mantendo a resistência do concreto constante.

4.2.3 Armaduras de cisalhamento

A seção da longarina sob investigação possui estribos de aço ϕ10,0 mm (Área de aço = 4,62 cm²/m), espaçados em 17 cm. Para esse diâmetro, a (ABNT NBR 6118, 2014) recomenda que a tensão seja limitada a ∆_fsd,fad = 85 MPa. Conforme abordado por (Pfeil, 1979), a variação de tensão de cisalhamento no meio do maior vão da ponte foi de 467,43 kN à -467,38 kN. Entretanto, considera-se as tensões variando de 0 (zero) até o máximo valor, neste caso 467,43 kN.

Para a determinação da variação de tensão nas armaduras ao cisalhamento, adotou-se a Equação 3, conforme a (ABNT NBR 6118, 2014). Quanto aos esforços, estes foram corrigidos para a combinação segundo o estado limite de serviço (ELS) à fadiga.

A variação de tensão nas armaduras para o esforço cortante (estribos) no trecho investigado da ponte foi de 122,26 MPa. Esse valor é superior ao limite (85 MPa) para barras de ϕ10,0 mm, conforme (ABNT NBR 6118, 2014). Portanto, a seção sob cisalhamento não é segura à fadiga.

4.3. Dano acumulado e vida útil à fadiga

O cálculo do dano na estrutura deve considerar as tensões devido ao espectro real de veículos e à curva S-N (Curva de Wöeller), da (ABNT NBR 6118, 2014), conforme descrita pela Equação 6. O valor limite de tensão foi calculado com base nas armaduras do tipo T1, que de acordo com a (ABNT NBR 6118, 2014) possui uma curva S-N com coeficientes angulares de k₁= 5 e k₂ = 9. O número limite de ciclos à fadiga adotado foi de N = 1x10⁶ ciclos. Esse número representa o ponto de mudança na inclinação da curva S-N. O valor limite da tensão calculada foi de 194,41 MPa.

Para valores de variação de tensão inferiores a 194,41 MPa, será considerado o trecho da curva com inclinação igual a 9. Para variações acima do valor limite de N = 1x10⁶, adotar-se-á inclinação igual a 5. Considerando a Equação 5 com N _b igual a 1x10⁶ ciclos, S _b igual a 194,41 MPa, expoente da curva de fadiga (m) variando entre 5 e 9 e a tensão no material (S) devido à cada faixa de peso para cada classe de veículo, determinou-se o número de ciclos N à fadiga.

Em seguida, adotando-se o volume de tráfego igual a 6.000 veic/dia (2,19 milhões/ano), calculou-se o dano na estrutura e o acúmulo de dano ao ano (D_ano), por meio da regra de Palmgren-Miner (Equação 5), ou seja, somatório da divisão entre o número de veículos da classe e faixa de peso passantes durante um ano e o número de ciclos de fadiga devido ao seu carregamento.

A vida útil da estrutura é atingida quando o somatório dos danos é igual a 1. Logo, ao calcular a diferença entre o valor unitário e o dano total nas armaduras à flexão à fadiga durante um ano, tem-se a vida útil das mesmas, em anos. A Tabela 3 apresenta o resultado do acúmulo de dano para cada classe de veículo do espectro de (Rossigali, 2013), e a VUF, considerando os coeficientes de ponderação das cargas verticais da (ABNT NBR 7188, 2013).

Tabela 3. Acúmulo de dano e vida útil à fadiga da ponte sobre o Rio Chapecó.

Portanto, a vida útil da ponte sobre o Rio Chapecó, considerando o tráfego de veículos de Rossigali (2013) majorados pelos coeficientes de impacto da (ABNT NBR 7188, 2013), é igual a 14,91 anos, com um dano total acumulado de 6,71E-02 (unidade).

5. ConsideraÇÕes finais

Esse estudo foi desenvolvido com o objetivo de verificar se uma ponte projetada em 1987, conforme as normas vigentes à época (ABNT NBR NB-2, 1961; ABNT 7188, 1984) ainda apresenta segurança à fadiga segundo as normas vigentes atuais (ABNT NBR 7188, 2013; ABNT NBR 6118, 2014). Para tal, estudou-se a situação mais crítica da estrutura - a viga longarina no meio do vão central. Com o desenvolvimento da presente pesquisa foi possível concluir que:

• Na verificação à fadiga das armaduras longitudinais sujeitas à flexão simples, considerando as cargas da (ABNT NBR 7188, 2013), a tensão atuante foi de 190,39 MPa, ou seja, acima do limite especificado pela norma, (180 MPa). Em relação às armaduras transversais, a tensão atuante foi de, aproximadamente, 44 % superior ao limite especificado em norma, também não atendendo aos critérios de segurança à fadiga;
• Na verificação do concreto à compressão, considerando as cargas da (ABNT NBR 7188, 2013), o trecho investigado provou-se seguro, com uma tensão atuante de 3,56 MPa, abaixo do limite de 6,43 MPa. Dessa forma, pode-se concluir que caso a fadiga ocorresse na estrutura, ela aconteceria inicialmente nos estribos, e não no concreto;
• A VUF, devido ao tráfego de veículos reais do espectro de (Rossigali, 2013) e coeficientes majoradores das cargas dinâmicas da (ABNT NBR 7188, 2013), foi de 14,91 anos. Isso, pois os carregamentos vigentes considerados resultaram em tensões muito superiores ao limite à fadiga das armaduras à flexão;
• Após os cálculos de verificação à fadiga pelo método de limitação de tensões e pelo acúmulo de danos, concluiu-se que as armaduras à flexão e os estribos da ponte sobre o Rio Chapecó, não atenderam a verificação à fadiga, apenas o concreto à compressão, considerando o carregamento da (ABNT NBR 7188, 2013). No caso do espectro de veículos reais, as armaduras à flexão não atenderam aos critérios de segurança da regra de Palmgren-Miner (acúmulo de danos).

É importante salientar que apesar das análises terem sido feitas sobre um caso real, as características das cargas (veículos, tráfego) não representam, necessariamente, as reais condições de tráfego sob o qual a ponte está sujeita. Dessa forma, a medição das características dos veículos e do tráfego in situ poderia resultar em idades diferentes de VUF.

Além disso, recomenda-se que um estudo minucioso dos elementos da estrutura seja realizado para uma completa verificação à fadiga, visto que alguns destes estão sujeitos a variações de tensão ao longo de sua extensão. Com isso, uma avaliação global do desempenho poderá ser obtida.

REFERÊNCIAS

Al-Khaiat, H., Fattuhi, N. (2001), Long-term strength development of concrete in arid conditions. Cement and Concrete Composites. 23(4-5)363-373. https://doi.org/10.1016/S0958-9465(01)00004-X

American Concrete Institute, ACI (1997), “ACI 215R-2: Considerations for Design of Concrete Structures Subjected to Fatigue Loading”. Michigan, Estados Unidos.

American Concrete Institute, ACI (2019). “ACI 318: Building Code Requirements for Structural Concrete”. Michigan, Estados Unidos.

Associação Brasileira de Normas Técnicas (1961). NB-2: Cálculo e Execução de Pontes de Concreto Armado. Rio de Janeiro.

Associação Brasileira de Normas Técnicas (1984). NBR 7188: Carga móvel em ponte rodoviária e passarela de pedestre. Rio de Janeiro.

Associação Brasileira de Normas Técnicas (2013). NBR 7188: Carga móvel em ponte rodoviária e passarela de pedestre. Rio de Janeiro.

Associação Brasileira de Normas Técnicas (2013). NBR 15575: Desempenho de edificações habitacionais. Rio de Janeiro.

Associação Brasileira de Normas Técnicas (2014). NBR 6118: Projeto de estruturas de concreto - Procedimento. Rio de Janeiro.

Baroni, H. J. M. (2010), “Simulação da vida útil de fadiga do concreto em vigas de tabuleiro de pontes em função do fluxo de veículos pesados”, Tese de Doutorado em Engenharia, Universidade Federal do Rio Grande do Sul, Porto Alegre.

cap. 1 Bolotin, V. V. (1998), Introduction. In: Bolotin V. V. “Mechanics of Fatigue”, Boca Raton, CRC Press LLC, , pp. 01-17.

Branco, F., Paulo, P. (2012), O projecto de pontes para vidas superiores a 100 anos. Revista ALCONPAT. 2(1):1-9. http://dx.doi.org/10.21041/ra.v2i1.20

Callister J., William D. (2008), “Ciência e engenharia de materiais: Uma introdução”. LTC, Rio de Janeiro, Brasil, p. 620. Tradução: Soares, S. M. S.

Cervo, T. C. (2004), “Estudo da resistência à fadiga de concretos de cimento Portland para pavimentação”, Tese de Doutorado em Engenharia, Universidade de São Paulo, São Paulo.

Confederação Nacional de Transporte, CNT (2018), “Pesquisa CNT de rodovias 2018: Relatório gerencial”. Brasília, Brasil.

Comité Euro-International du Betón, CEB (1988), “Fatigue of Concrete Structures. Bulletin d’Information Nº. 188”. Dubrovnik, Croácia.

Departamento de Estradas de Rodagem de Santa Catarina, DER (1987), “Projeto da Ponte sobre o Rio Chapecó na rodovia SC 451, entre os municípios de Xaxim e São Domingos”. Florianópolis, Brasil.

Departamento Nacional de Infraestrutura e Transporte, DNIT (2005), “Manual de Conservação Rodoviária”. Rio de Janeiro, Brasil.

Elaty, M. A. A. A. (2014), Compressive strength prediction of Portland cement concrete with age using a new model. HBRC Journal. 10(2)145-155. https://doi.org/10.1016/j.hbrcj.2013.09.005

Fan, Z., Sun, Y. (2019), Detecting and evaluation of fatigue damage in concrete with industrial computed tomography technology. Construction and Building Materials. 223:794-805. https://doi.org/10.1016/j.conbuildmat.2019.07.016

Fathalla, E., Tanaka, Y., Maekawa, K. (2018), Remaining fatigue life assessment of in-service road bridge decks based upon artificial neural networks. Engineering Structures. 171:602-616. https://doi.org/10.1016/j.engstruct.2018.05.122

Boletim Técnico da Escola Politécnica da USP, BT/PCC (2000), “Concreto com Fibras de Aço - Boletim Técnico PCC/260”. São Paulo, Brasil.

Access in 15 Mar. 2018 Ftool (2018), “A Graphical-Interactive Program for Teaching Structural Behavior”. Available in: <https://www.ftool.com.br/Ftool/>. .

Gao, Q., Dong, Z., Cui, K., Liu, C., Liu, Y. (2020), Fatigue performance of profiled steel sheeting-concrete bridge decks subjected to vehicular loads. Engineering Structures. 213:110558. https://doi.org/10.1016/j.engstruct.2020.110558

Hobbacher, A. F., Hicks, S. J., Karpenko, M., Franz, T., UY, B. (2016), Transfer of Australasian bridge design to fatigue verification system of Eurocode 3. Journal of Constructional Steel Research. 122:532-542. https://doi.org/10.1016/j.jcsr.2016.03.023

Meneghetti, L. C. (2007), “Análise do comportamento à fadiga de vigas de concreto armado reforçadas com PRF de vidro, carbono e aramida”, Tese de Doutorado em Engenharia, Universidade Federal do Rio Grande do Sul, Porto Alegre.

Nussbaumer, A., Borges, L., Davaine, L. (2011), “Fatigue design of steel and composite structures”. Wiley, Hoboken, Estados Unidos, p. 167.

Pfeil, W. (1979), “Pontes em concreto armado: Elementos de projeto, solicitações, dimensionamento”. LTC, Rio de Janeiro, Brasil, p. 433.

Pfeil, W. (1989), “Concreto armado”. LTC, Rio de Janeiro, Brasil, p. 812.

Rossigali, C. E. (2013), “Atualização do modelo de cargas móveis para pontes rodoviárias de pequenos vãos no Brasil”, Tese de Doutorado em Engenharia Civil, Universidade Federal do Rio de Janeiro, Rio de Janeiro.

Santos, L. A., Pfeil, M. S. (2014), Desenvolvimento de modelo de cargas móveis para verificação de fadiga em pontes rodoviárias. Engenharia Estudo e Pesquisa ABPE 14(1):40-47.

Santos, L. F. (2013), “Desenvolvimento de um modelo de cargas móveis para verificação de fadiga em pontes rodoviárias”, Trabalho de Conclusão de Curso em Engenharia Civil, Universidade Federal do Rio de Janeiro, Rio de Janeiro.

Silva, C. J. G., Monteiro, E. C. B., Vitório, J. P. A. (2018), Condições estruturais e funcionais de pontes e viadutos das rodovias federais de Pernambuco. Revista ALCONPAT. 8(1)79-93. http://dx.doi.org/10.21041/ra.v8i1.199

Süssekind, J. C. (1980), “Curso de Concreto: Concreto Armado - Volume I”. Globo, Porto Alegre, Brasil, p. 376.

Toledo, R. L. S. (2011), “Avaliação de vida útil à fadiga em ponte mista aço-concreto considerando o espectro de veículos reais”, Trabalho de Conclusão de Curso em Engenharia, Universidade Federal do Rio de Janeiro, Rio de Janeiro.

Yadav, I. N., Thapa, K. B. (2020), Fatigue damage model of concrete materials. Theoretical and Applied Fracture Mechanics. 108:102578. https://doi.org/10.1016/j.tafmec.2020.102578