| Applied Research | https://doi.org/10.21041/ra.v11i2.515 |
Safety verification of fatigue of a reinforced concrete bridge according to ABNT NBR 6118 2014
Verificação de Segurança à fadiga de pontes em concreto armado conforme ABNT NBR 6118, 2014.
Verificación de seguridad de la fatiga de puentes en hormigón armado según ABNT NBR 6118:2014
M. D.
Rossato1
*,
G. S. Munhoz2
![]() , R. B. P.
dos Santos1,
L. M. O.
Scoz1
, R. B. P.
dos Santos1,
L. M. O.
Scoz1
1 Departamento de Engenharia Civil, Escola do Mar, Ciência e Tecnologia, Universidade do Vale do Itajaí - UNIVALI, Itajaí, Brasil.
2 Departamento de Construção Civil, Universidade Federal do Paraná - UFPR, Curitiba, Brasil.
*Contact author: mateusrossato.engcivil@gmail.com
Reception: September 16, 2020.
Acceptance: January 20, 2021.
Publication: May 01, 2021.
| Cite as: Rossato, M. D., Munhoz, G. S., P. dos Santos, R. B., Scoz, L. M. (2021), "Safety verification of fatigue of a reinforced concrete bridge according to ABNT NBR 6118,2014.", Revista ALCONPAT, 11 (2), pp. 109 – 123, DOI: https://doi.org/10.21041/ra.v11i2.515 |
Abstract
In this case study, the fatigue security of a bridge designed in 1987 was examined considering the current Brazilian standard. A structural model was developed to determine and verify fatigue security in the most critical section considering the Brazilian Load Model and the literature’s vehicle spectrum. According to the stress variation method, it concludes that the concrete submitted to compression meets the minimum criteria, but the steel section is not enough to resist shearing and flexural stresses. Pursuant to the Palmgren-Miner rule, the fatigue service life of the reinforcement’s bars under flexural stress is 14,91 years. A more detailed structural analysis of the bridge and the vehicle spectrum is necessary to confirm these results.
Keywords:
fatigue,
bridge,
Palmgren-Miner rule,
service life.
Resumo
Nesse estudo de caso, a segurança à fadiga de uma ponte projetada em 1987 foi verificada segundo a norma vigente brasileira. Elaborou-se um modelo estrutural para determinar e verificar a seção mais crítica considerando o trem-tipo e o espectro de veículos da literatura. Segundo o método de limitação de variação de tensões, conclui-se que o concreto sujeito à compressão atende aos critérios, mas a área de aço não é suficiente para combater os esforços cortante e de flexão. Pela regra de Palmgren Miner, a vida útil à fadiga nas armaduras sujeitas à flexão é de 14,91 anos. Uma análise mais detalhada da estrutura e do espectro de veículos é necessária para reiterar tais resultados.
Palavras-chave:
fadiga,
ponte,
regra de Palmgren-Miner,
vida útil.
Resumen
En este estudio, se verificó la seguridad a la fatiga de un puente proyectado en 1987 según la normativa brasileña vigente. Se construyó un modelo estructural para determinar y verificar la sección más crítica considerando el modelo estándar brasileño y el espectro de vehículos en la literatura. Según el método de variación de esfuerzos, se concluye que el hormigón sometido a compresión cumple con los criterios, pero la sección de acero no es suficiente para resistir los esfuerzos cortantes y de flexión. Por la regla de Palmgren-Miner, la vida útil a la fatiga de las armaduras sometidas a flexión es de 13,91 años. Es necesario un análisis más detallado de la estructura y del espectro de carga para confirmar estos resultados.
Palabras clave:
fatiga,
puente,
regla de Palmgren-Miner,
vida útil.
1. Introduction
In Brazil, the transportation of assets and people is mostly carried in a huge network of roads, with approximately 1.7 million kilometers extent. The movement of loads in this mode of transport corresponds to 61% of the national transport matrix (CNT, 2018). In this context, (Baroni, 2010) argues that “Special Engineering Structures” (SES) - such as bridges and viaducts - are pivotal elements of the transportation system. Therefore, ensuring its functionality, safety and durability is significant.
In the last decades, the lack of maintenance and repairing policies for SES in Brazil has contributed to accelerate the deterioration process of these structures. Several Brazilian bridges were built between the 50s and 70s and, therefore, were designed by standards that did not foresee the current loadings, nor the current traffic intensity (Silva et.al., 2018).
The main damages that compromise the performance of SES are related to corrosion, physical impact, and erosion of foundations. Nevertheless, (Fathalla et.al., 2018) point out that the bridges and viaducts service life is also directly associated with cyclical stress variations due to vehicle traffic. (Hobbacher et.al., 2016) point out that after a certain number of loading-unloading cycles,
cracks are formed and propagated, and this can lead to the collapse of the structure due to fatigue. (Gao et.al., 2020) studied the fatigue service life (FSL) of bridges with steel-concrete composite structures and observed that, in this case, the strength of the concrete had a small impact in FSL’s determination. This was reiterated by (Santos, 2013), who proved that fatigue collapse can happen with stresses lower than the elastic limit of the steel-concrete composition.
The Brazilian standard (ABNT NBR 6118, 2014) is used to evaluate damage to concrete structures due to cyclical actions. This standard determines the criteria that must be adopted to check the ultimate fatigue limit state (unlimited life method) and the limit service state. In this case, the verification of fatigue through stress limitation is preferably recommended, adopting loadings presented in (ABNT NBR 7188, 2013).
The proposed loading by the Brazilian standard (ABNT NBR 7188, 2013), which approaches mobile loads for bridges and replaced (ABNT NBR 7188, 1984), does not present configurations about the real traffic flow, but a hypothetical Brazilian Load Model. In addition, it is provided an evenly distributed load per unit area, aiming to represent light vehicles or crowds’ transit. Exceptionally, if the load spectrum is available, the Palmgren-Miner rule can be used. This allows to determine the fatigue service life. According to this method, it is assumed that the damage due to fatigue accumulates linearly with the number of cycles and these damages are, according to (Fan and Sun, 2019), the deterioration process that reduces the cross-sectional resistant area.
This study was developed to verify the fatigue security of a bridge designed in 1987 according to (ABNT NBR 6118, 2014). Two methods were used, the limitation of stress variation and fatigue service life. The most critical section of the structure was studied - the girder beam in the middle of the central span.
2. Contextualization
2.1. The fatigue mechanism in the deterioration of bridges
According to (Yadav and Thapa, 2020), fatigue is a mechanism of structural failure that occurs in a material subjected to repetitive stress variations, that is, which oscillate intermittently during a certain time interval. The set of loading and unloading actions is called cycle. Several cycles culminate with the appearance of new micro cracks or with the propagation of pre-existing ones, which can cause the structure collapse (Cervo, 2004). The greater the magnitude of intermittent loads, the smaller the number of cycles required to fail the structure (BT / PCC, 2000).
Bridges and viaducts are structures subjected to fatigue due to the accumulation of damage from non-uniform cycles of stress variation caused by the traffic flow of vehicles with different characteristics. The analysis of this phenomenon in SES structures, especially in situations of intermittent traffic, is essential to guarantee structural security (Santos and Pfeil, 2014).
(Callister and William, 2008) affirm that fatigue rupture is brittle. There is little (or none) plastic deformation. In general, the collapse occurs with the propagation of cracks, and when the fracture surface is perpendicular to the direction of the stress application. However, in the concrete realm, (Euro-International du Béton Committee, 1988) argues that there is not an exclusive collapse due to fatigue. In this case, the rupture of the concrete structure occurs due to the progressive deterioration of cracks caused by cyclic loading.
Considering reinforced concrete structures, (Meneghetti, 2007) proved that fatigue in reinforcement’s bars is not usually a relevant factor. However, due to the increase of structures subjected to cyclic loads designed based on rupture state (ultimate limit state), it is important that the effects associated with fatigue are analyzed.
2.2. Durability and fatigue service life
The standard (ACI 318, 2019) emphasizes that the structures’ durability concerns to the ability to resist degradation processes, preserving its integrity when submitted to the environment where it was designed. In this context, the Brazilian standard (ABNT NBR 15575, 2013) defines project’s service life (PSL), as the time interval in which the structure maintains its durability and performance requirements, meeting the objectives that were proposed.
According to (Branco and Paulo, 2012), a structure achieves its PSL when pathological manifestations (aesthetic or structural) which impair its performance are detected. However, there are maintenance operations that allow restoring the service life of damaged structures.
Unlike the term PSL, which addresses the service life of the structure, FSL is more restricted and is specifically associated with the time interval required for cyclical stresses to promote and propagate cracking in the structural element. (Baroni, 2010) argues that the FSL does not necessarily culminate with the structure collapse, but with cracks in critical dimensions that can be the indirect object of failure. Thus, along the PSL of bridges and viaducts, vehicle transit should not promote excessive stress variations that weakens the structure regarding fatigue.
3. Methodology
3.1. Characterization of the bridge over the Chapecó River
The bridge over the Chapecó River was designed in 1987, with the objective of connecting the cities of Xaxim and São Domingos, both in the state of Santa Catarina - Brazil. The bridge studied has a total extension of 170 m (longitudinally), distributed in 3 central spans of 33,60 m, 2 spans of 28,00 m (one for each side) and 2 spans of 6,60 m, one in each extremity.
The bridge deck has a total width of 9,00 m, of which 7,20 m is for the rolling tracks, and two lanes with 0,90 m (one at each edge) are intended for pedestrians and cyclists. The deck slab is supported by two girders (30x170 cm), six beams of section 30 x 170 cm (one at each support), and ten beams of section 30 x 170 cm (two in each span - except for the end spans). The cross section of the central span of the bridge is illustrated in Figure 1A. To construct the beams and girders a concrete with a characteristic compressive strength of 20 MPa and CA-50 steel as reinforcement was used.
A preliminary structural analysis about the bridge revealed that the most critical fatigue-based condition occurs in the middle of the central spans of the bridge. Therefore, it was decided to determine the FSL of the girder present in this section (Figure 1B).
3.2. Determination of active stresses
The structural model was built considering the permanent and mobile loads, and the respective weighting coefficients of vertical loads (WCV), according to (ABNT NBR 7188, 2013). The determination of the influence and envelope lines was made using the software Ftool (2018), which performs structural analysis in a 2D-level.
As recommended by the Brazilian standard (ABNT NBR 6118, 2014) to verify the fatigue, the stresses applied on concrete and steel were determined in the elastic region and the calculation of the compound flexural stresses in the second deformation stage - disregarding the concrete tensile strength. Regarding the bending moments, the combination of actions for the service limit state (SLS) to fatigue was adopted, recommended by the aforementioned standard.
To determine the resistant moment and the other stresses on the structure, the balance of forces equations and those from (Pfeil, 1989) were used, respectively. As for the calculation of the stresses on the longitudinal reinforcement’s bars and concrete, the equations (1) - (2), from (Süssekind, 1980), and Equation (3) from (ABNT NBR 6118, 2014) were adopted to the transverse reinforcement’s bars (α = 90º).
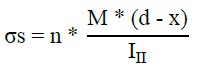 |
(1) |
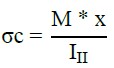 |
(2) |
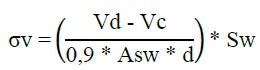 |
(3) |
Where "σs" represents the stress in the reinforcement’s bars submitted to tensile (kN/cm²); n is the division between the elasticity module of steel and concrete; M is the moment of inertia (kN.cm); d is the distance from the compressed portion to the gravity center of the reinforcement’s bars submitted to tensile (cm); x is the neutral line (cm); III represents the equivalent inertia in the second deformation stage (cm4); "σc" is the compressive stress in concrete (kN/cm²); "σv" is the stress in the transverse reinforcement’s bars (α = 90º) (kN/cm²); Vd is the effort shearing of a project over the stirrups (kN); Vc is the effort shearing absorbed by complementary mechanisms (concrete); and, Asw is the transversal steel area necessary over 1 m (cm²/m).
A structural analysis revealed that the center of the largest span of the structure had the biggest stress variation to the reinforcement’s bars subjected to bending and shearing, and for concrete subjected to simple compression. Thus, the fatigue verification - according to (ABNT NBR 6118, 2014) criteria - was made about this section (critical condition). As for the stress variation, this is the difference between the maximum and the minimum stresses calculated, if these values have opposite signs, the difference will be between 0 (zero) and the highest value in module. In case of bridges, this variation in tension will be the relation between the active stresses due to permanent loads and those caused by mobile loads plus permanent loads.
In addition, the structural model was created considering the loads specified in (ABNT NBR 7188, 1984 and NB-2, 1961), to prove that the bridge was designed according to the standards of that time (1987). This also made possible to validate the method of calculating the reinforcement’s bars using the strength balance equations and the representative model of the bridge.
3.3. Fatigue security verification
The fatigue security verification of the bridge was made according to the guidelines of (ABNT NBR 6118, 2014) by two methodologies: stress limitation and fatigue’s service life. The first methodology should be considered the verification by the ultimate limit state (ULS) to fatigue (unlimited life method) and service limit state should be considered. In this work, the analysis will be carried only in the ULS.
3.3.1 Stress limitation
The verification of safety due to fatigue by the stress limitation method was made according to the current regulations to evaluate the security of the structure considering damages caused by cyclical actions. This verification followed all the recommendations of (ABNT NBR 6118, 2014), and was made considering the frequent combination of actions, according to (ABNT NBR 8681, 2004). The calculation of mobile loads was made according to the train-model of (ABNT NBR 7188, 2013), positioned at the most unfavorable point of the structure.
As recommended (ABNT NBR 6118, 2014), the verification was made on the concrete submitted to compression and on reinforcement’s bars subjected to bending and shearing. The structural analysis did not identify tension efforts at the studied point, therefore, the security verification of the concrete subjected to tension was neglected.
3.3.2 Fatigue service life
The FSL verification of the bridge was made to the reinforcement’s bars subjected to bending, in the middle of the largest span. This was based on the guidelines from (ABNT NBR 6118, 2014), which presents the S-N curve for the bars of reinforced concrete structures. According to (Bolotin, 1998), fatigue curves were introduced in 1860 by the German August Wӧhlner. The curve relates the magnitude of the stress cycles and the number of cycles required to bring the material to rupture.
According to (ABNT NBR 6118, 2014), to use a real spectrum of loads (or from the literature), it must consider the Palmgren-Miner rule, which relates N (number of cycles to collapse the structure due to fatigue, for a certain stress variation) with the number of cycles experienced (n). Thus, the calculation of FSL is given by Equation (4). According to (ACI 215R-74, 1997; Nussbaumer et. Al., 2011), fatigue damage must be accumulated linearly, assuming the end of service life when this sum is equal to 1.
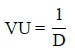 |
(4) |
Where VU represents the service life; and D, the accumulated damage.
For the frequency of vehicle flow, the model presented by (Rossigali, 2013) was adopted. And, regarding the number of steel’s N cycles (damage), it was calculated according to Equations (5) - (6), proposed by (Bolotin, 1998) and derived from the S-N curves such as the one in (ABNT NBR 6118, 2014).
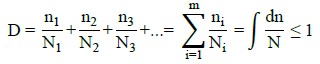 |
(5) |
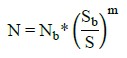 |
(6) |
Where D represents the accumulated damage; n i is the number of cycles applied to the i-th stress level; N i is the fatigue life of the i-th stress level that corresponds to the number of cycles until the failure of this level; N is the number of cycles associated with fatigue failure; Nb is a dimensionless constant from the S-N curves that arises from (ABNT NBR 6118, 2014); Sb is a constant with a unit of tension; S is the stress in the material; and, m is the exponent of the fatigue curve.
All load’s values for each vehicle were increased by the WCV from (ABNT NBR 7188, 2013). Therefore, the loading for each type of traffic spectrum (according to the literature) was considered individually, closely to the structure's weight, determining the maximum and minimum bending moments in the middle of the largest span.
According to (ABNT NBR 6118, 2014), it was adopted the index of the elasticity modulus of steel (Es) and concrete (Ec) as 10; and the damage caused by vehicles with loads below 30 kN was ignored. As for the neutral line (XII) and the inertia (III) of the section in the second deformation stage, and the distance from the compressed section of the beam to the reinforcement’s bars gravity center submitted to tensile stresses (d), these will be the same as those used in the fatigue verification by limiting the stress variation.
Given that the FSL determination was performed for the girder reinforcement’s bars submitted to flexural stresses, Equation 1 was used to determine the tension due its own weight and to vehicle loads.
As for the characterization of the vehicle spectrum, this was based on the literature, to determine the active loading on the structure and the FSL. Considering the impossibility of measuring the current vehicle traffic, the database described by (Rossigali, 2013; Santos, 2013) was used. According to the authors, the heavy commercial vehicle traffic can be represented by 27 classes with different dimensions (longitudinal and transversal), different distances between axles, and different loads per axle. An example of the characteristics from one of the 27 classes studied (2CC) is presented in Table 1. The characterization of heavy vehicles that travel on the Brazilian road system, described by (Rossigali, 2013; Santos, 2013), was made at different intervals (1999 - 2011) and with different aids from different highway administrators.
| Table 1. Relative frequency of vehicle class 2CC, by weight range. | ||||||||||||||
 | ||||||||||||||
The vehicle type (according to the class) and the number of vehicles (in each class) directly influence the intensity of the bending moments, stress cycle and, consequently, the damage due to fatigue. The volume of vehicles in each class was determined by multiplying the average daily volume of vehicles by the absolute frequency (in each weight range, for each class).
According to (Rossigali, 2013), highways with only one lane per direction (such as the bridge studied here) have an average daily volume of 6 thousand vehicles per day. The absolute frequency represents the number of observations in each range regarding the total number of observations. The relative frequency is the relation between the volume of vehicles from the same class. The total number of vehicles in each class is shown in Table 2.
| Table 2. Vehicle volume for each of the 27 classes (considering all ranges). | ||||||||||||||
| Class | Volume (vehicles) | Class | Volume (vehicles) | Class | Volume (vehicles) | Class | Volume (vehicles) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2CC | 663,96 | 3C3 | 15,30 | 2I3 | 22,26 | 3T4 | 278,40 | |||||||
| 2C | 745,32 | 3D4 | 9,60 | 3S1 | 10,14 | 3T6 | 51,18 | |||||||
| 3C | 1026,96 | 2S1 | 268,92 | 3S2 | 44,52 | 3M6 | 10,02 | |||||||
| 4C | 8,70 | 2S2 | 718,08 | 3S3 | 368,82 | 2CB | 477,12 | |||||||
| 2C2 | 89,88 | 2S3 | 681,24 | 3I1 | 12,72 | 3CB | 122,16 | |||||||
| 2C3 | 16,62 | 2I1 | 8,82 | 3I2 | 7,86 | 3BB | 122,16 | |||||||
| 3C2 | 17,10 | 2I2 | 106,98 | 3I3 | 95,16 | - | - | |||||||
| Total | 6000 | |||||||||||||
The position of the vehicles also influences the stress diagram. In this work, the position of the vehicles (according to the literature spectrum), was adopted in the center of the lane as recommended by (National Department of Infrastructure and Transport, 2005) and (Toledo, 2011). For the envelope of efforts, the loads due to traffic were increased by WCV, proposed by (ABNT NBR 7188, 2013).
4. Results and discussion
4.1. Girder mechanical properties
The resistant section (width) of the girder flange, neutral line and inertia were determined in the second deformation stage. With these results, the structure resistant moment was calculated so that structural reinforcement’s bars could be made. (in case it was smaller than the bending moments due to the loads from (ABNT NBR 7188, 2013)).
This way, given that the flange width of the girder is 401,60 cm, the neutral line of the section in the ultimate limit state (x) is 10,35 cm, the neutral line of the section in Deformation Stage II (x2) is 32, 45 cm, the moment of inertia (Mk) is 6.512,37 kN.m and the resistant moment (I2) is equal to 4.05x107 cm4.
Considering that the bridge was designed according to (ABNT NBR 7188, 1984) (current standard at the time when the project was designed), the structure was analyzed considering the permanent loads (Brazilian Load Model equal to 300 kN), and the impact coefficient (φ) of 1,23, specified in (ABNT NBR NB-2, 1961), as indicated by (Pfeil, 1979). The result is shown in Figure 2.
 |
||||
| Figure 2. Envelopment of efforts due to the 300 Brazilian Load Model and φ = 1.23. | ||||
The bending moment in the middle of the central span is 6.720,64 kN.m, therefore, close to that calculated using the balance equations of forces, with a difference of 208.27 kN.m, or approximately 3.2%. In this way, it is attested that the bridge was designed according to the standards of that time (1987). The methodology to calculate the strength of the reinforcement’s bars was validated by the balance of forces equations and the representative model of the bridge structure.
4.2. Fatigue verification
The fatigue efforts were determined according to the loadings of (ABNT NBR 7188, 2013). After determining the permanent loads, the Brazilian Load Model (TB-450 kN) and the crowd load were increased by the WCV (WCV = 1.60), obtaining maximum and minimum shear forces (467,43 kN and -467,38 kN, respectively) and maximum bending moments (8.904,07 kN.m) and minimum (1.083,10 kN.m), as shown in Figures 3 and 4, in the middle of the largest span of the bridge.
 |
||||
| Figure 3. Shearing envelope with TB-450 increased by WCV (ABNT NBR 7188, 2013). | ||||
 |
||||
| Figure 4. Bending moment envelope with TB-450 increased by WCV (ABNT NBR 7188, 2013). | ||||
Therefore, it was performed the fatigue verification about the bridge over the Chapecó River, considering the recommendations of (ABNT NBR 6118, 2014) for reinforcement’s bars subject to bending, compressed concrete and for shear reinforcement’s bars (stirrups).
4.2.1 Flexural reinforcement
The verified section of the girder has 24 steel bars with a diameter equal to 22,2 mm (Steel area = 92,90 cm²). For this diameter, (ABNT NBR 6118, 2014) recommends that the stress in the reinforcement’s bars must be limited to ∆fsd,fad = 180 MPa. Thus, considering the mechanical properties of the studied girder section, it was performed a fatigue analysis for reinforcement’s bars submitted to flexural moments in the middle of the largest span of the bridge over the Chapecó River, considering the loads of 450 kN (Brazilian model) and the weighting coefficients of the vertical loads from (ABNT NBR 7188, 2013).
To determine the maximum and minimum stresses on the bars, Equation 1 was adopted. In the section investigated, the stress variation (σsmax - σsmin) was 190,39 MPa, in other words, bigger than the limit (180 MPa) for 22,2 mm bars. Therefore, this section is not safe against fatigue.
4.2.2 Concrete in compression
The fatigue verification for the concrete in the middle of the bridge span was performed only with compressive loadings because this represents a real situation. According to (ABNT NBR 6118, 2014) this tension must be limited to 45% of the concrete project resistance. In addition, the tensions must be obtained in a distance no longer than 30 cm from the compressed section. Thus, given that the neutral line at the second deformation stage was equal to 32,45 cm, tension variation was corrected by triangle similarity.
To determine the stress variation caused by the maximum and minimum moments in the middle of the largest span of the structure, Equation 2 was used. The compressive stress variation at this point was equal to 3,56 MPa, lower than the standardized limit (6,43 MPa). In this way, the compressed concrete section is safe against fatigue.
It is important to note that, according to (Al-Khaiat and Fattuhi, 2001; Elaty, 2014), concrete has gained resistance over the years. This resistance gain depends on variables such as water/cement ratio, exposure conditions (temperature, humidity) and curing regime. Despite a higher strength, the concrete contributes to reducing the damage associated with fatigue. This consideration could not be included in the present study due to administrative limitations. Thus, this verification assumed the worst-case scenario, that is, keeping the concrete resistance constant.
4.2.3 Shear reinforcement’s bars
The girder section under investigation has steel stirrups ϕ10.0 mm (steel area = 4,62 cm² / m), spaced at 17 cm. For this diameter, (ABNT NBR 6118, 2014) recommends that the tension be limited to ∆fsd,fad = 85 MPa. As addressed by (Pfeil, 1979), the shear stress variation in the middle of the longest span of the bridge was 467,43 kN to -467,38 kN. However, the tensions must be considered ranging from 0 (zero) to the maximum value, in this case 467,43 kN.
To determine the stress variation in shear reinforcement’s bars, Equation 3 was adopted, according to (ABNT NBR 6118, 2014). Regarding efforts, they were corrected for the combination according to the service limit state (SLS) to fatigue.
The stress variation in reinforcement’s bars for shear efforts (stirrups) was 122,26 MPa. This value is higher than the limit (85 MPa) for ϕ10.0 mm bars, according to (ABNT NBR 6118, 2014). Therefore, the section under shear is not safe against fatigue.
4.3. Accumulated damage and fatigue service life
The calculation of the damage must consider the tensions due to the real vehicle spectrum and the S-N curve (Wöeller Curve), from (ABNT NBR 6118, 2014), as described by Equation 6. The tension limit value was calculated based on reinforcement’s bars type T1, which according to (ABNT NBR 6118, 2014) has an S-N curve with angular coefficients of k1 = 5 and k2 = 9. The limit number of cycles to fatigue adopted was N = 1x106 cycles. This number represents the point of change in the slope of the S-N curve. Therefore, the tension limit value was 194,41 MPa.
For values of stress variation lower than 194,41 MPa, it will be considered the curve stretch with a slope equal to 9. For variations above the limit value of N = 1x106, a slope equal to 5 will be adopted. Considering Equation 5 with Nb equal to 1x106 cycles, Sb equal to 194,41 MPa, exponent of the fatigue curve (m) varying between 5 and 9 and the tension in the material (S) due to each weight range for each vehicle class, the number of cycles N to fatigue was determined.
Then, adopting the traffic volume equal to 6.000 vehicles / day (2,19 million/year), it was calculated the damage in the structure and the accumulation of damage per year (D ano ), according to the Palmgren rule Miner (Equation 5), that is, the summation of the division between the number of vehicles in each class and weight range that transited for one year and the number of fatigue cycles due to their loading.
The service life of the structure is reached when the summation of the damages is equal to 1. Therefore, the difference between the unitary value and the total damage in the reinforcement’s bars submitted to fatigue for a year, determines the service life, in years. Table 3 shows the damage accumulation for each vehicle class in the spectrum of (Rossigali, 2013), and the FSL, considering the weighting coefficients of the vertical loads from (ABNT NBR 7188, 2013).
| Table 3. Accumulation of damage and fatigue service life of the bridge over the Chapecó River. | ||||||||||||||
 | ||||||||||||||
Therefore, the service life of the bridge over the Chapecó River, considering the vehicle traffic of Rossigali (2013) increased by the impact coefficients of (ABNT NBR 7188, 2013), is equal to 14,91 years, with an accumulated total damage of 6,71E-02.
5. Conclusions
This study was developed to verify if a bridge designed in 1987, according to the current standards at that time (ABNT NBR NB-2, 1961; ABNT 7188, 1984) is still safe against fatigue considering the current standards (ABNT NBR 7188, 2013; ABNT NBR 6118, 2014). The most critical situation of the structure was studied - the girder in the middle of the central span. It was possible to draw the following conclusions:
It is important to note that although the analyses were made on a real case, the loads characteristics (vehicles, traffic) does not necessarily represent the real traffic conditions to which the bridge is subjected. Thus, measuring vehicle characteristics and traffic in situ could result in different ages of FSL.
In addition, it is recommended that a thorough study of the structure is performed for an overall assessment of fatigue, as long as some of the other elements are also subjected to relevant stress variations. Therewith, a global analysis is required for a better understanding of fatigue behavior.
References
Al-Khaiat, H., Fattuhi, N. (2001), Long-term strength development of concrete in arid conditions. Cement and Concrete Composites. 23(4-5)363-373. https://doi.org/10.1016/S0958-9465(01)00004-X
American Concrete Institute, ACI (1997), “ACI 215R-2: Considerations for Design of Concrete Structures Subjected to Fatigue Loading”. Michigan, Estados Unidos.
American Concrete Institute, ACI (2019). “ACI 318: Building Code Requirements for Structural Concrete”. Michigan, Estados Unidos.
Associação Brasileira de Normas Técnicas (1961). NB-2: Cálculo e Execução de Pontes de Concreto Armado. Rio de Janeiro.
Associação Brasileira de Normas Técnicas (1984). NBR 7188: Carga móvel em ponte rodoviária e passarela de pedestre. Rio de Janeiro.
Associação Brasileira de Normas Técnicas (2013). NBR 7188: Carga móvel em ponte rodoviária e passarela de pedestre. Rio de Janeiro.
Associação Brasileira de Normas Técnicas (2013). NBR 15575: Desempenho de edificações habitacionais. Rio de Janeiro.
Associação Brasileira de Normas Técnicas (2014). NBR 6118: Projeto de estruturas de concreto - Procedimento. Rio de Janeiro.
Baroni, H. J. M. (2010), “Simulação da vida útil de fadiga do concreto em vigas de tabuleiro de pontes em função do fluxo de veículos pesados”, Tese de Doutorado em Engenharia, Universidade Federal do Rio Grande do Sul, Porto Alegre.
cap. 1 Bolotin, V. V. (1998), Introduction. In: Bolotin V. V. “Mechanics of Fatigue”, Boca Raton, CRC Press LLC, , pp. 01-17.
Branco, F., Paulo, P. (2012), O projecto de pontes para vidas superiores a 100 anos. Revista ALCONPAT. 2(1):1-9. http://dx.doi.org/10.21041/ra.v2i1.20
Callister J., William D. (2008), “Ciência e engenharia de materiais: Uma introdução”. LTC, Rio de Janeiro, Brasil, p. 620. Tradução: Soares, S. M. S.
Cervo, T. C. (2004), “Estudo da resistência à fadiga de concretos de cimento Portland para pavimentação”, Tese de Doutorado em Engenharia, Universidade de São Paulo, São Paulo.
Confederação Nacional de Transporte, CNT (2018), “Pesquisa CNT de rodovias 2018: Relatório gerencial”. Brasília, Brasil.
Comité Euro-International du Betón, CEB (1988), “Fatigue of Concrete Structures. Bulletin d’Information Nº. 188”. Dubrovnik, Croácia.
Departamento de Estradas de Rodagem de Santa Catarina, DER (1987), “Projeto da Ponte sobre o Rio Chapecó na rodovia SC 451, entre os municípios de Xaxim e São Domingos”. Florianópolis, Brasil.
Departamento Nacional de Infraestrutura e Transporte, DNIT (2005), “Manual de Conservação Rodoviária”. Rio de Janeiro, Brasil.
Elaty, M. A. A. A. (2014), Compressive strength prediction of Portland cement concrete with age using a new model. HBRC Journal. 10(2)145-155. https://doi.org/10.1016/j.hbrcj.2013.09.005
Fan, Z., Sun, Y. (2019), Detecting and evaluation of fatigue damage in concrete with industrial computed tomography technology. Construction and Building Materials. 223:794-805. https://doi.org/10.1016/j.conbuildmat.2019.07.016
Fathalla, E., Tanaka, Y., Maekawa, K. (2018), Remaining fatigue life assessment of in-service road bridge decks based upon artificial neural networks. Engineering Structures. 171:602-616. https://doi.org/10.1016/j.engstruct.2018.05.122
Boletim Técnico da Escola Politécnica da USP, BT/PCC (2000), “Concreto com Fibras de Aço - Boletim Técnico PCC/260”. São Paulo, Brasil.
Access in 15 Mar. 2018 Ftool (2018), “A Graphical-Interactive Program for Teaching Structural Behavior”. Available in: <https://www.ftool.com.br/Ftool/>. .
Gao, Q., Dong, Z., Cui, K., Liu, C., Liu, Y. (2020), Fatigue performance of profiled steel sheeting-concrete bridge decks subjected to vehicular loads. Engineering Structures. 213:110558. https://doi.org/10.1016/j.engstruct.2020.110558
Hobbacher, A. F., Hicks, S. J., Karpenko, M., Franz, T., UY, B. (2016), Transfer of Australasian bridge design to fatigue verification system of Eurocode 3. Journal of Constructional Steel Research. 122:532-542. https://doi.org/10.1016/j.jcsr.2016.03.023
Meneghetti, L. C. (2007), “Análise do comportamento à fadiga de vigas de concreto armado reforçadas com PRF de vidro, carbono e aramida”, Tese de Doutorado em Engenharia, Universidade Federal do Rio Grande do Sul, Porto Alegre.
Nussbaumer, A., Borges, L., Davaine, L. (2011), “Fatigue design of steel and composite structures”. Wiley, Hoboken, Estados Unidos, p. 167.
Pfeil, W. (1979), “Pontes em concreto armado: Elementos de projeto, solicitações, dimensionamento”. LTC, Rio de Janeiro, Brasil, p. 433.
Pfeil, W. (1989), “Concreto armado”. LTC, Rio de Janeiro, Brasil, p. 812.
Rossigali, C. E. (2013), “Atualização do modelo de cargas móveis para pontes rodoviárias de pequenos vãos no Brasil”, Tese de Doutorado em Engenharia Civil, Universidade Federal do Rio de Janeiro, Rio de Janeiro.
Santos, L. A., Pfeil, M. S. (2014), Desenvolvimento de modelo de cargas móveis para verificação de fadiga em pontes rodoviárias. Engenharia Estudo e Pesquisa ABPE 14(1):40-47.
Santos, L. F. (2013), “Desenvolvimento de um modelo de cargas móveis para verificação de fadiga em pontes rodoviárias”, Trabalho de Conclusão de Curso em Engenharia Civil, Universidade Federal do Rio de Janeiro, Rio de Janeiro.
Silva, C. J. G., Monteiro, E. C. B., Vitório, J. P. A. (2018), Condições estruturais e funcionais de pontes e viadutos das rodovias federais de Pernambuco. Revista ALCONPAT. 8(1)79-93. http://dx.doi.org/10.21041/ra.v8i1.199
Süssekind, J. C. (1980), “Curso de Concreto: Concreto Armado - Volume I”. Globo, Porto Alegre, Brasil, p. 376.
Toledo, R. L. S. (2011), “Avaliação de vida útil à fadiga em ponte mista aço-concreto considerando o espectro de veículos reais”, Trabalho de Conclusão de Curso em Engenharia, Universidade Federal do Rio de Janeiro, Rio de Janeiro.
Yadav, I. N., Thapa, K. B. (2020), Fatigue damage model of concrete materials. Theoretical and Applied Fracture Mechanics. 108:102578. https://doi.org/10.1016/j.tafmec.2020.102578

