| Revisão | https://doi.org/10.21041/ra.v10i2.478 |
Modelando a corrosão da armadura e estado limite de deterioração
Rebar corrosion modelling and deterioration limit state
Modelado de la corrosión de la armadura y estado límite de deterioro
1 International Centre for Numerical Methods in Engineering (CIMNE), Spain.
*Contact author: candrade@cimne.upc.edu
Recepção: 08 de dezembro de 2019.
Aceitação: 09 de abril de 2020.
Publicação: 30 de abril de 2020.
| Citar como: Andrade, C. (2020), "Modelando a corrosão da armadura e estado limite de deterioração", Revista ALCONPAT, 10(2), pp. 165 – 179, DOI: https://doi.org/10.21041/ra.v10i2.478 |
Resumo
No presente trabalho são apresentadas as limitações dos modelos de iniciação da corrosão com indicações para superá-los. O projeto de durabilidade baseado no desempenho é atualmente uma tendência considerada no Model Code fib (MC2010). No entanto, ainda estamos longe de prever com precisão o desempenho de uma estrutura em um ambiente específico, apesar dos requisitos baseados em desempenho serem introduzidos nas especificações concretas de grandes infraestruturas que exigem 100 anos ou mais de vida útil. Também são comentados o processo de despassivação e o período de propagação com considerações sobre seu tratamento probabilístico. Propõe-se considerar o início da corrosão como um "estado limite de deterioração ou iniciação" (DLS ou ILS). Um exemplo de cálculo é o tempo de corrosão induzida por fissuras no cobrimento.
Palavras-chave:
concreto,
cloretos,
carbonatação,
corrosão,
confiabilidade.
Abstract
In present work the limitations of the models of corrosion initiation with indications to overcome them, are presented. Performance based design of durability is at present a trend considered in fib Model Code (MC2010). However, we are still far from accurately predicting the performance of a structure in a specific environment, in spite of which performance-based requirements are introduced in the concrete specifications of large infrastructures demanding 100 years or more of service life. Also are commented the depassivation step and the propagation period with considerations on their probabilistic treatment. It is proposed to consider corrosion onset as a “deterioration or initiation Limit State” (DLS or ILS). An example of calculation the time to cover-cracking induced corrosion is included.
Keywords:
concrete,
chlorides,
carbonation,
corrosion,
reliability.
Resumen
En el presente trabajo se analizan las limitaciones de los modelos de iniciación de la corrosión con indicaciones prácticas para superarlas. Es una tendencia mundial el desarrollo de normativa basada en prestaciones como se plasmó en el Código Modelo MC2010 del FIB. Sin embargo, los modelos de predicción todavía adolecen de mucha incertidumbre cuando se aplican a una estructura específica, a pesar de lo cual es creciente el número de especificaciones en grandes infraestructuras que exigen 100 años o más de vida útil. También se comentan la etapa de despasivación y el período de propagación con consideraciones sobre su tratamiento probabilísta. Se propone considerar el inicio de la corrosión como un "estado límite de deterioro o iniciación" (DLS o ILS) con un ejemplo de cálculo.
Palabras clave:
hormigón,
cloruros,
carbonatación,
corrosión,
fiabilidad.
1. Introdução
A previsão da vida útil relacionada à corrosão da armadura é atualmente um assunto em desenvolvimento, porque modelos matemáticos foram publicados (Tuutti, 1982; CONTECVET Manual, 2001; DURACRETE, 1998; MC 2010, 2012; Bakker, 1964) e está aumentando a demanda de vida útil predefinida além de 100 anos nas infraestruturas críticas. Os modelos geralmente se baseiam no pressuposto de que a frente de carbonatação ou o limiar de cloreto penetra por difusão, portanto, a segunda lei de Fick em condições de estado não estacionário é aplicada. No entanto, é preciso enfatizar que não existe um modelo que tenha sido aplicado em estruturas de concreto com mais de 30 anos nem considerado que os cimentos e concretos fabricados há cerca de um século atrás possam ser diferentes dos atuais. Essa falta de verificação a longo prazo é importante para ser lembrada pelos projetistas e consultores, porque frequentemente é encontrada nos contratos internacionais solicitações de 120 ou 150 anos de vida útil, que devem ser consideradas mais um palpite do que um fato. Atualmente, não há uma maneira de distinguir por ensaio um concreto com duração de 100 anos sem corrosão de outro com 120 anos de vida útil. Apesar dessa limitação, é certamente importante estudar ainda mais os ensaios e os modelos relacionados à durabilidade, a fim de, precisamente, melhorar a compreensão atual e preencher as lacunas no conhecimento.
A incerteza na previsão levou à aplicação de análise de risco e conceitos probabilísticos e, portanto, no Model Code 2010 (MC 2010, 2012) são definidas as várias funções de estado limite (LSF) relacionadas à carbonatação, entrada de cloretos, ataque de gelo/degelo, e lixiviação. A consideração das incertezas visa à necessidade de identificar que tipo de estado limite deve ser aplicado aos processos relacionados à durabilidade do concreto e qual a probabilidade de corrosão ou deterioração seria adequada.
No presente trabalho, alguns dos aspectos relacionados às limitações dos modelos de corrosão da armadura e seus aspectos probabilísticos serão comentados, atendendo à sequência típica de: período de iniciação, limite de despassivação e propagação da corrosão, finalizando com algumas considerações sobre o estado limite associado a corrosão.
1.1 Período de iniciação
A carbonatação e a entrada de cloreto são identificadas como as duas principais causas de corrosão da armadura (Tuutti, 1982; CONTECVET Manual, 2001; DURACRETE, 1998; MC 2010, 2012). A carbonatação é um processo no qual sua taxa é quase constante ao longo da vida útil e, em seguida, a lei típica da raiz quadrada pode ser aplicada (ver equação [1]) em que VCO2 é a taxa de carbonatação em condições de referência e xc é a profundidade da carbonatação.
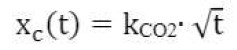 |
[1] |
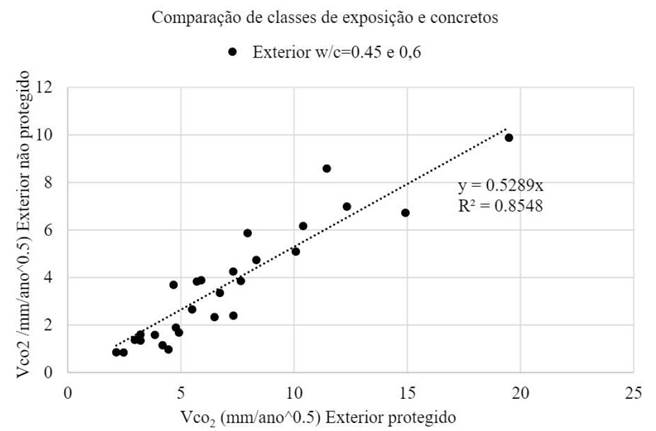
Esse VCO2 depende da composição de concreto escolhida (relação w/c, tipo de cimento e adições minerais) e da influência da execução ou das condições ambientais (umidade relativa média e concentração de CO2). Em geral, a carbonatação progride mais rapidamente quando a UR do ambiente estiver entre 45 e 65%. A profundidade da carbonatação diminui com a UR mais alta (Bakker, 1964) (Fig. 1). A introdução desse efeito na equação [1] é feita pelos modelos disponíveis de várias maneiras. Eles são:
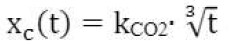
[1’]
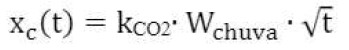
[1’’]
Na Fig. 1 são apresentados os resultados da comparação das taxas de carbonatação (Galan et al. 2010) de ensaios de amostras no clima de Madri durante 4 anos de dois tipos de concretos (com razões w/c de 0,45 e 0,6 e de acordo com, 400 e 300 kg de cimento por m3 de concreto) expostos ao ar livre, protegidos e expostos à chuva. A equação resultante (Galan et al. 2010) nesses ensaios é dada a seguir. Essa relação pode ser diferente em outros climas.
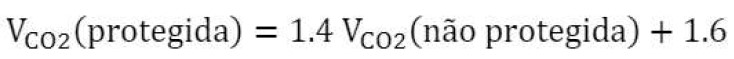 |
[1a] |
Esta equação leva a aplicar um expoente de 0,31 em vez de 0,5 em [1'] e, como indicado na Fig. 1, significa que a taxa de carbonatação exposta à chuva é aproximadamente a metade daquela quando o mesmo concreto é protegido da chuva (Madri clima).
No caso de penetração de cloreto, o cálculo é feito através da expressão denominada “equação da função de erro” (equação [2]) em que C (x, t) é a concentração crítica de cloreto que leva à despassivação dentro do concreto à distância x por um tempo t, Cs é a concentração superficial ou externa de cloreto e Dap é o coeficiente de difusão aparente:
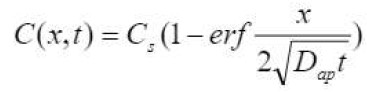 |
[2] |
Com relação à entrada de cloreto, três principais limitações foram identificadas na aplicação da equação [2] (Andrade, 2014):
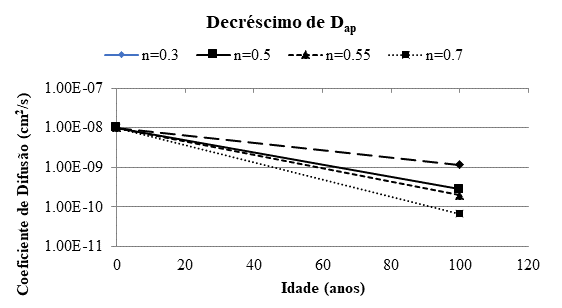
A redução com o tempo do coeficiente de difusão de cloreto é empiricamente abordada (Mangat e Molloy, 1994), considerando que o Dap diminui com o tempo (Fig. 2) seguindo a equação [3] onde n = “fator de envelhecimento”, D0 = coeficiente de difusão no tempo inicial de ensaio t0 (geralmente 28 dias) e ti é o período até quando se supõe que o coeficiente diminua:
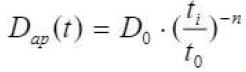 |
[3] |
Esta equação indica que o valor inicial do Dap é alterado para um menor para os cálculos na equação [2]. Embora geralmente aceito, não é indicado como ou quando testar a diminuição e o período de tempo de sua aplicação. Consequentemente, se o período de aplicação é longo, leva a um coeficiente de difusão muito baixo, como mostra a Fig. 2, onde se deduz que, dependendo do fator de envelhecimento (n) considerado, a diminuição pode ser de um ou dois ordens de magnitude. Então, devido às incertezas na extrapolação de um ensaio de curto prazo para longo prazo, a redução deve ser limitada. Uma "boa prática" possível é limitar, dependendo do tipo de cimento, a redução para 1 ano (cimento Portland), 5 anos (cimento com adição de minerais que não sejam escórias ou calcário) ou 10 anos (cimentos com escória como adição de minerais) ou a uma diminuição para limitar a um máximo de uma ordem de magnitude. Finalmente, uma modificação desta equação foi proposta por Gulikers (Tang e Gulikers, 2007) (ver equação [4])
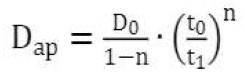 |
[4] |
Ao calcular o Dap por meio dessa expressão, o mesmo resultado é obtido por meio de métodos de elementos finitos ou pelo cálculo direto analítico da equação [2].
Para superar o problema de uma concentração variável na superfície, é viável usar a concentração superficial obtida em um ensaio de difusão natural com duração de 90 dias. Este tempo é longo o suficiente para permitir que a penetração alcance o equilíbrio com a concentração externa de cloreto.
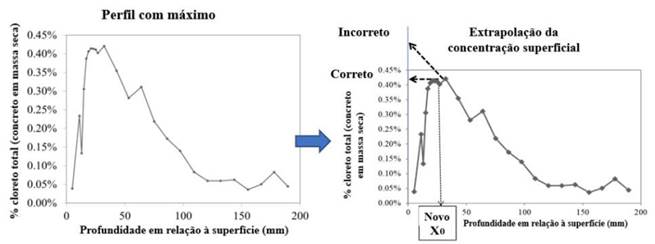
A outra principal limitação está relacionada à consideração de um pico de cloreto que pode ocorrer a poucos milímetros de profundidade, mas não na superfície (Fig. 3 à esquerda) (Andrade, 2015). Esse máximo foi atribuído à “convecção” por absorção capilar, embora pareça mais provável que seja devido à carbonatação da superfície, mas esses motivos não são suficientes para explicar como é possível que a concentração da superfície seja menor que a interna, porque a concentração de cloreto pode até ser quase nula na superfície do concreto na Fig. 3. Deve-se observar também que, para calcular o coeficiente de difusão aparente, a equação Dap, [2] pode ser ajustada neste formato de perfil com o máximo, fornecendo a profundidade “zero” (Fig. 3 à direita) é considerado o da posição máxima (Andrade, 2015), porque o perfil do máximo evolui de acordo com a lei de Fick. Ou seja, o ajuste da equação [2] não deve ser feito extrapolando o máximo de volta à superfície, porque a concentração da superfície seria muito maior que a real. O valor de x0 na figura (distância da superfície à posição máxima) deve ser adicionado ao resultado do cálculo da profundidade do limiar de cloreto (Andrade, 2015) da equação [2]. O que é desconhecido é porque os cloretos tendem a diminuir na superfície e como o máximo se move para dentro, ou seja, a lei de sua evolução com o tempo a longo prazo.
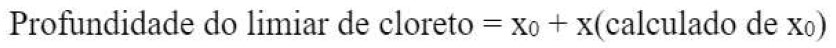
[5]
1.2 Etapa de despassivação
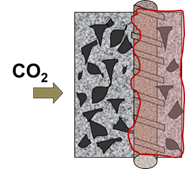
Supõe-se que despassivação significa início da corrosão, mas não é fácil identificar o início da corrosão nas estruturas reais, porque a zona despassivada inicial pode ser tão pequena (Fig. 4) que não é percebida. Nenhum sinal externo pode ser detectado até que Fissuras no cobrimento de concreto ou pontos de corrosão apareçam na superfície. Nenhuma mudança na capacidade de manutenção do concreto é detectada no início da despassivação. Então, a menos que seja feito o monitoramento eletroquímico dos parâmetros de corrosão, não há a possibilidade de detectar o início da corrosão. Mesmo realizando um monitoramento eletroquímico, a identificação da despassivação em condições reais não é uma tarefa fácil devido às mudanças de temperatura e umidade. Essa dificuldade de como detectar e medir o início da despassivação não será abordada no presente trabalho; no entanto, algumas considerações sobre as consequências desse fato serão mencionadas a seguir.

Figura 4.
Pequenos pites de corrosão devido ao ataque de cloretos
Dois aspectos principais serão analisados no processo de despassivação: sua duração e a variabilidade do limiar de cloreto. A duração da despassivação não é um processo instantâneo, mas dura um período de tempo devido à heterogeneidade intrínseca do concreto que torna irregular o limiar frontal.
Para a carbonatação, o limiar de corrosão é atingido quando o valor do pH cai abaixo de 8-9, o que coincide precisamente com a mudança de cor da fenolftaleína, de púrpura para incolor. Devido à presença de agregados, essa frente de carbonatação não é totalmente regular (Thiery, 2007), e consequentemente a superfície da barra será despassivada irregularmente (Fig. 5), o que é mantido até que a frente avance mais fundo. A variabilidade da frente pode ser caracterizada por um valor médio e um desvio padrão (por exemplo, resultando entre 15% e 25% do coeficiente de variação).
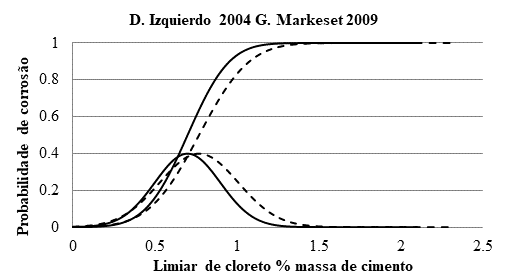
Com relação ao processo de cloreto, a corrosão começa quando certas concentrações críticas de cloreto entram em contato com a superfície do aço. O valor normal considerado em várias normas é de 0,4% em massa de cimento, embora valores tão altos quanto 2-3% possam não desenvolver corrosão em algumas circunstâncias. Então, o limiar não é uma quantidade fixa, mas é um intervalo de valores (Izquierdo et al. 2004; Markeset, 2009) que podem ser tratados estatisticamente. A distribuição de Izquierdo et al. (Izquierdo et al. 2004) é apresentada na Fig. 6. Ele tem um valor médio de Cx = 0,70% (por massa de concreto) com um desvio padrão de ± 0,20%. A distribuição estatística de Markeset (Markeset, 2009) encontrada em estruturas reais é quase semelhante (pontes na Noruega onde os testemunhos extraídos foram perfurados até a barra e a observação de corrosão incipiente foi identificada como o limiar de cloreto).
1.3 Propagação da corrosão
O avanço progressivo da corrosão e a perda no diâmetro da barra e dos óxidos formados induzirão várias consequências estruturais descritas no Manual CONTECVET (2001) (Fig. 7):
(a) Diminuição da seção transversal e da ductilidade da barra.
(b) Fissuras no cobrimento (SLS)
(c) Deterioração da aderência aço/concreto, e
(d) perda de capacidade de carga em relação ao ULS.
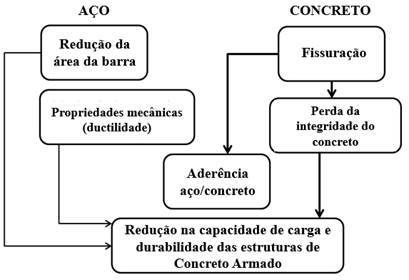
Figura 7.
Consequências da corrosão da armadura (CONTECVET Manual, 2001).
Para calcular o tempo para atingir uma dessas condições de “falha”, é necessário ter um modelo para a evolução da perda de diâmetro da barra. Um modelo foi proposto anos atrás por Andrade et al. (Andrade, 1989; Andrade, 2004) baseado no de Tuutti (Tuutti, 1982). O modelo preliminar foi atualizado mais recentemente (Andrade, 2017), que é mostrado na Fig. 8 como um modelo de propagação bilinear expresso pela equação [5]:
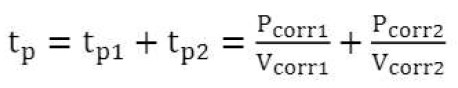 |
[5] |
Onde tp é o período de propagação, Pcorr é a perda no diâmetro da barra ou “corrosão acumulada”, Vcorr é a taxa de corrosão, (0 é o diâmetro inicial, (t é o final após t anos de corrosão. O fator de conversão entre Vcorr e Icorr é: Vcorr (mm / ano) = 0,0116 ( Icorr ((A / cm2). A Fig. 8 apresenta o modelo completo de vida útil (Tuutti, 1982; Andrade, 2017), tendo em vista a possibilidade de que a taxa de corrosão não seja apenas constante (linha A na Fig. 8), mas também esteja apresentando um comportamento em duas etapas: a linha B é o caso quando a corrosão diminui com o tempo e a linha C quando aumenta com o tempo (por exemplo, quando o cobrimento fissura devido à corrosão em ambiente muito úmido). Também mostra que existem várias “condições de falha” (estados limites, como fissuras do cobrimento paralelas às barras), dependendo do grau de corrosão (Andrade, 2017).
A taxa de corrosão depende da porosidade do concreto, do grau de saturação da água e da temperatura de cada ambiente local. Tomando as classes de exposição definidas na norma europeia EN 206, na Tabela 1 são apresentados os valores do Vcorr (considerando linear seu progresso) e o tempo de umidade (Wt) com os desvios padrão esperados (CONTECVET Manual, 2001; DURACRETE, 1998). Também é dado o fator pitting, (.
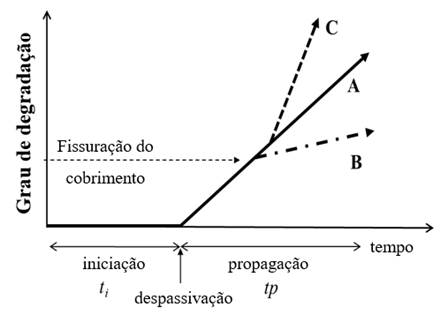
Figura 8.
Modelo de vida útil com as tendências do período de propagação
| Tabela 1. Valores de Vcorr, Wv e fator de pite ( de (2.3) | ||||||||||
| Classes de exposição | Vcorr, a [mm/year] | Wt [-] | α (factor de corrosión local) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Média | Des. Pad. | Distr. | Média | Des. Pad. | Distr. | Média | Des. Pad. | Distr. | ||
| Sem risco de corrosão | 0 | - | D | 0 | - | D | - | - | - | |
| CARBONATION (Totally carbonated) | ||||||||||
| Protegido da chuva | 0.002 | 0.003 | W | 0.5 | 0.12 | N | 2 | 0 | D | |
| No protegido | 0.005 | 0.007 | W | 0.75 | 0.20 | N | 2 | 0 | D | |
| CHLORIDE INITIATED CORROSION | ||||||||||
| Úmido | 0.004 | 0.006 | W | 1 | 0.25 | N | 9.28 | 4.04 | N | |
| Ciclos de secagem por umidade | 0.030 | 0.040 | W | 0.75 | 0.20 | N | 9.28 | 4.04 | N | |
| Spray marinho | 0.030 | 0.040 | W | 0.5 | 0.12 | N | 9.28 | 4.04 | N | |
| Submerso | Nenhuma corrosão ativa ou 0,010 | |||||||||
| Zona das marés | 0.070 | 0.100 | W | 1 | 0.25 | N | 9.28 | 4.04 | N | |
Como o clima pode ser constante ou repetido a cada ano, a corrosão acumulada ou a profundidade de corrosão, Pcorr, (veja a Fig. 9), que é a perda de diâmetro Pcorr, = ((= (0- (i, pode ser, como comentado anteriormente, linear em relação ao tempo (linha A na Fig. 8) ou pode ser considerada uma tendência de duas linhas onde a corrosão diminui com o tempo (Vcorr1> Vcorr2 - linha B) ou aumenta (Vcorr1 <Vcorr2 - linha C).

Figura 9.
Evolução da perda de diâmetro Pcorr com o avanço da frente agressiva.
Se a corrosão é localizada, existe uma dependência da profundidade máxima do pite em relação à corrosão homogênea pela qual é possível estabelecer que (Gonzalez et al, 1995, CONTECVET Manual, 2001):
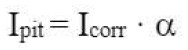 |
[6] | ou | 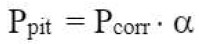 |
[6’] |
Onde α é o “fator de pite” (consulte a tabela 1), responsável pela profundidade máxima do pite. Ou seja, a profundidade máxima do pite é ( vezes mais profunda do que se a corrosão fosse homogênea. O valor médio é α = 10, embora possa variar no caso de ataque de cloreto de 3 a 15 vezes.
2. Estado limite de corrosÃo
A evolução em direção a um projeto de durabilidade baseado em desempenho adicionou o tratamento probabilístico ao cálculo da durabilidade do concreto, conforme desenvolvido no projeto Duracrete (DURACRETE, 1998) e incorporado ao Model Code fib 2010 (MC 2010, 2012) ao tratamento convencional acima. Para o tratamento probabilístico, é definida uma Função de Estado Limite cuja formulação geral é dada a seguir como equação [7]. Uma probabilidade de falha está associada à etapa de despassivação. Portanto:
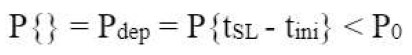 |
[7] |
Onde:
Esta expressão geral é particularizada para cada processo de deterioração. No caso da corrosão da armadura, o estado limite tradicional considerado é o tempo para a despassivação do aço. No entanto, como mencionado, esse estado limite não atende à definição clássica de SLS das normas ISO 16204 (ISO, 2012) e ISO 2394 (ISO, 2015) para o SLS: um estado que corresponde a condições além das quais os requisitos de manutenção especificados para um a estrutura ou seus componentes não são mais satisfeitos, porque quando a corrosão começa, qualquer efeito prejudicial é produzido no nível estrutural e qualquer sinal de dano ou efeito é detectado. Todos os requisitos de manutenção continuam sendo cumpridos durante os primeiros estágios do processo de corrosão. Parece muito mais apropriada a definição de um ILS ou DLS de “estado de limite de deterioração”, dado na norma ISO 13283 (ISO, 2008) ISO,: um estado que corresponde ao início de deterioração significativa de um componente da estrutura.
Uma consequência dessa proposta é que a confiabilidade associada à despassivação pode não ser a de um SLS típico (probabilidades de cerca de 10%), mas deve ser uma que considere as consequências apenas do início da corrosão, que são desprezíveis em geral. Essas consequências foram mencionadas anteriormente (Fig. 7) e, tendo adotado um modelo de propagação da corrosão e valores sugeridos de Vcorr, é possível analisar o efeito do nível de deterioração nas consequências da corrosão e selecionar o nível de confiabilidade mais adequado. Além disso, o projetista deve também verificar o SLS padrão ou o ULS. O procedimento para o projeto (probabilístico completo) deve incluir brevemente:
2.1 Exemplo: verificação da corrosão induzida por fissuras no cobrimento
Com o objetivo de descrever um exemplo, propõe-se que a corrosão induzida por fissuras no cobrimento (paralela às barras e não transversal a elas devido às cargas de flexão) seja considerada como um SLS, porque quando o cobrimento paralelo às barras está em um “estado de condição além do projeto” é alcançado da mesma maneira que quando as fissuras são transversais às barras. O estado limite da corrosão induzida por fissuração pode ser calculado conforme sugerido em MC2010 (MC 2010, 2012) através da equação [8]:
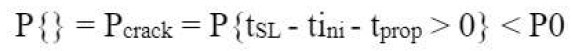 |
[8] |
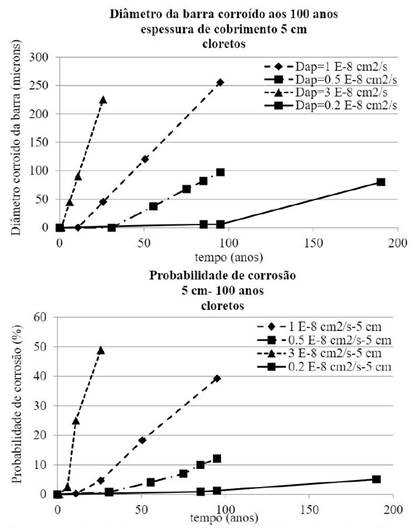
onde: P{} é a probabilidade de que fissuras paralelas sejam produzidas, tSL é a vida útil do projetoVUP [anos], tini é o período de início [anos], tprop é o período de propagação [anos], P0 é a probabilidade de falha alvo. A Fig. 10 mostra, para fins de ilustração do exemplo, a probabilidade de fissuras do cobrimento (para perda de diâmetro da barra de Pcorr = 100 (m (Andrade et al. 2017) associada à fissuras do cobrimento) para vários coeficientes de difusão de cloreto (e taxas de corrosão associado à qualidade do concreto) em um elemento hipotético de 5 cm de cobrimento nominal e uma vida útil de 100 anos.
As deduções mais importantes desses números são que a probabilidade de fissuras no cobrimento não é única, mas varia com a taxa de entrada de cloretos e a taxa de corrosão. Outros parâmetros de entrada, como o fator de envelhecimento ou o coeficiente de variação, também influenciam a probabilidade de atingir Pcorr = 100 (m de perda de diâmetro dentro do período de vida útil. Vale notar que, logicamente, a probabilidade de fissuras no cobrimento ao atingir 100 (m de perda de diâmetro é menor, pois o concreto é de maior qualidade, pois a despassivação será produzida posteriormente. Inversamente, concretos de menor qualidade mostram que uma probabilidade mais alta é encontrada no final da vida útil alvo. Portanto, não é possível estabelecer um valor único como uma probabilidade de falha única, mas dependeria da qualidade do concreto. O fato de que a confiabilidade depende da estrutura é geral e é por isso que o formato semi-probabilístico com “fatores de segurança” gerais é o método normal nas normas existentes. Para atender a um fator de segurança específico, numerosos casos e suas consequências econômicas precisam ser analisados, a fim de selecionar o melhor, oferecendo a maior segurança ao menor custo.
2.2 Verificação do ELU
A metodologia de cálculo do ELU é semelhante à de cálculo para o DLS ou SLS através da determinação da corrosão acumulada, Pcorr, da parte externa da armadura (Fig. 9) e a consideração da correspondente perda geral ou localizada da seção. Então, a partir da seção reduzida da barra e da aderência aço/concreto, a perda na capacidade de carga da seção de concreto poderá será recalculada. Está fora do presente trabalho uma explicação detalhada. Essa explicação detalhada pode ser encontrada no Manual Contecvet (Manual CONTECVET, 2001) e nos relatórios publicados do projeto Duracrete (DURACRETE, 1998).
3. ConclusÕes
Apesar dos progressos realizados no cálculo da vida útil nos últimos 20 anos e da publicação de modelos no MC2010 (MC 2010, 2012), ainda existem inúmeras incertezas e as previsões aos 100 anos não são precisas o suficiente. No presente trabalho, tentou-se propor alguns avanços em relação ao conhecimento atual. Esses são:
4. Agradecimentos
O autor agradece aos fundos fornecidos pelo Ministério da Economia, Indústria e Competitividade da Espanha. Também agradece às frutíferas discussões no comitê TG 8.3 da Comissão 8: Durabilidade da fib, e com os membros do JCSS que lidam com o “capítulo de cargas ambientais” do Model Code Probabilístico.
ReferÊncias
Andrade, C. (2014). 2013 W.R. Whitney Award Lecture: Probabilistic Treatment of the Reinforcement Corrosion. Corrosion, vol. 70, No. 6. pp. 643-651, https://doi.org/10.5006/1049
Andrade, C. (2017), Reliability analysis of corrosion onset: initiation limit state, Journal of Structural Integrity and Maintenance, Pages 200-208, https://doi.org/10.1080/24705314.2017.1388693
Andrade, C., Alonso, C., Gulikers, J., Polder, R., Cigna, R., Vennesland, Ø., Salta, M., Raharinaivo, A., Elsener, B. (2004). "RILEM TC 154-EMC: Electrochemical Techniques for Measuring Metallic Corrosion. Recommendations Test methods for on-site corrosion rate measurement of steel reinforcement in concrete by means of the polarization resistance method." Materials and Structures, 37(273): 623-643.
Andrade, C., Alonso, C., Rodríguez, J. (1989), “Remaining service life of corroding structures”, Proceedings IABSE Symposium on Durability, Lisbonne, pp. 359-363
Andrade, C., Climent, M. A., de Vera, G. (2015), Procedure for calculating the chloride diffusion coefficientand surface concentration from a profile having a maximumbeyond the concrete Surface, Materials and Structures 48:863-869, https://doi.org/10.1617/s11527-015-0543-4
Andrade, C., Díez, J. M., Cruz Alonso, A. (1997) “Mathematical modelling of a concrete surface “skin effect" on Diffusion in chloride contaminated media”. Advances Cement Based Materials, vol.6 (2), 39-44. https://doi.org/10.1016/S1065-7355(97)00002-3
Bakker, R. (1994), “Prediction of service life reinforcement in concrete under different climatic conditions at given cover”, Corrosion and Protection of Steel in Concrete International Conference, Sheffield (U.K.), R.N. Swamy Ed.
Bazant, Z. P. (1979), Physical Model for steel corrosion in concrete sea structures. Theory and application. ASCE Journal of structural Division, June- ST6-p. 14551 (1138-1153)
CONTECVET Manual (2001), A validated user’s manual for assessing the residual life of concrete structures, DG Enterprise, CEC. (The manual can be downloaded from the web site of www.ietcc.csic.es)
DURACRETE (1998), Probabilistic Performance based durability design of concrete structures, Brite EuRam Project 95 - 1347.
Galan I., Andrade C., Mora P., Sanjuan M. A. (2010), Sequestration of CO2 by Concrete Carbonation, Environ. Sci. Technol. 44, 3181-3186.
Gonzalez J.A., Andrade C, Alonso C, Feliu S. (1995), Comparison of rates of general corrosion and maximum pitting penetration on concrete embedded steel reinforcement. Cement and Concrete Research; 25(2): 257-264.
International Organization for Standardization (ISO) (2012), ISO 16204-Durability - Service life designof concrete structures.
International Organization for Standardization (ISO) (2015), ISO 2394- General principles of reliability for structures.
International Organization for Standardization (ISO) (2008), ISO 13283- General principles on the design of structures for durability.
Izquierdo, D., Alonso, C., Andrade, C., Castellote, M. (2004). Potentiostatic determination of chloride threshold values for rebar depassivation Experimental and statistical study, Electrochimica Acta, 49(17-18): 2731-2739, https://doi.org/10.1016/j.electacta.2004.01.034
Mangat, P. S., Molloy, B. T. (1994), Predicting of long term chloride concentration in concrete. Materials and Structures, 27, 338-346. https://doi.org/10.1007/BF02473426
Markeset, G. (2009), Critical chloride content and its influence on service life predictions Critical chloride content and its influence on service life predictions, Materials and Corrosion, 60, No. 8593-596, https://doi.org/10.1002/maco.200905288
MC 2010 (2012), The fib Model Code for Concrete Structures 2010. fib http://www.fib-international.org/fib-model-code-2010 .
Tang, L., Gulikers, J. (2007), On the Mathematics of Time-dependent Apparent Chloride Diffusion Coefficient in Concrete. Cement and Concrete Research, Volume 37, Issue 4, Pages 589-595, https://doi.org/10.1016/j.cemconres.2007.01.006
Thiery, M., Villain, G., Dangla, P., Platret, G. (2007), Investigation of the carbonation front shape on cementitious materials: Effects of the chemical kinetics, Cement and Concrete Research, 37(7), 1047-1058, https://doi.org/10.1016/j.cemconres.2007.04.002
Tuutti, K. (1982), “Corrosion of steel in concrete”, Swedish Cement and Concrete Institute (CBI) nº 4-82. Stockholm.