| Investigación Aplicada | https://doi.org/10.21041/ra.v11i2.454 |
Propuesta de evaluación de daño para dos puentes ubicados en la carretera No. 14 en el estado de Sonora México usando invariante de rigidez como parámetro global de comparación
Damage assessment proposal for two bridges located on Highway No. 14 in the State of Sonora México by using stiffness invariant as global comparison parameter
Proposta de avaliação de danos para duas pontes localizadas na rodovia No. 14 no estado de Sonora, México, usando a variável de rigidez como parâmetro de comparação global
G. Ramos-Torres1 *, H. Navarro-Gómez2, E. Perez-Isidro2, J. Gautherau-Lopez1, I. Palma-Quiroz2
1 Departamento de Ingeniería Civil y Minas, Universidad de Sonora, Hermosillo, México.
2 Instituto de Ciencias Básicas e Ingeniería, Universidad Autónoma del Estado de Hidalgo, México.
* Autor de contacto: calculista@prodigy.net.mx
Recepción: 16 de enero de 2020.
Aceptación: 23 de octubre de 2020.
Publicación: 01 de mayo de 2021.
| Citar como: Ramos-Torres, G., Navarro-Gómez, H., Perez-Isidro, E., Gautherau-Lopez, J., Palma-Quiroz. I. (2021), "Propuesta de evaluación de daño para dos puentes ubicados en la carretera No. 14 en el estado de Sonora México usando invariante de rigidez como parámetro global de comparación", Revista ALCONPAT, 11 (2), pp. 89 – 108, DOI: https://doi.org/10.21041/ra.v11i2.454 |
Resumen
El método de la invariante elástica de rigidez permite obtener la respuesta mecánica de la superestructura de puentes; se basa en la respuesta al impacto de masas conocidas aplicadas al centro del claro para obtener el máximo desplazamiento que define la rigidez puntual, éste se compara con los valores de la curva formada con los invariantes de rigidez, construida a partir de las características de diseño del puente. El método se implementó en dos puentes localizados en la carretera federal No. 14 del Estado de Sonora Mex., con resultados acordes a los daños manifestados. La evaluación es cualitativa a partir de un parámetro global, obtenido en condiciones ambientales en ausencia de viento y a temperatura constante, adecuado para el diagnóstico del estado estructural presente, teniendo limitantes en puentes esviajados.
Palabras clave:
puentes,
superestructura,
impacto,
respuesta mecánica,
rigidez.
Abstract
The elastic rigidity invariant method is used to obtain the mechanical response of the superstructure of simply supported bridges; it is based on the bridge’s response to the impact of known masses applied on mid span to obtain the maximum displacement that defines the point stiffness. This value is compared with the values of the theoretical curve formed with the stiffness invariants, constructed from the design characteristics of the bridge. The method was implemented in two bridges located on federal highway No. 14 of the State of Sonora Mex., with results according to the damage manifested. The evaluation is the result of a global parameter, obtained in environmental conditions in the absence of wind and at a constant temperature, suitable for the diagnosis of the present structural state, having limitations on bridges with screw cross sections.
Keywords:
bridges,
superstructure,
impact,
mechanical response,
stiffness.
Resumo
O método da variável de rigidez elástica permite obter a resposta mecânica da superestrutura da ponte; baseia-se na resposta ao impacto de massas conhecidas aplicadas ao centro do vão (luz) para obter o deslocamento máximo que define a rigidez do ponto, este é comparado com os valores da curva formada com as variáveis de rigidez, construídos a partir do características do projeto estrutural da ponte. O método foi implantado em duas pontes localizadas na rodovia federal nº 14 do Estado de Sonora Mex., com resultados compatíveis com os danos manifestados. A avaliação é qualitativa a partir de um parâmetro global, obtido em condições ambientais na ausência de vento e a temperatura constante, adequado para o diagnóstico do estado estrutural presente, havendo limitações em pontes esconsas.
Palavras-chave:
pontes,
superestrutura,
impacto,
resposta mecânica,
rigidez.
1. IntroducciÓn
A nivel mundial, el diseño y la construcción de puentes está regido por las normas regionales correspondientes e involucra una serie de estudios previos a su diseño y construcción que se soportan en permanentes investigaciones orientadas a la reducción de riesgos de colapso o fallas prematuras; dichas normas incluyen los protocolos de mantenimiento operativo, sin embargo, frecuentemente se presentan fallas e incluso colapsos. Una muestra de 384 puentes colapsados a nivel mundial en el período de 1944 a 2004, reveló que el 28% colapsó por causas naturales, el 21% por errores de diseño, un 18% por impacto, 10% por sobrecarga, 10% por errores humanos, 10% por causas desconocidas, 2% por corrosión y un 1% por vandalismo (Imhof, 2004). La mayor dificultad que se tiene en la inspección de estructuras de puentes es obtener un índice de daño para la toma de decisiones de mantenimiento, reparación o reemplazo.
Un resumen sobre algunos métodos para obtener respuesta mecánica en puentes se presenta enseguida: Para rangos no lineales, se propuso el método de la rótula plástica dinámica; se trata de obtener la curva modal de carga-deformación a partir de un modelo de un grado de libertad. La estructura es sometida a la aceleración de un sismo determinado hasta obtener la respuesta máxima que se presenta en el momento en que se alcanza la plastificación de una rótula previamente propuesta convirtiéndose el sistema en un mecanismo.
Este método simplificado permite visualizar la demanda de ductilidad de la estructura (E. Maldonado, et al. 1998). Mediante métodos numéricos se puede obtener un factor de amplificación que considera los efectos dinámicos aplicable a los elementos mecánicos de diseño de puentes continuos, considerando vigas flexibles y cargas móviles amortiguadas por la suspensión de los camiones tipos analizados. La ecuación de movimiento del puente se asume en vibración forzada por la ecuación de movimiento del camión de prueba que tiene un punto de aplicación de carga por eje, la viga se idealiza como una serie de masas concentradas en intervalos discretos uniformemente distribuidos en su longitud total y los efectos de la carga del camión se computan en el eje frontal; este procedimiento permite obtener un factor de impacto para la carga móvil también conocido como factor de amplificación dinámico, que resulta de las curvas de desplazamiento generadas tanto para carga estática como para carga dinámica.
El procedimiento permite incluir un factor de fricción por participación de la suspensión del camión analizado (N. Munirudrappa et al. 1999). El método de las funciones de respuesta en frecuencias consiste en la obtención de una matriz característica de la estructura, que es función de la masa, del amortiguamiento y de su rigidez. Se obtiene de invertir la matriz de cofactores del vector de funciones de frecuencias de las transformadas de Fourier de la ecuación de movimiento y es conocida como matriz de funciones de respuesta en frecuencias. Esta matriz posee solo las propiedades de la estructura y es independiente de la excitación por lo que cualquier cambio que se genere en ella es debido a cambios en la constitución de la estructura. Si se requiere conocer la matriz de funciones de respuesta en frecuencias, se deben conocer los vectores de desplazamientos y sus fuerzas de excitación en términos de sus transformadas de Fourier. Se puede resumir que es un método complejo, pues requiere de una cantidad mucho mayor de sensores y de un gran procesamiento numérico que acople los efectos locales y globales en comparación con el método de análisis modal.
El método de análisis de sensibilidad consiste en obtener un factor de sensibilidad que equivale al cociente entre la razón de cambio de la frecuencia y la razón de cambio en la rigidez. Este método ayuda a seleccionar los parámetros de mayor impacto en la respuesta y descartar los posibles errores en la instrumentación experimental, de tal forma que permite escoger los valores más significativos o de mayor impacto y a visualizar los elementos estructurales de mayor contribución a los efectos dinámicos, con lo que es posible determinar con buena precisión los puntos donde se deben colocar los sensores para estudios experimentales. Un grupo de métodos experimentales que clasifica a los métodos de simulación numérica, donde se pueden utilizar métodos numéricos como Runge-Kutta, Euler, etc., que resuelven las ecuaciones diferenciales de movimiento a partir del Jacobiano del cociente entre la razón de cambio de las fuerzas y la razón de cambio de los desplazamientos cuyas soluciones reales deben ser negativas para garantizar la estabilidad del método y su integración en el tiempo. En definitiva, el método de elementos finitos es el más usado para resolver las ecuaciones de movimiento, pues utiliza la discretización y la interpolación usando funciones de forma compatibles con los esfuerzos y las deformaciones, considerando el equilibrio interno, el equilibrio en la frontera y la compatibilidad de deformaciones de los elementos discretos que se resuelven por integración directa y ensambladas en sistemas lineales de ecuaciones siempre que las ecuaciones diferenciales sean ordinarias (Carrión F. J. et al. 1999). Un modelo para conocer los efectos de la temperatura comparado con los efectos del daño en el cambio de la frecuencia natural de puentes de un claro, utilizando modelos de elementos finitos para vigas cajón y vigas pretensadas tipo ASHHTO; la conclusión del trabajo indica que los cambios en la frecuencia de la superestructura de un puente de un claro debido a los efectos térmicos, son similares a los efectos del daño acumulado durante un período largo de tiempo debido al ablandamiento temporal (Balmes Etienne et al., 2005).
Se realizó un estudio instrumentando dos puentes de losas y trabes presforzadas, ambos de dos claros independientes; la captura se realizó mediante sensores de aceleración, que con métodos numéricos permitieron conocer los espectros de velocidades y de desplazamientos. Así mismo, con un adecuado filtrado de frecuencias, se logró separar los efectos estáticos y dinámicos del espectro obtenido; la valoración de los resultados indica que los factores de impacto obtenidos mediante el cociente entre el efecto dinámico de la carga y el efecto estático de la misma, bajo ciertas condiciones de masa y velocidad del vehículo de prueba superan a los establecidos en los códigos de diseño regionales (Valdez J. et al. 2008). Un análisis comparativo para obtener la respuesta dinámica de un puente de concreto reforzado que se ubicaba en Italia utilizando un modelo de elementos finitos con elementos tipo Shell y la excitación de un camión tipo a diferentes velocidades.
El análisis teórico se realizó asumiendo la inexistencia del agrietamiento para ignorar la contribución del acero de refuerzo en la estimación de la rigidez. Los resultados obtenidos en el análisis indicaron que con un camión no fue posible obtener los parámetros dinámicos básicos por lo que se usó un convoy continuo de camiones, ofreciendo resultados más acordes con la realidad; el contraste se realizó con los datos obtenidos de la aplicación en sitio de excitación mediante un vibrador eléctrico colocado al cuarto del claro del puente y colocando una serie de 17 sensores de aceleración para obtener la respuesta en tiempo real. Los resultados obtenidos en el análisis presentaron errores desde el 1% hasta el 46% comparados con las frecuencias obtenidas en sitio, siendo la frecuencia a torsión la de menor error y la del cuarto modo a flexión la de mayor error (Veles H. et al 2011). Una metodología para determinar el deterioro por fatiga de la superestructura de puentes de concreto reforzado, utilizando las técnicas de Montecarlo; el método estima probabilísticamente de acuerdo con los datos estadísticos el número de ciclos de carga y su repercusión en el nivel de esfuerzos conforme a los modelos de daño más populares que permiten dar un estimado del tamaño de grieta. Este método es especulativo y puede ser aplicado con relativa facilidad si se conocen las estadísticas de operación del puente bajo análisis, sin embargo, como se presenta, no incluye factores como cargas extraordinarias o sismos y efectos de corrosión entre otros, (Crespo E. et. al. 2013).
Los resultados de la aplicación del método de vibraciones ambientales (cociente espectral) aplicadas a la instrumentación de un puente postensado que les permitió evaluar el estado presente de la superestructura, los resultados de la instrumentación fueron comparados con los resultados del modelo estructural elaborado en un software comercial. (Viviescas Al. et al. 2017).
2. Metodología
De la infraestructura de puentes en carreteras federales en México, el 57% están construidos de concreto reforzado, seguido por el 28% construidos de concreto presforzados, un 7% están construidos en acero y concreto, un 6% en acero estructural, el 1% en mampostería y un 1% en sistema tridilosa (IMT-2014). Acorde a la estadística del Instituto Mexicano del Transporte, el mayor número de puentes está construido de concreto reforzado, por lo que en esta investigación se estudian dos puentes de concreto reforzado, uno a base de losas sólidas y otro construido en trabes y losas con diafragmas de concreto reforzado.
El presente trabajo consiste en la aplicación de una metodología que utiliza parámetros globales; incluye la rigidez puntual real presente de la estructura, que se obtiene a partir de mediciones de campo sobre la estructura real; el valor obtenido, se compara con el valor de rigidez obtenido de los parámetros de diseño del puente que resultan de la función del invariante de rigidez; el cociente entre dichos valores corresponde al residual de capacidad de la estructura permitiendo obtener un índice de daño.
2.1. Conceptos generales.
El comportamiento mecánico de una estructura bajo cargas de servicio depende del nivel de esfuerzos alcanzado y del número de repeticiones o de ciclos de carga; factores como el deterioro, la corrosión, la fatiga y/o el incremento en el nivel de cargas de servicio, puede generar daño permanente que modifiquen las condiciones de su respuesta mecánica. Las consideraciones en el diseño para el desempeño de una estructura contemplan un comportamiento mecánico lineal elástico y se considera saludable mientras que se conserve. Cuando el daño acumulado modifica su comportamiento da inicio el comportamiento no lineal donde la proporción entre los desplazamientos y las fuerzas aplicadas deja de ser constante; es bajo este principio básico que el método propuesto ofrece información del estado presente de la estructura.
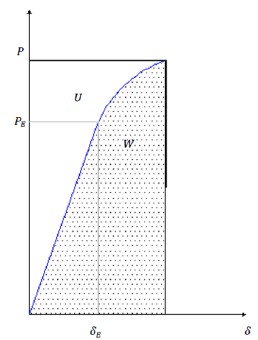
La figura 1 presenta el comportamiento mecánico de un sistema estructural bajo carga monotónica con incremento gradual de carga; primeramente, se aprecia una línea recta que inicia en el origen y alcanza la coordenada(δE, PE), correspondiendo (δE) al desplazamiento hasta el límite elástico lineal y (PE) a la carga en el mismo límite; la parte curvada indica que el sistema estructural tiene un comportamiento no lineal.
El método propuesto considera que si se aplican tres cargas puntuales crecientes se obtiene una gráfica carga-desplazamiento que describe un comportamiento mecánico muy parecido al real; a partir de los incrementos de cargas aplicados, uniendo las coordenadas de los tres puntos se obtiene dos líneas que poseen la misma pendiente si se trabaja en rango lineal o secantes a la curva esfuerzo deformación real de la estructura si el trabajo es en rango no lineal; si los incrementos de cargas son pequeños, las áreas superior e inferior de la curva real son muy parecidas a las áreas superior e inferior de la gráficas de las líneas obtenidas, reduciéndose el error del método. Las áreas descritas permiten obtener una forma de medir el daño.
 |
||||
| Figura 1. Relación carga desplazamiento | ||||
2.2. Evaluación del daño.
La figura 1 está dividida en dos regiones, una inferior cuya área corresponde al trabajo W que se produjo durante el proceso de carga y una superior cuya área corresponde a la energía de deformación U almacenada por la estructura, que le permite recuperar íntegra o parcialmente su forma original si se retira la carga. Cuando el comportamiento mecánico de la estructura es lineal-elástico, el trabajo y la energía de deformación poseen la misma magnitud, lo que implica que la estructura puede recuperar su configuración original si se retiran las cargas; si el comportamiento es no lineal, los valores del trabajo realizado y de la energía de deformación almacenada son diferentes, lo que implica que, al retirar la carga, la estructura recuperará parcialmente su configuración.
Despreciando la energía generada en forma de calor, si la estructura posee comportamiento no lineal, la energía de deformación almacenada es menor al trabajo realizado por el sistema; esta consideración es aplicable en estructuras de concreto reforzado.
Existen algunas expresiones semi empíricas para evaluar el daño en estructuras de concreto reforzado obtenidas de pruebas experimentales; una de las expresiones que permite obtener un índice de daño considerando la pendiente de la parte elástica de la curva de descarga, está definida por la siguiente expresión:
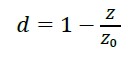 |
(1) |
Donde d es equivalente a un índice de daño, Z corresponde a la pendiente de la parte elástica de la rama de descarga y Z0 es el valor de la pendiente de la rama elástica inicial (Perdomo M. E. et al, 2006). Para comportamiento elástico la expresión tiene un valor nulo y para comportamiento inelástico cercano a la falla el valor es próximo a la unidad. Con esta expresión se puede obtener una curva de restitución de la energía para los elementos de prueba y se consigue el índice de daño que se genera previo a la falla, la dificultad de su uso conlleva la realización de pruebas experimentales para cada tipo de elemento estructural
Acorde con la propuesta del presente trabajo, la deformación real es obtenida de la doble integración del espectro aceleración-tiempo que resulta del impacto aplicado a la estructura real con masas y alturas en caída libre conocidas, considerando la máxima amplitud del desplazamiento para los cálculos.
Conocidas la masas, la altura en caída libre y los desplazamientos máximos, se construye la gráfica energía cinética vs. desplazamiento, identificándose la zona superior de la curva con área Asup, análoga a la densidad de energía de deformación U y la región inferior con área Ainf, análoga a la densidad de trabajo realizado W cuyo cociente ∆k es considerado como una medida de daño, basado en el cambio energético por disminución de la rigidez del sistema por efectos del daño y es aplicable a la mayor carga de prueba.
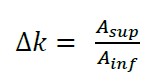 |
(2) |
2.3. Invariante elástica de rigidez.
Está formado con los valores de rigidez por debajo del límite de proporcionalidad a lo largo de la longitud de un elemento estructural. En (3) K, corresponde al valor de rigidez teórica de diseño, F corresponde a la fuerza aplicada y δ es el desplazamiento resultante.
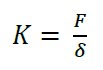 |
(3) |
Si se aplica el principio de trabajo virtual y considerando sólo la contribución del momento flector, la expresión para la rigidez en un punto corresponde a (4).
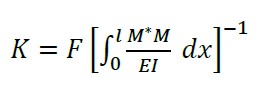 |
(4) |
Si se conserva el valor de la fuerza F constante a lo largo de cada punto de la estructura, se obtiene la curva de rigidez y tiene el carácter de invariante en cada punto bajo el límite de proporcionalidad.
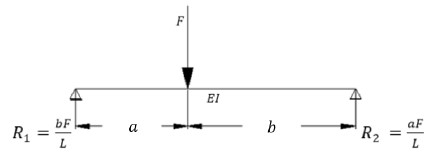
Conforme a la figura 2, si F es aplicada en la coordenada X = a, se requiere determinar la flecha δ y la rigidez K(a).
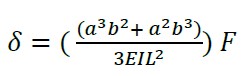 |
(5) |
 |
||||
| Figura 2. Relación carga desplazamiento | ||||
Conocido el desplazamiento se obtiene la rigidez en la coordenada x = a; considerando b = L - a, donde (6) es el invariante de rigidez que se aplica para vigas y (7) invariante para losas sólidas.
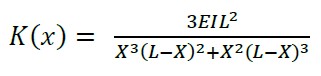 |
(6) |
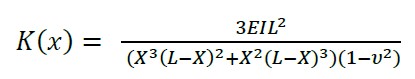 |
(7) |
2.4. Medición de la rigidez puntual real.
La rigidez puntual real se obtiene con el desplazamiento máximo que se produce al someter la superestructura a cargas de impacto aplicadas al centro del claro; para la excitaciòn se utilizan pequeñas masas que modifican mìnimamente los paràmetros dinàmicos de la estructura. Para calcular la fuerza de impacto FR, se recurre a las expresiones fundamentales de la mecánica que se describen en seguida:
 |
(8) |
g = aceleración de la gravedad
h= altura de la caida
Ya que el impacto se realiza en un medio deformable, la magnitud de la fuerza depende de la rigidez de reacción; (9) corresponde a la energía cinética en el momento del impacto.
 |
(9) |
m=masa.
De la gráfica energía cinética-desplazamiento, como ya se mencionó, el área superior de la curva Asup, es análoga a la energía de deformación (U)y el área inferior Ainf, es análoga al trabajo realizado (W), por lo que ∆k corresponde a un factor de rigidez residual, que con valor unitario indica salud estructural y todo valor inferior a la unidad, indica daño permanente del sistema estructural. El factor de rigidez residual ∆k (2) es aplicable a estructuras de concreto reforzado; corresponde al incremento del agrietamiento de la sección transversal, debido a la fluencia del acero de refuerzo por la acumulación del daño, que se refleja en la disminución del área de compresión ya que el agrietamiento a medida que el acero recibe mayor deformación, crece en la zona de tensión y por ende, se reduce el momento de inercia de la sección transversal, expresada por ID para su consideración dentro del método (10). Para conocer el valor de la rigidez real presente, se requiere obtener la fuerza efectiva cuando la energía cinética es nula en el instante del máximo desplazamiento. El valor de la fuerza real para cada grupo de impactos se obtiene del uso de (11) considerando la carga de impacto aplicada al centro del claro.
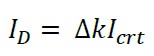 |
(10) |
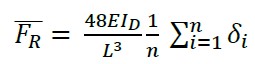 |
(11) |
Con (12), se obtiene la rigidez real presente KR; FR¯ corresponde a la fuerza promedio efectiva de impacto y FR¯ al promedio de los desplazamientos medidos en campo para cada masa.
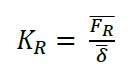 |
(12) |
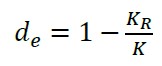 |
(13) |
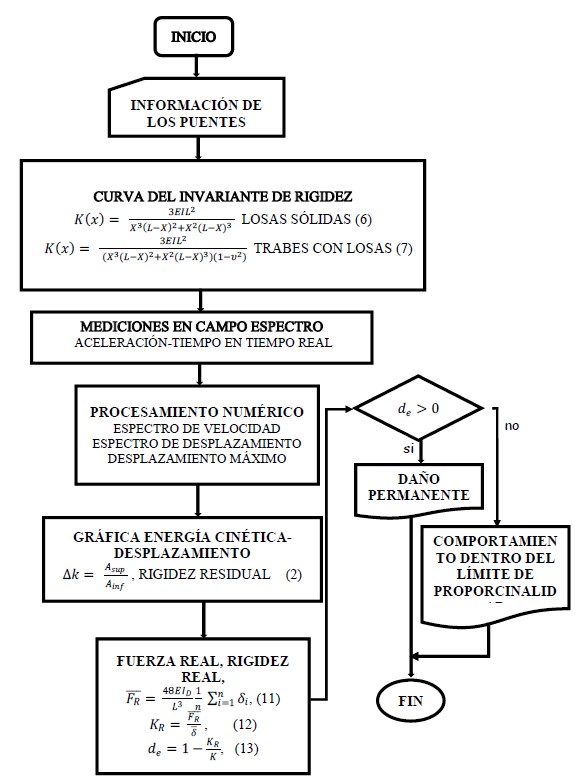
En (13), de se considera un índice de daño y es una medida de la degradación o disminución de la rigidez, en estructuras sanas el valor es nulo, para el colapso es cercano a la unidad y depende de las caracterìsticas de cada estructura. En el método propuesto, la precarga del sistema corresponde a la carga permanente de la estructura, que puede ser del orden de hasta un 85% de la capacidad total de la misma, esto permite utilizar pequeños incrementos de carga para obtener deformaciones en zonas avanzadas de la envolvente de la curva esfuerzo deformación de histéresis. La figura 3 muestra el diagrama de flujo de la metodología usada para los casos de estudio; en primer término, es necesario contar con los planos estructurales de proyecto. Para las mediciones en campo, se utiliza un sistemas de masas que durante el impacto se acoplan al movimiento de la estructura para evitar el rebote, de preferencia, la cantidad de masa para cada grupo de pruebas debe tener valores proporcionales, a fin de facilitar los cálculos correspondientes. Es muy importante que en la elección de las masas de prueba, la aceleración de respuesta de la estructura esté al menos un 20% por debajo del límite máximo de aceleración del sensor y que los valores de aceleración para cada distinta masa, tengan suficiente discriminación para el procesamiento numérico. El resto de las actividades se presentan en la misma figura.
 |
||||
| Figura 3. Diagrama de flujo, Método del invariante de rigidez. | ||||
3. Casos de estudio
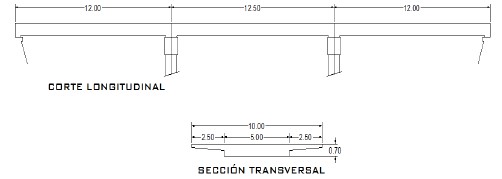
Los puentes instrumentados se localizan en la carretera federal 14, Hermosillo-Moctezuma, en el estado de Sonora, Mex.; uno de los puentes lleva el nombre de “El Testarazo” figura 4, que se localiza en el km 23+900. El puente tiene una superestructura a base de tres losas de concreto reforzado, simplemente apoyadas sobre estribos constituidos por muros de concreto reforzado. El otro puente instrumentado tiene por nombre “El Gavilán” figura 5; la super estructura está formada por un sistema de vigas, losas y diafragmas de concreto reforzado, con sección sesgada a 48° de su dirección transversal, ubicado en el Km 60+100 de la misma carretera.
3.1. Información de los casos de estudio.
 |
||||
| Figura 4. Geometría superestructura puente “Testarazo” (Acot. m). | ||||
 |
||||
| Figura 5. Geometría superestructura puente “El Gavilán” (Acot. m). | ||||
Las propiedades geométricas de las secciones transversales se obtuvieron bajo el criterio de la sección transformada, y los datos de proyecto fueron obtenidos del Proyecto Tipo de Elementos de Concreto Reforzado, Parte I, publicado por la extinta SAHOP.
| Tabla 1. Propiedades geométricas sección transformada de los puentes (m). | ||||||||||||||
| Puente | bw | hf | bf | n | As(m2) | d | kd | Icrt(m4) | A(m2) | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Testarazo | 5.2 | 0.30 | 10.0 | 8.796 | 0.035 | 0.645 | 0.1858 | 0.1108 | 2.95 | |||||
| El Gavilán | 1.08 | 0.18 | 7.5 | 8.796 | 0.0386 | 2.182 | 0.481 | 1.199 | 2.89 | |||||
Para el puente “El Testarazo” EI = 2,595MN - m² (para le rigidez de loza sòlida); para el puente El Gavilan EI = 28,082 MN - m² (para la rigidez de viga). Con estos valores se obtuvo la curva de rigidez. En ambos casos solo se consideran los efectos de flexión. El valor del módulo de elasticidad del concreto se consideró de E = 23,414 Mpa, basado en la expresión E = 15100 √(ƒc')(Kg/cm2).
3.2. Curva de la invariante de rigidez.
Las figuras 6 y 7, muestran las gráficas de los cofactores correspondientes a los invariantes de rigidez para los puentes El Testarazo y El Gavilán, respectivamente, obtenidos de (4) para el puente El Gavilán y de (5) para El Testarazo. Los valores de rigidez de proyecto KE al centro de los claros de la superestructura de los puentes en estudio se presentan en la tabla 2; dichos valores resultan del producto de los cofactores ilustrados en las figuras 6 y 7 con los respectivos valores de EI para cada puente.
| Tabla 2. Valores De rigidez bajo el límite de proporcionalidad. | ||||||||||||||
| Puente | “El Testarazo” | “El Gavilán” | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| KE(MN/m) | 66.432 | 41.237 | ||||||||||||
 |
||||
| Figura 6. Cofactor de rigidez puente “El Testarazo” | ||||
 |
||||
| Figura 7. Cofactor de rigidez puente “El Gavilán” | ||||
3.3. Procedimiento para obtener la rigidez real de la estructura.
Las mediciones en campo se hicieron usando una estructura de elevación y descarga de las masas de excitación, el equipo consiste en un esqueleto cuadrúpedo que permite elevar las masas mediante un winche con capacidad para 2250 N; el mecanismo de sujeción de los contenedores está formado por un electroimán de 6 KN de capacidad que permite engarzar la masa de excitación mediante gancho de seguridad con un grado de libertad a la torsión, (fig. 8).
 |
||||
| Figura 8. Aspecto general del equipo de prueba de campo. | ||||
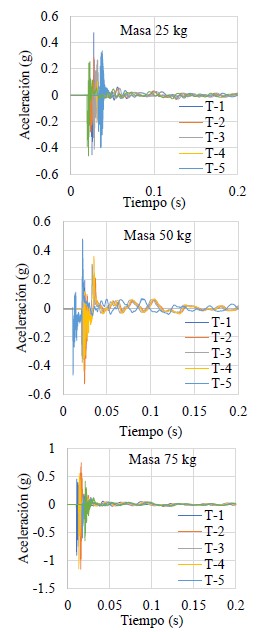
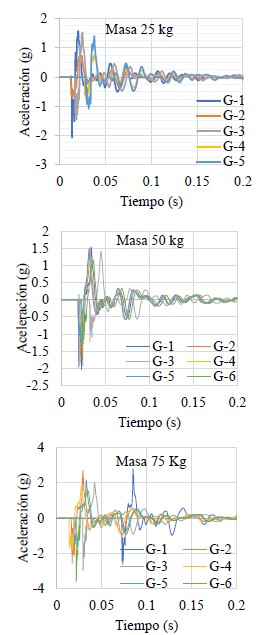
Se usaron contenedores de arena, con comportamiento plástico durante el impacto, para evitar el rebote; se fabricaron tres costales de 25, 50 y 75kg de capacidad, que se llenaron hasta alcanzar la masa de prueba; el impacto se logró elevando los costales a una altura promedio de 1.50m, posteriormente, se interrumpió el flujo eléctrico del electroimán que los sujetaba para soltarlos y producir el impacto en la superficie de rodamiento del puente; el resto del equipo consiste en un sensor de aceleración de baja frecuencia (0.2 Hz), con una sensibilidad de 500 mV/g , colocado al centro del claro que permitió obtener la respuesta del puente en tiempo real , además, una tarjeta de captura de 4 canales para recepción de 0 a 25 khz; la tarjeta permitió la captura de señales analógicas producidas por el sensor durante las mediciones. La tarjeta de captura se colocó sobre un chasis con capacidad para ocho tarjetas 11-30 V de 15 W, para operar de -40º a 70º C comunicado al puerto USB de la computadora portadora del software para procesar la señal analógica donde se obtuvieron los espectros de respuesta aceleración-tiempo de la estructura; las señales analógicas capturadas, se procesaron mediante el Software Labview Signal Express versión 3.0, licencia 501701A-00, que permitió la captura del espectro aceleración-tiempo en una matriz numérica en código ASCII formato TXT, en estado crudo para su procesamiento numérico. Los espectros aceleración-tiempo obtenidos se presentan en las figuras 9, 10 y los desplazamientos se obtuvieron integrando los espectros con los métodos Constant averange acceleration y lineal acceleration method.
3.4. Resultado de las mediciones en campo.
Las figuras 9 y 10 presentan los espectros aceleración tiempo capturados durante las mediciones en campo.
 |
||||
| Figura 9. Espectro aceleración-tiempo real, puente “El Testarazo” | ||||
 |
||||
| Figura 10. Espectro aceleración-tiempo real, puente “El Gavilán” | ||||
Los espectros de aceleración de las figuras 9 y 10, se sometieron a un tratamiento numérico, que consistió, primeramente, en la corrección de la línea base espectral, posteriormente, a la doble integración con los métodos ya descritos para obtener los desplazamientos máximos producidos por el impacto de las masas. En las tablas 3 y 4, se presentan los resultados que incluye la masa de prueba, la altura de caída libre y los desplazamientos obtenidos del procesamiento numérico.
| Tabla 3. Resultado de campo y post proceso numérico puente El Testarazo. . | ||||||||||||||
| MASA (Kg) | ALTURA (m) | DESPLAZAMIENTO (m) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 25 | 1.525 | -2.92927E-05 | ||||||||||||
| 25 | 1.5 | -2.89101E-05 | ||||||||||||
| 25 | 1.484 | -2.84981E-05 | ||||||||||||
| 25 | 1.46 | -2.8037E-05 | ||||||||||||
| 25 | 1.48 | -2.83313E-05 | ||||||||||||
| 25 | 1.55 | -2.98126E-05 | ||||||||||||
| 50 | 1.38 | -5.11297E-05 | ||||||||||||
| 50 | 1.53 | -5.69176E-05 | ||||||||||||
| 50 | 1.55 | -5.76141E-05 | ||||||||||||
| 50 | 1.47 | -5.473E-05 | ||||||||||||
| 50 | 1.548 | -5.7467E-05 | ||||||||||||
| 50 | 1.56 | -5.77907E-05 | ||||||||||||
| 75 | 1.51 | -8.83783E-05 | ||||||||||||
| 75 | 1.49 | -8.69951E-05 | ||||||||||||
| 75 | 1.5 | -8.74758E-05 | ||||||||||||
| 75 | 1.51 | -8.85254E-05 | ||||||||||||
| 75 | 1.49 | -8.7103E-05 | ||||||||||||
| Tabla 4. Resultados de campo y post proceso numérico puente El Gavilán. | ||||||||||||||
| MASA (Kg) | ALTURA (m) | DESPLAZAMIENTO (m) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 25 | 1.54 | -0.000167776 | ||||||||||||
| 25 | 1.52 | -0.000141068 | ||||||||||||
| 25 | 1.55 | -0.00017 | ||||||||||||
| 25 | 1.5 | -0.00013734 | ||||||||||||
| 25 | 1.53 | -0.000163631 | ||||||||||||
| 50 | 1.5 | -0.000260161 | ||||||||||||
| 50 | 1.53 | -0.000268009 | ||||||||||||
| 50 | 1.52 | -0.000266636 | ||||||||||||
| 50 | 1.5 | -0.00026644 | ||||||||||||
| 50 | 1.54 | -0.000273797 | ||||||||||||
| 50 | 1.5 | -0.000258101 | ||||||||||||
| 75 | 1.67 | -0.000491775 | ||||||||||||
| 75 | 1.5 | -0.000440763 | ||||||||||||
| 75 | 1.52 | -0.000448023 | ||||||||||||
| 75 | 1.4 | -0.000412609 | ||||||||||||
| 75 | 1.39 | -0.000408783 | ||||||||||||
| 75 | 1.41 | -0.000414767 | ||||||||||||
3.5. Análisis estadístico de datos obtenidos en campo.
Para conocer la validez de los datos obtenidos en las mediciones realizadas a escala natural de los casos de estudio, se procedió al análisis de varianza o ANOVA; el propósito fundamental es conocer con el análisis bifactorial si los desplazamientos obtenidos son dependientes de la masa y de la altura en caída libre usadas en los ensayos y descartar la posibilidad de que otros factores hallan influido en los resultados. La hipótesis nula H0 asume que los resultados obtenidos son independientes de los factores de prueba; la hipótesis alternativa H1 asume que los resultados son dependientes de al menos uno de los factores, ambas, para un valor de confianza del 95%.
3.5.1. Análisis de varianza para los datos de la tabla 3.
| Tabla 5. Análisis de varianzas bifactorial “El Testarazo”. | ||||||||||||||
| Grados de libertad | Suma de cuadrados | Promedio de los cuadrados | F | Valor crítico de F | f | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Regresión | 2 | 1.04213E-08 | 5.2107E-09 | 2866.0866 | 4.2148E-20 | 0.05146909 | ||||||||
| Residuos | 15 | 2.72706E-11 | 1.818E-12 | |||||||||||
| Total | 17 | 1.04486E-08 | ||||||||||||
Ya que la función de la distribución f < F, se descarta la hipótesis nula H0 y se acepta la hipótesis alternativa; por lo que se afirma que los resultados de desplazamiento obtenidos son dependientes de al menos uno de los factores masa y/o altura de caída libre con un valor de confianza del 95%.
| Tabla 6. Análisis de varianzas (masa-desplazamiento) “El Testarazo”. | ||||||||||||||
| Origen de las variaciones | Suma de cuadrados | Grados de libertad | Promedio de los cuadrados | F | Probabilidad | Valor crítico para F | f | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Entre grupos | 20018.428 | 1 | 20018.4283 | 93.677634 | 5.0095E-11 | 4.1490974 | 0.0039 | |||||||
| Dentro de los grupos | 6838.2352 | 32 | 213.694853 | |||||||||||
| Total | 26856.663 | 33 | ||||||||||||
Al igual que el caso bifactorial, de los valores de la tabla 6, se descarta la hipótesis nula y se acepta la hipótesis alternativa ya que f < F ; se puede afirmar que los desplazamientos obtenidos son dependientes de la masa aplicada con un valor de confianza del 95%.
| Tabla 7. Análisis de varianzas (altura-desplazamiento) “El Testarazo”. | ||||||||||||||
| Origen de las variaciones | Suma de cuadrados | Grados de libertad | Promedio de los cuadrados | F | Probabilidad | Valor crítico para F | f | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Entre grupos | 19.17911772 | 1 | 19.1791 | 20252.1 | 2.061E-46 | 4.149097 | 0.00399 | |||||||
| Dentro de los grupos | 0.03030448 | 32 | 0.00095 | |||||||||||
| Total | 19.2094222 | 33 | ||||||||||||
Como se puede apreciar en la tabla 7, f < F que permite descartar la hipótesis nula, por lo que los desplazamientos obtenidos son dependientes de las alturas de caída de las masas con un valor de confianza del 95%.
3.5.2. Análisis de varianza para los datos de la tabla 4.
| Tabla 8. Análisis de varianzas bifactorial “El Gavilán”. | ||||||||||||||
| Grados de libertad | Suma de cuadrados | Promedio de los cuadrados | F | Valor crítico de F | f | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Regresión | 2 | 2.22636E-07 | 1.1E-07 | 322.93 | 1.93519E-12 | 0.051481683 | ||||||||
| Residuos | 14 | 4.82596E-09 | 3.4E-10 | |||||||||||
| Total | 16 | 2.27462E-07 | ||||||||||||
La tabla 8 presenta los resultados del análisis de varianza; como f < F, se descarta la hipótesis nula H0 y se acepta la hipótesis alternativa; por lo que se afirma que los resultados de desplazamiento obtenidos son dependientes de al menos uno de los factores masa y/o altura de caída libre con un valor de confianza del 95%.
| Tabla 9. Análisis de varianzas (masa-desplazamiento) “El Gavilán”. | ||||||||||||||
| Origen de las variaciones | Suma de cuadrados | Grados de libertad | Promedio de los cuadrados | F | Probabilidad | Valor crítico para F | f | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Entre grupos | 22518.64 | 1 | 22518.6391 | 105.37 | 1E-11 | 4.14909744 | 0.00399430 | |||||||
| Dentro de los grupos | 6838.235 | 32 | 213.694852 | |||||||||||
| Total | 29356.87 | 33 | ||||||||||||
Del análisis de la tabla 9, se descarta la hipótesis nula y se acepta la hipótesis alternativa ya que f < F ; se puede afirmar que los desplazamientos obtenidos son dependientes de la masa aplicada con un valor de confianza del 95%.
| Tabla 10. Análisis de varianzas (altura-desplazamiento) “El Gavilán”. | ||||||||||||||
| Origen de las variaciones | Suma de cuadrados | Grados de libertad | Promedio de los cuadrados | F | Probabilidad | Valor crítico para F | f | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Entre grupos | 19.31294 | 1 | 19.312944 | 9230.5 | 6E-41 | 4.1490974 | 0.0039943 | |||||||
| Dentro de los grupos | 0.066953 | 32 | 0.0020922 | |||||||||||
| Total | 19.3799 | 33 | ||||||||||||
Como se ilustra en la figura 10, f < F; se descartar la hipótesis nula, por lo que los desplazamientos obtenidos son dependientes de las alturas de caída de las masas con un valor de confianza del 95%.
La decisión respecto del análisis de varianza de los datos obtenidos en las mediciones de campo de ambos puentes; se puede afirmar que los resultados de los desplazamientos medidos dependen de las masas usada en el impacto y de sus las alturas de caida libre con un nivel de confianza del 95%, así mismo, se afirma, además, que son los factores de mayor influencia con una probabilidad mayor al 99%.
3.6. Estimación del factor de daño.
Del procesamiento numérico de las señales de las figuras 8 y 9, se obtuvieron los espectros de velocidad y de desplazamiento; conocidas las alturas de caída de las masas, se procedió a la construcción de las gráficas de energía cinética-desplazamiento, utilizando (9) para estimar la energía cinética. Las figuras 11 y 12, muestran las gráficas de energía cinética contra desplazamientos promedios para los dos casos de estudio.
 |
||||
| Figura 11. Relación Energía Cinética-desplazamiento, puente “El Testarazo” | ||||
 |
||||
| Figura 12. Relación Energía Cinética-desplazamiento, puente “El Gavilán” | ||||
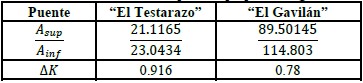
Los valores obtenidos para la reducción por daño del momento de inercia conforme a (10) y (11), se presentan en la tabla11; las áreas corresponden a las superficies superior e inferior de los 3 puntos.
| Tabla 11. Valores de modificación para las propiedades geométricas (I). | ||||||||||||||
 | ||||||||||||||
4. Resultados
Para obtener las fuerzas efectivas que definieron los valores de la rigidez real presente resultado del impacto de las masas de las pruebas de campo, se aplicó (11); en la tabla 12 y se presentan los resultados de las fuerzas y los desplazamientos promedio obtenidos que se usaron para obtener los valores promedio de la rigidez puntual real presente de las superestructuras de los casos de estudio.
| Tabla 12. Valores de fuerzas efectivas y desplazamientos promedio. | ||||||||||||||
 | ||||||||||||||
Con los valores promedio de los desplazamientos y las fuerzas reales obtenidas, aplicando (12) se obtuvieron los valores de la rigidez real de los elementos en estudio. El contraste se realizó con los valores obtenidos del producto de EI por los cofactores de la invariante de rigidez ilustrado en las figuras 6 y 7, respectivamente, para cada puente; los resultados se presentan en la tabla 13.
| Tabla 13. Valores de rigidez real, rigidez de diseño y porcentaje de daño. | ||||||||||||||
 | ||||||||||||||
Valorando el estado de los casos de estudio, es importante aclarar que el índice de daño para estructuras sanas, debe tener valor nulo; conforme a la tabla 14 que resume los resultados obtenidos, se afirma los siguiente: Para el puente “El Testarazo” construido con losas sólidas, el valor del índice de daño es de 12.08%, lo que indica que la estructura posee un 87,9% de su capacidad original; se puede interpretar que, durante la vida de servicio, la superestructura ha perdido rigidez en un 12.08% respecto al estado original, acumulando daño irreversible, tal como se manifiesta en su patología por la flecha excesiva y el agrietamiento transversal alternante al centro del claro. La evidencia que presenta la fig. (10), donde se aprecia que los tres puntos obtenidos para las distintas masas forman dos líneas con distintas pendientes con comportamiento decreciente, demostrando que el estado de la estructura superó el límite de proporcionalidad. El caso del puente “El Gavilán” construido con vigas, losas y diafragmas de concreto reforzado con un esviajamiento de 48°, el índice de daño resultante es del 22.03% lo que indica que posee una capacidad del 77.97% respecto a su capacidad de diseño, que coincide con el agrietamiento y las flechas excesivas existentes en la estructura. Es importante aclarar que la rigidez al desplazamiento vertical depende de la contribución a flexión y a torsión (Deng Kai ,1998); bajo esta consideración, el índice de daño calculado expresado en la tabla 13, incluye la reducción en la rigidez a flexión y a torsión, mas no es posible distinguir que porcentaje le corresponde a cada grado de libertad.
5. Conclusiones
El uso de la invariante de rigidez permitió obtener valores de índice de daño de los casos de estudio acorde a sus condiciones físicas. El procedimiento es relativamente sencillo, sobre todo cuando se cuenta con la información usada en su construcción. La facilidad en el análisis para obtener los datos de contraste, así mismo, la facilidad con las que se obtienen los valores de rigidez real en tiempo presente, son las principales ventajas del método. Las desventajas que se tienen, sobre todo, corresponden a la etapa de medición en campo, ya que se requiere condiciones ambientales de temperatura constante y en ausencia de viento. Otra desventaja es que para puentes esviajados, se requiere un análisis más refinado para la obtención de la invariante de rigidez, ya que con el procedimiento propuesto no se aprecia los porcentajes de reducción que le corresponde tanto a la rigidez por flexión como a la rigidez por torsión.
El método se rige por principios energéticos, puede ser usado en estructuras de concreto reforzado y presforzado con una aproximación aceptable, pues la cuantía de la energía de deformación incluye el área de la región que forma las secantes con la curva real fuerza-desplazamiento y corresponde al error del método; dicho error, es una pequeña porción del trabajo realizado que se le suma a la energía de deformación, por lo que las masas de prueba se deben escoger con incrementos lo más pequeños posible a fin de minimizar el error o en su defecto, estimar el error ajustando logísticamente los tres puntos y obtener el área de los arcos pare ser restados de la energía de deformación y sumados al trabajo realizado. El desarrollo del ajuste por error queda fuera del alcance del presente trabajo.
Otra de las condiciones en el uso del método, consiste en que el peso propio de la estructura, debe ser una parte importante de la carga de servicio por lo que se recomienda para su uso en puentes de losas y trabes.
Referencias
LCPC Balmes, E., Corus, M., Siegert, D. (1998). Modeling thermal effects on bridge dynamic responses, Ecole Centrale Paris/MSSMat, SDTools, balmes@sdtools.com.
Publicación Técnica No. 132 Carrión Viramontes, F. J., Lozano Guzmán, A., Fabela Gallegos, M., Vázquez Vega, D., Romero Navarrete, J. A. (1999). “Evaluación de puentes mediante el análisis de vibraciones ”, Instituto Mexicano del Transporte, , ISSN: 0188-7297. URL: http://www.imt.mx/archivos/Publicaciones/PublicacionTecnica/pt132.pdf
Publicación Técnica No. 379 Crespo Sánchez, S. E., Carrión Viramontes, F., Quintana Rodríguez, J. A., Hernández Guzmán, A., López López, J. A. (2013), “Análisis del deterioro estructural por fatiga y prognosis de un puente típico de concreto utilizando simulación MonteCarlo”, Instituto Mexicano del Transporte, , ISSN: 0188-7297, URL: https://imt.mx/archivos/Publicaciones/PublicacionTecnica/pt379.pdf
Deng, K. (1998), “Dynamic response of certain types of highway bridges to moving vehicles”, Phd. Thesis, The Doctor of Philosophy program in Civil and Environmental Engineering is a joint program with the University of Ottawa administered by The Ottawa-Carleton Lnstitute for Civil Engineering. URL: https://www.collectionscanada.gc.ca/obj/s4/f2/dsk2/ftp02/NQ37062.pdf
Singer, F. L. (1975), “Engineering Mechanics: Statics and Dynamics ”, Third Edition, Harper & Row, New York, I.S.B.N. 968-6034 16-1.
Imhof, D. (2004). Risk assessment of existing bridge structures. (Doctoral thesis) University of Cambridge. https://doi.org/10.17863/CAM.19092
Valdés, J., De la Colina, J. (2008). Análisis de la Amplificación Dinámica de la Carga Viva en Puentes con Base en Pruebas Experimentales. Revista Tecnológica - ESPOL, 21(1), 149 - 156. Recuperado a partir de http://www.rte.espol.edu.ec/index.php/tecnologica/article/view/150
Luthe, R. (1971), “Análisis Estructural”, Representaciones y Servicios de Servicios de Ingeniería, S. A. México.
MIS27 Maldonado, E., Canas, J., Casas, J., Pujades, L. (1998), Respuesta de puentes frente a acciones sísmicas, Monograph Series in Earthquake Engineering, editor A. H. Barbat. , ISBN: 84-89925-23-2, URL: https://www.scipedia.com/public/Maldonado_et_al_2019a
392 Munirudrappa, N., Dhrujavara Iyengar, H. N. (1999), “Dynamic Analysis of Continuous Span Highway bridge”, ISET Journal of Earthquake Technology, No. , 36 (1), 73 - 84. URL: http://home.iitk.ac.in/~vinaykg/Iset392.pdf
Park, R., Paulay, T. (1988), “Estructuras de Concreto Reforzado”, Editorial Limusa, S. A. de C. V. México, D. F., Cuarta reimpresión, I.S.B.N. 968-18-0100-8.
Perdomo, M. E., Castro, L., Picón, R., Marante, M. E., Flórez-López, J. (2006). Modelo de daño para elementos de concreto armado sometidos a corte y flexión. Revista de la Facultad de Ingeniería Universidad Central de Venezuela, 21(4), 23-36. ISSN 0798-4065.
Cuarta colección Secretaría de Asentamientos Humanos y Obras Públicas (1980), “Puentes para Carreteras. Proyectos Tipo de Elementos de Concreto Reforzado. Parte I.”, Diciembre de 1980, México, Editado por SAHOP.
Timoshenko, S., Woinowsky-Krieger, S. (1989), “Theory of plates and Shells”, Second edition, McGRAW-HILL BOOK COMPANY, New York, ISBN 0-07-064779-8.
Vélez Gómez, W. H., Riveros Jerez, C. A. (2011), “Caracterización dinámica en condiciones de excitación natural de puentes de concreto reforzado”, Vector, 6, 36 - 44.
