| Pesquisa Aplicada | https://doi.org/10.21041/ra.v11i2.454 |
Proposta de avaliação de danos para duas pontes localizadas na rodovia No. 14 no estado de Sonora, México, usando a variável de rigidez como parâmetro de comparação global
Damage assessment proposal for two bridges located on Highway No. 14 in the State of Sonora México by using stiffness invariant as global comparison parameter
Propuesta de evaluación de daño para dos puentes ubicados en la carretera No. 14 en el estado de Sonora México usando invariante de rigidez como parámetro global de comparación
G. Ramos-Torres1 *, H. Navarro-Gómez2, E. Perez-Isidro2, J. Gautherau-Lopez1, I. Palma-Quiroz2
1 Departamento de Ingeniería Civil y Minas, Universidad de Sonora, Hermosillo, México.
2 Instituto de Ciencias Básicas e Ingeniería, Universidad Autónoma del Estado de Hidalgo, México.
* Autor de contato: calculista@prodigy.net.mx
Recepção: 16 de janeiro de 2020.
Aceitação: 23 de outubro de 2020.
Publicação: 01 de maio de 2021.
| Citar como: Ramos-Torres, G., Navarro-Gómez, H., Perez-Isidro, E., Gautherau-Lopez, J., Palma-Quiroz. I. (2021), "Proposta de avaliação de danos para duas pontes localizadas na rodovia No. 14 no estado de Sonora, México, usando a variável de rigidez como parâmetro de comparação global", Revista ALCONPAT, 11 (2), pp. 89 – 108, DOI: https://doi.org/10.21041/ra.v11i2.454 |
Resumo
O método da variável de rigidez elástica permite obter a resposta mecânica da superestrutura da ponte; baseia-se na resposta ao impacto de massas conhecidas aplicadas ao centro do vão (luz) para obter o deslocamento máximo que define a rigidez do ponto, este é comparado com os valores da curva formada com as variáveis de rigidez, construídos a partir do características do projeto estrutural da ponte. O método foi implantado em duas pontes localizadas na rodovia federal nº 14 do Estado de Sonora Mex., com resultados compatíveis com os danos manifestados. A avaliação é qualitativa a partir de um parâmetro global, obtido em condições ambientais na ausência de vento e a temperatura constante, adequado para o diagnóstico do estado estrutural presente, havendo limitações em pontes esconsas.
Palavras-chave:
pontes,
superestrutura,
impacto,
resposta mecânica,
rigidez.
Abstract
The elastic rigidity invariant method is used to obtain the mechanical response of the superstructure of simply supported bridges; it is based on the bridge’s response to the impact of known masses applied on mid span to obtain the maximum displacement that defines the point stiffness. This value is compared with the values of the theoretical curve formed with the stiffness invariants, constructed from the design characteristics of the bridge. The method was implemented in two bridges located on federal highway No. 14 of the State of Sonora Mex., with results according to the damage manifested. The evaluation is the result of a global parameter, obtained in environmental conditions in the absence of wind and at a constant temperature, suitable for the diagnosis of the present structural state, having limitations on bridges with screw cross sections.
Keywords:
bridges,
superstructure,
impact,
mechanical response,
stiffness.
Resumen
El método de la invariante elástica de rigidez permite obtener la respuesta mecánica de la superestructura de puentes; se basa en la respuesta al impacto de masas conocidas aplicadas al centro del claro para obtener el máximo desplazamiento que define la rigidez puntual, éste se compara con los valores de la curva formada con los invariantes de rigidez, construida a partir de las características de diseño del puente. El método se implementó en dos puentes localizados en la carretera federal No. 14 del Estado de Sonora Mex., con resultados acordes a los daños manifestados. La evaluación es cualitativa a partir de un parámetro global, obtenido en condiciones ambientales en ausencia de viento y a temperatura constante, adecuado para el diagnóstico del estado estructural presente, teniendo limitantes en puentes esviajados.
Palabras clave:
puentes,
superestructura,
impacto,
respuesta mecánica,
rigidez.
1. IntroduÇÃo
Em todo o mundo, o projeto e construção de pontes é regido pelas normas regionais correspondentes e envolve uma série de estudos anteriores ao seu projeto e construção que são apoiados por pesquisas permanentes destinadas a reduzir o risco de colapso ou falhas prematuras. Esses padrões incluem protocolos de manutenção operacional, no entanto, falhas, danos e até mesmo o colapso ocorrem com frequência. Uma amostra de 384 pontes colapsadas em todo o mundo no período de 1944 a 2004 revelou que 28% desabaram devido a causas naturais, 21% devido a erros de projeto, 18% devido a impacto, 10% devido à sobrecarga, 10% devido a erros construtivos, 10% de causas desconhecidas, 2% por corrosão e 1% por vandalismo (Imhof, 2004). A maior dificuldade na inspeção de estruturas de pontes é obter um índice de dano para a tomada de decisões de manutenção, reparo ou substituição.
Um resumo de alguns métodos de obtenção de resposta mecânica em pontes é apresentado a seguir. Para faixas não lineares, foi proposto o método da rótula plástica dinâmica; trata-se de obter a curva modal de carga-deformação a partir de um modelo com um grau de liberdade. A estrutura é submetida à aceleração de um determinado impacto ou tremor até que seja obtida a resposta máxima, que ocorre no momento em que se atinge a plastificação de uma rótula proposta anteriormente, transformando o sistema em um mecanismo.
Este método simplificado permite visualizar a demanda de ductilidade da estrutura (E. Maldonado, et al. 1998). Por meio de métodos numéricos, pode-se obter um fator de amplificação que considera os efeitos dinâmicos aplicáveis aos elementos de projeto mecânico de pontes contínuas, considerando vigas flexíveis e cargas móveis amortecidas pela suspensão dos trens-tipo analisados. A equação do movimento da ponte é assumida em vibração forçada pela equação do movimento do caminhão de ensaio que possui um ponto de aplicação de carga por eixo, a viga é idealizada como uma série de massas concentradas em intervalos discretos uniformemente distribuídas em seu comprimento total e os efeitos do carregamento do caminhão são calculados no eixo dianteiro; Esse procedimento permite obter um fator de impacto para a carga móvel, também conhecido como fator de amplificação dinâmica, que resulta das curvas de deslocamento geradas tanto para carga estática quanto para carga dinâmica.
O procedimento permite incluir um fator de atrito devido à participação da suspensão do caminhão analisado (N. Munirudrappa et al. 1999). O método das funções de resposta em frequências consiste na obtenção de uma matriz característica da estrutura, que é função da massa, do amortecimento e da sua rigidez. É obtido pela inversão da matriz de cofatores do vetor de funções de frequência das transformadas de Fourier da equação do movimento e é conhecido como matriz de funções de resposta em frequência. Esta matriz possui apenas as propriedades da estrutura e é independente da excitação, portanto qualquer alteração nela gerada deve-se a alterações na constituição da estrutura. Se necessário conhecer a matriz das funções de resposta em frequência, os vetores de deslocamento e suas forças de excitação devem ser conhecidos em termos de suas transformadas de Fourier. Pode-se resumir que é um método complexo, pois requer um número muito maior de sensores e um grande processamento numérico que acopla os efeitos locais e globais em comparação ao método de análise modal.
O método de análise de sensibilidade consiste em obter um fator de sensibilidade equivalente ao quociente entre a taxa de variação da frequência e a taxa de variação da rigidez. Este método ajuda a selecionar os parâmetros com maior impacto na resposta e a descartar possíveis erros na instrumentação experimental, de forma que permite escolher os valores mais significativos ou de maior impacto e visualizar os elementos estruturais com a maior contribuição para os efeitos dinâmicos, com os quais é possível determinar com boa precisão os pontos onde os sensores devem ser colocados para estudos experimentais. Um grupo de métodos experimentais que classifica métodos de simulação numérica, onde podem ser usados métodos numéricos como Runge-Kutta, Euler, etc., que resolvem as equações diferenciais de movimento a partir do Jacobiano do quociente entre a taxa de variação das forças e a taxa de variação dos deslocamentos cujas soluções reais devem ser negativas para garantir a estabilidade do método e sua integração no tempo.
Em suma, o método dos elementos finitos é o mais utilizado para resolver as equações do movimento, pois utiliza discretização e interpolação por meio de funções compatíveis com os esforços e deformações, considerando o equilíbrio interno, o equilíbrio na fronteira e a compatibilidade das deformações dos elementos discretos que são resolvidos por integração direta e montados em sistemas lineares de equações sempre que as equações diferenciais sejam ordinárias (Carrión FJ et al. 1999). Um modelo para conhecer os efeitos da temperatura comparados aos efeitos do dano na mudança da frequência natural das pontes em um vão, utilizando modelos de elementos finitos para vigas em caixão e vigas protendidas tipo ASHHTO; a conclusão do trabalho indica que as mudanças na frequência da superestrutura de uma ponte de um vão devido aos efeitos térmicos, são semelhantes aos efeitos dos danos acumulados durante um longo período de tempo devido ao amortecimento temporal (Balmes Etienne et al., 2005).
Foi realizado um estudo por meio da instrumentação de duas pontes em laje e vigas protendidas, ambas de dois vãos independentes; a captura foi realizada por meio de sensores de aceleração, que com métodos numéricos foi possível conhecer os espectros de velocidades e deslocamentos. Da mesma forma, com uma filtragem de frequência adequada, foi possível separar os efeitos estáticos e dinâmicos do espectro obtido. A avaliação dos resultados indica que os fatores de impacto obtidos por meio do quociente entre o efeito dinâmico da carga e o efeito estático da mesma, sob certas condições de massa e velocidade do veículo de ensaio, superam aqueles estabelecidos nas normas de projeto regionais (Valdez J. et al. 2008). Uma análise comparativa para obter a resposta dinâmica de uma ponte de concreto armado localizada na Itália usando um modelo de elementos finitos com elementos do tipo Shell e a excitação de um caminhão típico em diferentes velocidades.
A análise teórica foi realizada assumindo a inexistência de fissuras para ignorar a contribuição da armadura de aço na estimativa da rigidez. Os resultados obtidos na análise indicaram que com o caminhão não foi possível obter os parâmetros dinâmicos básicos, então foi utilizado um comboio contínuo de caminhões, oferecendo resultados mais condizentes com a realidade; o contraste foi realizado com os dados obtidos da aplicação no local de excitação por meio de um vibrador elétrico colocado no quarto do vão da ponte e colocando uma série de 17 sensores de aceleração para obter a resposta em tempo real.
Os resultados obtidos na análise apresentaram erros de 1% a 46% em relação às frequências obtidas no local, sendo a frequência de torção a de menor erro e a do quarto modo de flexão a de maior erro (Veles H. et al. 2011). Uma metodologia para determinar a deterioração por fadiga da superestrutura de pontes de concreto armado, utilizando técnicas de Montecarlo; o método estima probabilisticamente de acordo com os dados estatísticos o número de ciclos de carga e seu impacto no nível de tensão de acordo com os modelos de dano mais populares que permitem uma estimativa do tamanho da fissura. Este método é especulativo e pode ser aplicado com relativa facilidade se as estatísticas de funcionamento da ponte em análise forem conhecidas, no entanto, conforme apresentado, não inclui fatores como cargas extraordinárias ou terremotos e efeitos de corrosão, entre outros, (Crespo E. et al.. Al. 2013).
Os resultados da aplicação do método de vibrações ambientais (razão espectral) aplicado à instrumentação de uma ponte pós-tensionada permitiu avaliar o estado atual da superestrutura. Os resultados da instrumentação foram comparados com os resultados do modelo estrutural elaborado em um software comercial. (Viviescas Al. Et al. 2017).
2. Metodologia
Da infraestrutura de pontes em rodovias federais no México, 57% são construídas em concreto armado, seguido por 28% construídas em concreto protendido, 7% são construídas em aço e concreto, 6% em aço estrutural, 1% em alvenaria e 1% em sistema de vigas pré-fabricadas (IMT-2014). De acordo com as estatísticas do Instituto Mexicano de Transporte, o maior número de pontes é construído em concreto armado, portanto, nesta pesquisa são estudadas duas pontes de concreto armado, uma constituída de lajes maciças e outra construída sobre vigas e lajes com diafragmas de concreto armado.
O presente trabalho consiste na aplicação de uma metodologia que utiliza parâmetros globais; inclui a rigidez pontual real da estrutura, que é obtida a partir de medições de campo na estrutura real; o valor obtido é comparado com o valor de rigidez obtido a partir dos parâmetros de projeto da ponte que resultam da função variável de rigidez; o quociente entre estes valores corresponde à capacidade residual da estrutura, permitindo obter um índice de dano.
2.1. Conceitos gerais.
O comportamento mecânico de uma estrutura sob cargas de serviço depende do nível de esforços realizados e do número de repetições ou ciclos de carga; fatores como deterioração, corrosão, fadiga e / ou aumento do nível de cargas de serviço podem gerar danos permanentes que modificam as condições de sua resposta mecânica. As considerações de projeto para o desempenho de uma estrutura contemplam o comportamento mecânico linear elástico e é considerada saudável desde que preservada. Quando o dano acumulado modifica seu comportamento, começa o comportamento não linear onde a proporção entre os deslocamentos e as cargas aplicadas não é mais constante; é sob este princípio básico que o método proposto oferece informações sobre o estado atual da estrutura.
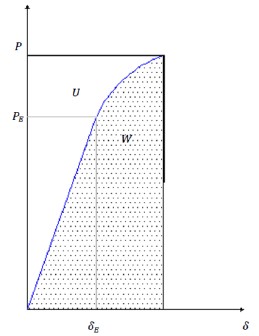
A Figura 1 apresenta o comportamento mecânico de um sistema estrutural sob carga monotônica com aumento gradual da carga; primeiramente, observa-se uma reta que começa na origem e atinge a coordenada δ E , P E , correspondendo δ E ao deslocamento até o limite elástico linear e P E à carga no mesmo limite; a parte curva indica que o sistema estrutural tem um comportamento não linear.
O método proposto considera que se forem aplicadas três cargas pontuais crescentes, obtém-se um gráfico carga-deslocamento que descreve um comportamento mecânico muito semelhante ao real; A partir dos incrementos de carga aplicada, juntando as coordenadas dos três pontos, obtêm-se duas retas que possuem a mesma inclinação se trabalhando em faixa linear ou secante à curva tensão-deformação real da estrutura se o trabalho for em faixa não linear; se os incrementos de carga são pequenos, as áreas superior e inferior da curva real são muito semelhantes às áreas superior e inferior dos gráficos das linhas obtidas, reduzindo o erro do método. As áreas descritas fornecem uma maneira de medir os danos.
 |
||||
| Figura 1. Relação carga deslocamento | ||||
2.2. Avaliação de danos.
A Figura 1 está dividida em duas regiões, uma inferior cuja área corresponde ao trabalho W que foi produzido durante o processo de carregamento e uma superior cuja área corresponde à energia de deformação U armazenada pela estrutura, o que lhe permite recuperar total ou parcialmente sua forma original se a carga for removida. Quando o comportamento mecânico da estrutura é elástico-linear, o trabalho e a energia de deformação têm a mesma magnitude, o que implica que a estrutura pode recuperar sua configuração original se as cargas forem removidas; se o comportamento for não linear, os valores do trabalho realizado e da energia de deformação armazenada são diferentes, o que implica que, quando a carga for retirada, a estrutura recuperará parcialmente sua configuração.
Desconsiderando a energia gerada na forma de calor, se a estrutura tiver comportamento não linear, a energia de deformação armazenada é menor que o trabalho realizado pelo sistema. Esta consideração é aplicável em estruturas de concreto armado.
Existem algumas expressões semi-empíricas para avaliar os danos em estruturas de concreto armado obtidas em ensaios experimentais; uma das expressões que permite obter um índice de danos considerando a inclinação da parte elástica da curva de descarga, é definida pela seguinte expressão:
 |
(1) |
Onde d é equivalente a um índice de dano, Z corresponde à inclinação da parte elástica do ramo de descarga e Z0 é o valor da inclinação do ramo elástico inicial (Perdomo M. E. et al, 2006). Para comportamento elástico, a expressão tem valor nulo e para o comportamento inelástico próximo à falha o valor é próximo da unidade. Com esta expressão, pode-se obter uma curva de restituição de energia para os elementos de ensaio e obter o índice de danos gerado antes da falha, a dificuldade de sua utilização implica a realização de ensaios experimentais para cada tipo de elemento estrutural.
De acordo com a proposta do presente trabalho, a deformação real é obtida a partir da dupla integração do espectro aceleração-tempo que resulta do impacto aplicado à estrutura real com massas e alturas conhecidas em queda livre, considerando a amplitude máxima do deslocamento para os cálculos.
Conhecendo as massas, a altura em queda livre e os deslocamentos máximos, o gráfico da energia cinética vs. deslocamento, identificando a zona superior da curva com área Asup,, análoga à densidade de energia de deformação U e a região inferior com área Ainf, análoga à densidade de trabalho realizado W cujo quociente ∆k é considerado como uma medida de dano, com base no mudança energética devido à diminuição da rigidez do sistema devido a danos e é aplicável à carga de ensaio mais alta.
 |
(2) |
2.3. Variável elástica de rigidez.
É formado com os valores de rigidez abaixo do limite de proporcionalidade ao longo do comprimento de um elemento estrutural. Em (3) K, corresponde ao valor de rigidez teórico de projeto, F corresponde à força aplicada e δ é o deslocamento resultante.
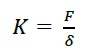 |
(3) |
Se for aplicado o princípio do trabalho virtual e considerando apenas a contribuição do momento fletor, a expressão para a rigidez em um ponto corresponde a (4).
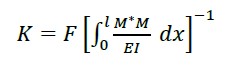 |
(4) |
Se o valor da força F for mantido constante ao longo de cada ponto da estrutura, a curva de rigidez é obtida e tem o caráter de invariante em cada ponto abaixo do limite de proporcionalidade.
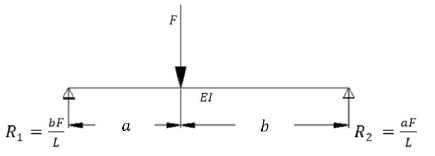
De acordo com a figura 2, se F for aplicado na coordenada X = a, é necessário determinar a flecha δ e a rigidez K (a).
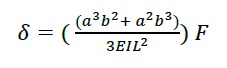 |
(5) |
 |
||||
| Figura 2. Relação carga deslocamento | ||||
Conhecendo o deslocamento, a rigidez é obtida na coordenada x = a; considerando b = L-a, onde (6) é o invariante de rigidez aplicado para vigas e (7) invariante para lajes maciças.
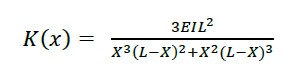 |
(6) |
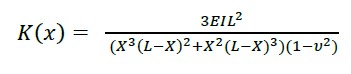 |
(7) |
2.4. Medição da rigidez pontual real.
A rigidez real do ponto é obtida com o deslocamento máximo que ocorre ao submeter a superestrutura a cargas de impacto aplicadas ao centro do vão; para a excitação, são utilizadas pequenas massas que modificam minimamente os parâmetros dinâmicos da estrutura. Para calcular a força de impacto FR, se recorre às expressões fundamentais da mecânica descritas abaixo:
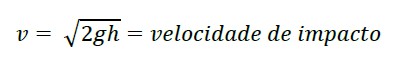 |
(8) |
g = aceleração da gravidade
h= altura de queda
Como o impacto é feito em meio deformável, a magnitude da força depende da rigidez da reação; (9) corresponde à energia cinética no momento do impacto.
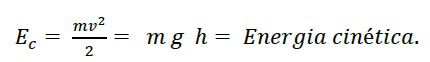 |
(9) |
m = massa
Do gráfico de energia cinética-deslocamento, como já mencionado, a área superior da curva Asup, é análoga à energia de deformação (U) e a área inferior Ainf, é análoga ao trabalho realizado (W), pelo que ∆k corresponde a um fator de rigidez residual, que com um valor unitário indica saúde estrutural e qualquer valor inferior à unidade, indica dano permanente ao sistema estrutural.
O fator de rigidez residual ∆k (2) é aplicável a estruturas de concreto armado; corresponde ao aumento da fissuração da seção transversal, devido à fluência da armadura devido ao acúmulo do dano, o que se reflete na diminuição da área de compressão uma vez que a fissuração, à medida que o aço recebe maior deformação, cresce na zona de tensão e, portanto, o momento de inércia da seção transversal é reduzido, expresso por ID para sua consideração dentro do método (10). Para saber o valor da rigidez real presente, é necessário obter a força efetiva quando a energia cinética é zero no instante do deslocamento máximo. O valor da força real para cada grupo de impactos é obtido a partir da utilização de (11) considerando a carga de impacto aplicada ao centro do vão.
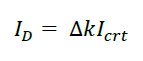 |
(10) |
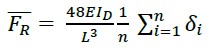 |
(11) |
Com (12), a rigidez atual presente KR é obtida; FR¯ corresponde à força de impacto efetiva média e FR¯ à média dos deslocamentos medidos no campo para cada massa.
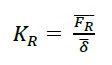 |
(12) |
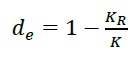 |
(13) |
Em (13), de é considerado um índice de dano e é uma medida da degradação ou diminuição da rigidez, em estruturas saudáveis o valor é nulo, para o colapso é próximo da unidade e depende das características de cada estrutura. No método proposto, a pré-carga do sistema corresponde à carga permanente da estrutura, que pode ser da ordem de até 85% da capacidade total da mesma, o que permite utilizar pequenos incrementos de carga para obter deformações em zonas avançadas do envelope da curva de tensão x deformação de histerese.
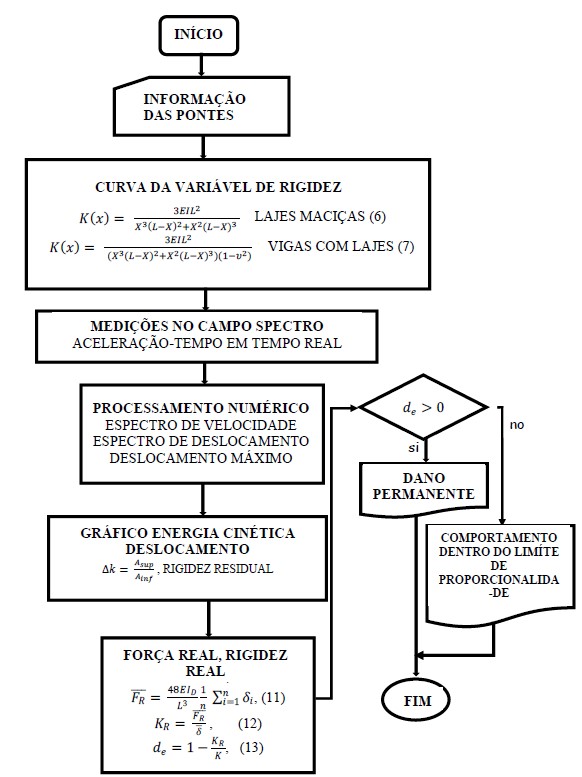
A Figura 3 mostra o fluxograma da metodologia utilizada para os estudos de caso; Em primeiro lugar, é necessário ter as plantas estruturais do projeto. Para medições em campo, é utilizado um sistema de massa que durante o impacto são acoplados ao movimento da estrutura para evitar rebote, preferencialmente, a quantidade de massa para cada grupo de ensaios deve ter valores proporcionais, a fim de facilitar os cálculos correspondentes . É muito importante que ao escolher as massas de ensaio, a aceleração de resposta da estrutura seja pelo menos 20% abaixo do limite máximo de aceleração do sensor e que os valores de aceleração para cada massa diferente tenham discriminação suficiente para processamento numérico. As demais atividades são apresentadas na mesma figura.
 |
||||
| Figura 3. Diagrama de fluxo, Método da variável de rigidez. | ||||
3. Casos de estudo
As pontes instrumentadas estão localizadas na rodovia federal 14, Hermosillo-Moctezuma, no estado de Sonora, Mex.; uma das pontes leva o nome de "El Testarazo" figura 4, que está localizada no km 23 + 900. A ponte possui uma superestrutura composta por três lajes de concreto armado, simplesmente apoiadas em contrafortes constituídos por paredes de concreto armado. A outra ponte instrumentada é chamada de "El Gavilán" figura 5; A superestrutura é formada por um sistema de vigas, lajes e diafragmas de concreto armado, com seção enviesada em 48° em sua direção transversal, localizada no Km 60 + 100 da mesma via.
3.1. Informação dos casos de estudo.
 |
||||
| Figura 4. Geometria superestrutura ponte “Testarazo” (Acot. m). | ||||
 |
||||
| Figura 5. Geometria superestrutura ponte “El Gavilán” (Acot. m). | ||||
As propriedades geométricas das seções transversais foram obtidas sob o critério da seção transformada, e os dados do projeto foram obtidos do Projeto Tipo de Elementos de Concreto Armado, Parte I, publicado pela extinta SAHOP.
| Tabela 1. Propriedades geométricas seção transformada das pontes (m). | ||||||||||||||
| Ponte | bw | hf | bf | n | As(m2) | d | kd | Icrt(m4) | A(m2) | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Testarazo | 5.2 | 0.30 | 10.0 | 8.796 | 0.035 | 0.645 | 0.1858 | 0.1108 | 2.95 | |||||
| El Gavilán | 1.08 | 0.18 | 7.5 | 8.796 | 0.0386 | 2.182 | 0.481 | 1.199 | 2.89 | |||||
Para a ponte “El Testarazo” EI = 2.595 MN- m² (para a rigidez da cerâmica maciça); para a ponte El Gavilan EI = 28.082 MN-m² (para a rigidez da viga). Com esses valores foi obtida a curva de rigidez. Em ambos os casos, apenas os efeitos de flexão são considerados. O valor do módulo de elasticidade do concreto foi considerado E = 23,414 MPa, com base na expressão E = 15100 √(ƒc')(Kg/cm2).
3.2. Curva da variável de rigidez.
As figuras 6 e 7 mostram os gráficos dos cofatores correspondentes aos invariantes de rigidez para as pontes El Testarazo e El Gavilán, respectivamente, obtidos de (4) para a ponte El Gavilán e de (5) para El Testarazo. Os valores de rigidez do projeto KE no centro do vão da superestrutura das pontes em estudo são apresentados na tabela 2; os referidos valores resultam do produto dos cofatores ilustrados nas Figuras 6 e 7 com os respectivos valores EI para cada ponte.
| Tabela 2. Valores de rigidez sob o limite de proporcionalidade. | ||||||||||||||
| Ponte | “El Testarazo” | “El Gavilán” | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| KE(MN/m) | 66.432 | 41.237 | ||||||||||||
 |
||||
| Figura 6. Cofator de rigidez ponte “El Testarazo” | ||||
 |
||||
| Figura 7. Cofator de rigidez ponte “El Gavilán” | ||||
3.3. Procedimento para obter a rigidez real da estrutura.
As medições de campo foram feitas usando uma estrutura para levantamento e descarregamento das massas de excitação, o equipamento consiste em um esqueleto quadrúpede que permite o levantamento das massas por meio de um guincho de capacidade 2250 N; o mecanismo de retenção do recipiente é constituído por um eletroímã com capacidade de 6 KN que permite que a massa de excitação seja fixada por meio de um gancho de segurança com um grau de liberdade de torção (fig. 8).
 |
||||
| Figura 8. Aparência geral do equipamento de ensaio de campo. | ||||
Foram utilizados recipientes de areia, com comportamento plástico durante o impacto, para evitar rebote. Foram fabricados três sacos de 25, 50 e 75kg de capacidade, os quais foram preenchidos até a massa de ensaio; o impacto foi conseguido elevando-se os sacos a uma altura média de 1,50m, posteriormente, o fluxo elétrico do eletroímã que os segurava foi interrompido para liberá-los e produzir o impacto na superfície de apoio da ponte.
O restante do equipamento é composto por um sensor de aceleração de baixa frequência (0,2 Hz), com sensibilidade de 500 mV / g, colocado no centro do vão que permitiu obter a resposta da ponte em tempo real, além de uma cartão de captura de 4 canais para recepção de 0 a 25 khz; a placa permitiu a captura de sinais analógicos produzidos pelo sensor durante as medições. A placa de captura foi colocada em um chassi com capacidade para oito placas de 11-30 V de 15 W, para operar de -40º a 70º C comunicadas à porta USB do computador portador do software para processar o sinal analógico onde foram obtidos os espectros de aceleração - tempo de resposta da estrutura;
Os sinais analógicos capturados foram processados no Software Labview Signal Express versão 3.0, licença 501701A-00, que permitiu a captura do espectro aceleração-tempo em uma matriz numérica em formato TXT de código ASCII, em estado bruto para processamento numérico. Os espectros de aceleração-tempo obtidos são apresentados nas Figuras 9, 10 e os deslocamentos foram obtidos integrando os espectros com o método de aceleração média constante e aceleração linear.
3.4. Resultado das medições em campo.
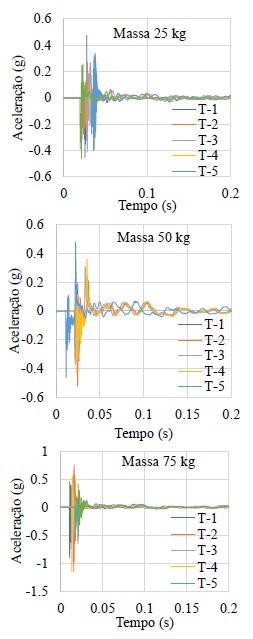
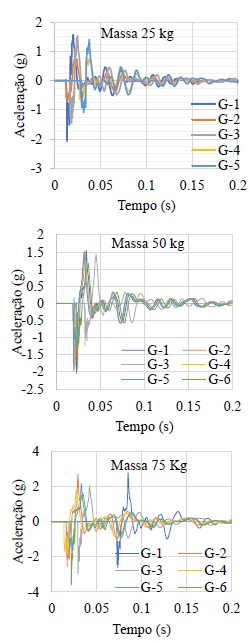
As Figuras 9 e 10 apresentam os espectros de tempo de aceleração capturados durante as medições de campo.
 |
||||
| Figura 9. Espectro aceleração-tempo real, ponte “El Testarazo” | ||||
 |
||||
| Figura 10. Espectro aceleração-tempo real, ponte “El Gavilán” | ||||
Os espectros de aceleração das Figuras 9 e 10 foram submetidos a um tratamento numérico, que consistiu, primeiro, na correção da linha de base espectral e, posteriormente, na dupla integração com os métodos já descritos para obter os deslocamentos máximos produzidos pelo impacto das massas. As tabelas 3 e 4 mostram os resultados que incluem a massa de ensaio, a altura de queda livre e os deslocamentos obtidos no processamento numérico.
| Tabela 3. Resultado de campo e processo numérico puente El Testarazo. | ||||||||||||||
| Massa (Kg) | Altura (m) | Deslocamentos (m) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 25 | 1.525 | -2.92927E-05 | ||||||||||||
| 25 | 1.5 | -2.89101E-05 | ||||||||||||
| 25 | 1.484 | -2.84981E-05 | ||||||||||||
| 25 | 1.46 | -2.8037E-05 | ||||||||||||
| 25 | 1.48 | -2.83313E-05 | ||||||||||||
| 25 | 1.55 | -2.98126E-05 | ||||||||||||
| 50 | 1.38 | -5.11297E-05 | ||||||||||||
| 50 | 1.53 | -5.69176E-05 | ||||||||||||
| 50 | 1.55 | -5.76141E-05 | ||||||||||||
| 50 | 1.47 | -5.473E-05 | ||||||||||||
| 50 | 1.548 | -5.7467E-05 | ||||||||||||
| 50 | 1.56 | -5.77907E-05 | ||||||||||||
| 75 | 1.51 | -8.83783E-05 | ||||||||||||
| 75 | 1.49 | -8.69951E-05 | ||||||||||||
| 75 | 1.5 | -8.74758E-05 | ||||||||||||
| 75 | 1.51 | -8.85254E-05 | ||||||||||||
| 75 | 1.49 | -8.7103E-05 | ||||||||||||
| Tabela 4. Resultados de campo e processo numérico puente El Gavilán | ||||||||||||||
| Massa (Kg) | Altura (m) | Deslocamentos (m) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 25 | 1.54 | -0.000167776 | ||||||||||||
| 25 | 1.52 | -0.000141068 | ||||||||||||
| 25 | 1.55 | -0.00017 | ||||||||||||
| 25 | 1.5 | -0.00013734 | ||||||||||||
| 25 | 1.53 | -0.000163631 | ||||||||||||
| 50 | 1.5 | -0.000260161 | ||||||||||||
| 50 | 1.53 | -0.000268009 | ||||||||||||
| 50 | 1.52 | -0.000266636 | ||||||||||||
| 50 | 1.5 | -0.00026644 | ||||||||||||
| 50 | 1.54 | -0.000273797 | ||||||||||||
| 50 | 1.5 | -0.000258101 | ||||||||||||
| 75 | 1.67 | -0.000491775 | ||||||||||||
| 75 | 1.5 | -0.000440763 | ||||||||||||
| 75 | 1.52 | -0.000448023 | ||||||||||||
| 75 | 1.4 | -0.000412609 | ||||||||||||
| 75 | 1.39 | -0.000408783 | ||||||||||||
| 75 | 1.41 | -0.000414767 | ||||||||||||
3.5. Análise estatística de dados obtidos em campo.
Para saber a validade dos dados obtidos nas medições feitas em uma escala natural dos casos de estudo, procedeu-se à análise de variância ou ANOVA; O objetivo principal é saber com a análise bifatorial se os deslocamentos obtidos são dependentes da massa e altura em queda livre utilizadas nos ensaios e descartar a possibilidade de outros fatores terem influenciado os resultados. A hipótese nula H0 assume que os resultados obtidos são independentes dos fatores de ensaio; a hipótese alternativa H1 assume que os resultados são dependentes de pelo menos um dos fatores, ambos, para um valor de confiança de 95%.
3.5.1. Análise de variância para os dados da tabela 3.
| Tabela 5. Análise de variância bifatorial “El Testarazo”. | ||||||||||||||
| Graus de liberdade | Soma de quadrados | Média de quadrados | F | Valor crítico de F | f | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Regressão | 2 | 1.04213E-08 | 5.2107E-09 | 2866.0866 | 4.2148E-20 | 0.05146909 | ||||||||
| Restos | 15 | 2.72706E-11 | 1.818E-12 | |||||||||||
| Total | 17 | 1.04486E-08 | ||||||||||||
Como a função de distribuição f < F, a hipótese nula H0 é descartada e a hipótese alternativa é aceita; portanto, afirma-se que os resultados de deslocamento obtidos são dependentes de pelo menos um dos fatores massa e / ou altura de queda livre com um valor de confiança de 95%.
| Tabela 6. Análise de variâncias (massa-deslocamento) “El Testarazo”. | ||||||||||||||
| Origem das variações | Soma de cuadrados | Graus de liberdade | Média de quadrados | F | Probabilidade | Valor crítico para F | f | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Entre grupos | 20018.428 | 1 | 20018.4283 | 93.677634 | 5.0095E-11 | 4.1490974 | 0.0039 | |||||||
| Dentro dos grupos | 6838.2352 | 32 | 213.694853 | |||||||||||
| Total | 26856.663 | 33 | ||||||||||||
Como no caso bifatorial, a partir dos valores da Tabela 6, a hipótese nula é descartada e a hipótese alternativa é aceita, pois f <F; pode-se afirmar que os deslocamentos obtidos são dependentes da massa aplicada com um valor de confiança de 95%.
| Tabela 7. Análise de variâncias (altura-deslocamento) “El Testarazo”. | ||||||||||||||
| Origem das variações | Soma de cuadrados | Graus de liberdade | Média de quadrados | F | Probabilidade | Valor crítico para F | f | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Entre grupos | 19.17911772 | 1 | 19.1791 | 20252.1 | 2.061E-46 | 4.149097 | 0.00399 | |||||||
| Dentro dos grupos | 0.03030448 | 32 | 0.00095 | |||||||||||
| Total | 19.2094222 | 33 | ||||||||||||
Como pode ser visto na tabela 7, f <F o que permite descartar a hipótese nula, portanto os deslocamentos obtidos são dependentes das alturas de queda das massas com um valor de confiança de 95%.
3.5.2. Análise de variância para os dados da tabela 4.
| Tabela 8. Análise de variância bifatorial “El Gavilán”. | ||||||||||||||
| Graus de liberdade | Soma de quadrados | Média dos quadrados | F | Valor crítico de F | f | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Regressão | 2 | 2.22636E-07 | 1.1E-07 | 322.93 | 1.93519E-12 | 0.051481683 | ||||||||
| Restos | 14 | 4.82596E-09 | 3.4E-10 | |||||||||||
| Total | 16 | 2.27462E-07 | ||||||||||||
A Tabela 8 apresenta os resultados da análise de variância; uma vez que f <F, a hipótese nula H0 é descartada e a hipótese alternativa é aceita; Portanto, afirma-se que os resultados de deslocamento obtidos são dependentes de pelo menos um dos fatores massa e / ou altura de queda livre com um valor de confiança de 95%.
| Tabela 9. Análise de variâncias (massa-deslocamento) “El Gavilán”. | ||||||||||||||
| Origem das variações | Soma de cuadrados | Graus de liberdade | Média de quadrados | F | Probabilidade | Valor crítico para F | f | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Entre grupos | 22518.64 | 1 | 22518.6391 | 105.37 | 1E-11 | 4.14909744 | 0.00399430 | |||||||
| Dentro dos grupos | 6838.235 | 32 | 213.694852 | |||||||||||
| Total | 29356.87 | 33 | ||||||||||||
Da análise da Tabela 9, a hipótese nula é descartada e a hipótese alternativa é aceita uma vez que f <F; pode-se afirmar que os deslocamentos obtidos são dependentes da massa aplicada com um valor de confiança de 95%.
| Tabela 10. Análise de variâncias (altura-deslocamento) “El Gavilán”. | ||||||||||||||
| Origem das variações | Soma de cuadrados | Graus de liberdade | Média de quadrados | F | Probabilidade | Valor crítico para F | f | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Entre grupos | 19.31294 | 1 | 19.312944 | 9230.5 | 6E-41 | 4.1490974 | 0.0039943 | |||||||
| Dentro dos grupos | 0.066953 | 32 | 0.0020922 | |||||||||||
| Total | 19.3799 | 33 | ||||||||||||
Conforme ilustrado na Figura 10, f <F; a hipótese nula é descartada, de forma que os deslocamentos obtidos são dependentes das alturas de queda das massas com um valor de confiança de 95%.
A decisão quanto à análise de variância dos dados obtidos nas medições de campo de ambas as pontes; pode-se afirmar que os resultados dos deslocamentos medidos dependem das massas utilizadas no impacto e suas alturas de queda livre com um nível de confiança de 95%, da mesma forma, também se afirma que são os fatores de maior influência com uma probabilidade maior que 99%.
3.6. Estimativa do fator de dano.
A partir do processamento numérico dos sinais das Figuras 8 e 9, foram obtidos os espectros de velocidade e deslocamento; Conhecendo as alturas de queda das massas, procedemos à construção dos gráficos energia cinética-deslocamento, utilizando (9) para estimar a energia cinética. As Figuras 11 e 12 mostram os gráficos de energia cinética em relação aos deslocamentos médios para os dois casos de estudo.
 |
||||
| Figura 11. Relação Energia Cinética-deslocamento, ponte “El Testarazo” | ||||
 |
||||
| Figura 12. Relação Energía Cinética-deslocamento, ponte “El Gavilán” | ||||
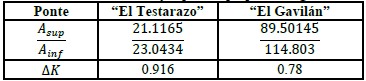
Os valores obtidos para a redução por dano do momento de inércia de acordo com (10) e (11), são apresentados na tabela 11; as áreas correspondem às superfícies superior e inferior dos 3 pontos.
| Tabela 11. Valores de modificação para as propiedades geométricas (I). | ||||||||||||||
 | ||||||||||||||
4. Resultados
Para obter as forças efetivas que definiram os valores da rigidez real presente em função do impacto das massas dos ensaios de campo, (11) foi aplicado.
A Tabela 12 mostra os resultados das forças e dos deslocamentos médios obtidos que serviram para obter os valores médios da rigidez real do ponto das superestruturas dos casos em estudo.
| Tabela 12. Valores de forças efetivas e deslocamentos médios. | ||||||||||||||
 | ||||||||||||||
Com os valores médios dos deslocamentos e das forças reais obtidas, aplicando-se (12) os valores da rigidez real dos elementos em estudo foram obtidos. O contraste foi realizado com os valores obtidos do produto EI pelos cofatores invariantes de rigidez ilustrados nas Figuras 6 e 7, respectivamente, para cada ponte; os resultados são apresentados na tabela 13.
| Tabela 13. Valores de rigidez real, rigidez de projeto e porcentagem de dano. | ||||||||||||||
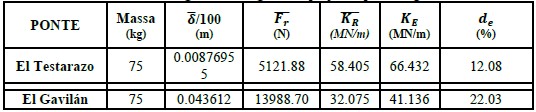 | ||||||||||||||
Avaliando o status dos estudos de caso, é importante esclarecer que o índice de danos para estruturas saudáveis deve ter um valor nulo; de acordo com a Tabela 14, que resume os resultados obtidos, afirma-se o seguinte: Para a ponte "El Testarazo" construída com lajes maciças, o valor do índice de avaria é de 12,08%, o que indica que a estrutura tem 87,9% do seu original capacidade; Pode-se interpretar que, ao longo da vida útil, a superestrutura perdeu rigidez de 12,08% em relação ao estado original, acumulando danos irreversíveis, que se manifestam (manifestação patológica) por deflexão excessiva e fissuras transversais alternadas no centro do vão.
A evidência apresentada na fig. (10), onde se pode observar que os três pontos obtidos para as diferentes massas formam duas retas com diferentes inclinações com comportamento decrescente, mostrando que o estado da estrutura ultrapassou o limite de proporcionalidade. No caso da ponte “El Gavilán” construída com vigas, lajes e diafragmas de concreto armado com desvio de 48 °, o índice de avarias resultante é de 22,03%, o que indica que tem uma capacidade de 77,97% em relação à sua capacidade projetada, que combina rachaduras e curvatura excessiva na estrutura. É importante esclarecer que a rigidez ao deslocamento vertical depende da contribuição para a flexão e torção (Deng Kai, 1998).
Sob esta consideração, o índice de dano calculado expresso na tabela 13 inclui a redução da rigidez à flexão e torção, mas não é possível distinguir qual porcentagem corresponde a cada grau de liberdade.
5. Conclusões
O uso da invariante de rigidez permitiu obter valores de índices de danos dos casos estudados de acordo com suas condições físicas. O procedimento é relativamente simples, principalmente quando se dispõe das informações utilizadas na sua construção. A facilidade na análise para obter os dados de comparação, assim como a facilidade com que os valores reais de rigidez são obtidos na atualidade, são as principais vantagens do método.
As desvantagens que existem, sobretudo, correspondem à etapa de medição em campo, uma vez que requer condições ambientais de temperatura constante e a ausência de vento. Outra desvantagem é que para pontes esconsas, uma análise mais refinada é necessária para obter a variável de rigidez, uma vez que os percentuais de redução correspondentes tanto à rigidez à flexão quanto à rigidez por torção não são apreciados com o procedimento proposto.
O método é regido por princípios energéticos, pode ser utilizado em estruturas de concreto armado e protendido com uma aproximação aceitável, pois a quantidade de energia de deformação inclui a área da região que forma as secantes com a curva força-deslocamento real e corresponde ao erro do método. Este erro é uma pequena porção do trabalho realizado que é adicionada à energia de deformação, portanto as massas de ensaio devem ser escolhidas com os menores incrementos possíveis a fim de minimizar o erro ou, na falta disso, estimar o erro logisticamente ajustando os três pontos e obtenção da área dos arcos a ser subtraída da energia de deformação e adicionada ao trabalho realizado. O desenvolvimento de ajuste por engano está fora do escopo deste trabalho.
Outra limitação na utilização do método é que o peso da própria estrutura seja parte importante da carga de serviço, por isso é recomendado para uso em pontes de laje e vigas.
REFERÊNCIAS
LCPC Balmes, E., Corus, M., Siegert, D. (1998). Modeling thermal effects on bridge dynamic responses, Ecole Centrale Paris/MSSMat, SDTools, balmes@sdtools.com.
Publicación Técnica No. 132 Carrión Viramontes, F. J., Lozano Guzmán, A., Fabela Gallegos, M., Vázquez Vega, D., Romero Navarrete, J. A. (1999). “Evaluación de puentes mediante el análisis de vibraciones ”, Instituto Mexicano del Transporte, , ISSN: 0188-7297. URL: http://www.imt.mx/archivos/Publicaciones/PublicacionTecnica/pt132.pdf
Publicación Técnica No. 379 Crespo Sánchez, S. E., Carrión Viramontes, F., Quintana Rodríguez, J. A., Hernández Guzmán, A., López López, J. A. (2013), “Análisis del deterioro estructural por fatiga y prognosis de un puente típico de concreto utilizando simulación MonteCarlo”, Instituto Mexicano del Transporte, , ISSN: 0188-7297, URL: https://imt.mx/archivos/Publicaciones/PublicacionTecnica/pt379.pdf
Deng, K. (1998), “Dynamic response of certain types of highway bridges to moving vehicles”, Phd. Thesis, The Doctor of Philosophy program in Civil and Environmental Engineering is a joint program with the University of Ottawa administered by The Ottawa-Carleton Lnstitute for Civil Engineering. URL: https://www.collectionscanada.gc.ca/obj/s4/f2/dsk2/ftp02/NQ37062.pdf
Singer, F. L. (1975), “Engineering Mechanics: Statics and Dynamics ”, Third Edition, Harper & Row, New York, I.S.B.N. 968-6034 16-1.
Imhof, D. (2004). Risk assessment of existing bridge structures. (Doctoral thesis) University of Cambridge. https://doi.org/10.17863/CAM.19092
Valdés, J., De la Colina, J. (2008). Análisis de la Amplificación Dinámica de la Carga Viva en Puentes con Base en Pruebas Experimentales. Revista Tecnológica - ESPOL, 21(1), 149 - 156. Recuperado a partir de http://www.rte.espol.edu.ec/index.php/tecnologica/article/view/150
Luthe, R. (1971), “Análisis Estructural”, Representaciones y Servicios de Servicios de Ingeniería, S. A. México.
MIS27 Maldonado, E., Canas, J., Casas, J., Pujades, L. (1998), Respuesta de puentes frente a acciones sísmicas, Monograph Series in Earthquake Engineering, editor A. H. Barbat. , ISBN: 84-89925-23-2, URL: https://www.scipedia.com/public/Maldonado_et_al_2019a
392 Munirudrappa, N., Dhrujavara Iyengar, H. N. (1999), “Dynamic Analysis of Continuous Span Highway bridge”, ISET Journal of Earthquake Technology, No. , 36 (1), 73 - 84. URL: http://home.iitk.ac.in/~vinaykg/Iset392.pdf
Park, R., Paulay, T. (1988), “Estructuras de Concreto Reforzado”, Editorial Limusa, S. A. de C. V. México, D. F., Cuarta reimpresión, I.S.B.N. 968-18-0100-8.
Perdomo, M. E., Castro, L., Picón, R., Marante, M. E., Flórez-López, J. (2006). Modelo de daño para elementos de concreto armado sometidos a corte y flexión. Revista de la Facultad de Ingeniería Universidad Central de Venezuela, 21(4), 23-36. ISSN 0798-4065.
Cuarta colección Secretaría de Asentamientos Humanos y Obras Públicas (1980), “Puentes para Carreteras. Proyectos Tipo de Elementos de Concreto Reforzado. Parte I.”, . Diciembre de 1980, México, Editado por SAHOP.
Timoshenko, S., Woinowsky-Krieger, S. (1989), “Theory of plates and Shells”, Second edition, McGRAW-HILL BOOK COMPANY, New York, ISBN 0-07-064779-8.
Vélez Gómez, W. H., Riveros Jerez, C. A. (2011), “Caracterización dinámica en condiciones de excitación natural de puentes de concreto reforzado”, Vector, 6, 36 - 44.
