Investigación Aplicada

https://doi.org/10.21041/ra.v10i1.448

Análisis numérico de la sección de losas de hormigón compuesto y acero bajo incendio

Numerical analysis of composite concrete and steel slabs section under fire situation

Análise numérica das características da seção de lajes mistas de aço e concreto em situação de incêndio

F. Barcellos¹ , F. Bolina² , B. Tutikian^{2 *}

¹ Master student in Graduate Program of Architecture and Urbanism, Universidade do Vale do Rio dos Sinos, São Leopoldo, Brazil. .

^² itt Performance, Universidade do Vale do Rio dos Sinos, São Leopoldo, Brazil. .

^* Autor de Contato: btutikian@terra.com.br

Recepción: 29 de julio de 2019.
Aceptación: 11 de diciembre de 2019.
Publicación: 30 de diciembre de 2019

Citar como: Barcellos, F., Bolina, F., Tutikian, B. (2020), "Numerical analysis of composite concrete and steel slabs section under fire situation", Revista ALCONPAT, 10 (1), pp. 69 – 78, DOI::https://doi.org/10.21041/ra.v10i1.448

RESUMEN
Este trabajo tiene como objetivo evaluar el rendimiento de las losas compuestas bajo fuego, correlacionándolas con el proyecto a temperatura normal, de acuerdo con NBR 14323 (ABNT, 2013), NBR 8800 (ABNT, 2008) y NBR 14762 (ABNT, 2010), a través de la curva de calentamiento de ISO 834 (ISO, 1999) y la distribución de las temperaturas de losas obtenidas utilizando el software Ansys. Los modelos computacionales fueron calibrados de acuerdo con el estándar y extrapolados a otros escenarios de diseño, con diferentes geometrías, espesores y espesores efectivos de la capa de concreto. Como resultado, la plataforma con rebajes tuvo un mejor rendimiento en relación con los trapecios, siendo el espesor de la capa de hormigón la variable preponderante en el comportamiento de estas losas a altas temperaturas, debido a su mayor estabilidad térmica.
Palabras clave: seguridad contra incendios, losas compuestas, acero, hormigón

ABSTRACT
This work aims to evaluate the performance of composite slabs under fire, correlating them to the project at normal temperature, according to NBR 14323 (ABNT, 2013), NBR 8800 (ABNT, 2008) and NBR 14762 (ABNT, 2010). ), through the heating curve of ISO 834 (ISO, 1999) and distribution of slab temperatures obtained by using Ansys software. The computational models were calibrated according to the standard and extrapolated to other design scenarios, with different geometries, thicknesses and effective thicknesses of the concrete layer. As results, the steel deck with recesses had better performance in relation to the trapezoids, being the thickness of the concrete layer the preponderant variable in the behavior of these slabs at high temperatures, due to their greater thermal stability.
Keywords: fire safety, composite slabs, steel, concrete

RESUMO
Este trabalho busca avaliar o desempenho de lajes mistas de aço e concreto em situação de incêndio, correlacionando-as ao projeto em temperatura ambiente, conforme NBR 14323 (ABNT, 2013), NBR 8800 (ABNT, 2008) e NBR 14762 (ABNT, 2010), através da curva de aquecimento da ISO 834 (ISO, 1999) e distribuição de temperaturas obtidas segundo o software Ansys. Os modelos computacionais foram calibrados pela norma e extrapolados computacionalmente. Foram analisadas lajes com chapas trapezoidais de diferentes geometrias e com camadas de concreto variadas. Como resultados, as chapas com reentrâncias apresentaram melhor desempenho face às trapezoidais, sendo a espessura da camada de concreto preponderante no comportamento destas lajes ao incêndio, visto a sua maior estabilidade térmica.
Palavras-chave: segurança contra incêndio, lajes mistas, aço, concreto

1. IntroducciÓn

Las losas compuestas poseen algunas ventajas constructivas en comparación a sistemas tradicionales. Ellas ofrecen una plataforma de trabajo durante la ejecución de la estructura, velocidad de construcción, aumento de la estabilidad local y global de la estructura de acero, reducción de la altura de las vigas y del propio peso de la estructura (Craveiro, 2010; Liang, 2015). A pesar de ser una solución empleada, la sensibilidad al fuego del acero exige mayor atención en proyecto (Li; Wang, 2013). La sensibilidad de los materiales metálicos a las altas temperaturas fundamenta esta discusión. En el caso de estas losas, la esbeltez de la chapa perfilada incorporada puede proporcionar rápida quiebra y ruptura brusca, como mencionado por Li et.al.,2017.

El análisis de las estructuras mistas en altas temperaturas elaborado en Builing Research Establisment en la década de 90, en Cardington, en Inglaterra, motivados por incendios en edificios altos, como el del One Meridian Plaza, en los Estados Unidos (1991), y BroadGate, en Inglaterra (1990), mostraron un desempeño superior al esperado de las losas compuestas, que no presentaron colapso (Selamet; Bolukbas, 2016). Su interacción con la viga de redistribución de esfuerzos promovió la movilización del efecto de la membrana (Nguyen et.al.,2015), que mejoró su resistencia al fuego. Discusiones sobre el conservadorismo de las normas surgieron (Bailey et.al., 2000), fase al fenómeno notado - de difícil previsión al nivel del proyecto (Gillie et.al., 2001) - que demostró que estructuras metálicas poseían una resistencia al fuego inherente, no identificadas en simulaciones y/o verificaciones numéricas (Omer et.al., 2009)

En los estudios realizados en Cardington, en Reino Unido, fue constatado que la geometría de la losa compuesta tiene un papel importante en la distribución de la temperatura en la plataforma, influenciando su resistencia al fuego (Li et al2017). El relieve de la losa hace que la humedad del concreto en este local demore más para evaporar, disminuyendo generalizadamente la temperatura del concreto. La espesura de la chapa de acero no influencia en la distribución de la temperatura en la losa, ya que su pequeña dimensión hace con que su promedio de temperatura sea prácticamente igual en todos los casos, con promedios de valores semejantes (Li, Wang, 2013).

El concreto también tiene gran influencia sobre el comportamiento de las losas compuestas expuestas en incendios. Debido a su baja conductividad térmica, cuanto mayor la espesura de su recubrimiento, menor es la consecuencia de las altas temperaturas en la losa, que presenta una mayor resistencia al fuego (Li, Wang, 2013), en este caso, el efecto de la membrana se desarrolla mejor en estos casos. El desprendimiento del concreto tiende a ser más leve en estas losas, como ya comprobamos en la barrera proporcionada por la chapa perfilada (Costa et al, 2002; Wang, 2002).

La verificación de las estructuras mistas de acero y el concreto en situación de incendio es hecho por NBR 14323 (ABNT, 2013), con fuerte inspiración en EN 1994-1-2 (EN, 2005). Ella especifica que el proyecto de estas estructuras en alta temperatura debe ser hecho en el último estado límite (ELU), no siendo necesaria la verificación en el estado límite del servicio (ELS). La norma propone que el dimensionamiento puede ser realizado a través del resultado de ensayos o por métodos analíticos de cálculo.

La verificación estructural de las losas en altas temperaturas pasa por tres criterios: la estanquidad, el aislamiento térmico y la capacidad resistente, siendo que NBR 14323 (ABNT, 2013) considera el criterio de estanquidad atendido con la presencia de la chapa de acero. E criterio del aislamiento térmico es determinado por la espesura efectiva de la losa. Su capacidad resistente es determinada a través del análisis plástico global, considerando los momentos positivos y negativos generados por el cargamento específico y obtenidos a través del diagrama de momentos flectores.

De acuerdo con la norma, la contribución proporcionada por la chapa de acero en el momento resistente es calculada por la adición de la contribución de cada elemento que compone la chapa, de acuerdo Ecuación 1, siendo A_efi el área efectiva de la parte i em cm², d_i la distancia del centro de la gravedad de la parte i hasta la línea neutra de la sección de la losa en cm,f_yk la resistencia al desagüe del acero utilizado en kN/cm² and k_{y,θ i} el coeficiente de reducción de la resistencia del acero de acuerdo a la temperatura indicada para aquel elemento, que es calculada a través de coeficientes indicados en la norma para el tiempo requerido de resistencia al fuego (TRRF) de 60,90 y 120 minutos. . Para el cálculo de la posición del eje neutro en relación a la cara superior de la losa utilizada la Ecuación 2, donde f _{c k} es la resistencia a la compresión del concreto en kN/cm², k_c,θ es el coeficiente de reducción de la resistencia del concreto de acuerdo con la temperatura y b_w es el ancho de la losa.

(1)

(2)

La contribución proporcionada por el concreto es calculada de acuerdo a la Ecuación 3, siendo que A_{e f,c} es el área de contribución del concreto arriba de la línea neutra en cm², d es la distancia del centro de gravedad del área comprimida del concreto hasta la línea neutra en cm, f_ck es la resistencia a la compresión del concreto en kN/cm² y k_c,θ es el coeficiente de reducción de la resistencia del concreto de acuerdo a la temperatura, siendo indicado en norma para TRRF de 60, 90 y 120 minutos.

(3)

El momento resistente final de la losa es calculado como la suma de los momentos resistentes de la chapa de acero y del concreto. El cálculo del cortante no es considerado por esta norma, motivo por el cual no será realizada su evaluación en este trabajo.

A pesar de los estudios que constatan la importancia de la geometría y espesura de la chapa de acero (Li et.al., 2017; Li, Wang,2013), y de existir comercialmente variadas geometrías y espesuras disponibles, las mismas no son llevadas en consideración en el aislamiento térmico, sino en relación al espesor efectivo mínimo de la losa de concreto, de acuerdo a NBR 14323 (ABNT, 2013), mereciendo, por lo tanto, una mayor investigación.

En otras palabras, este trabajo tiene el objetivo de analizar el comportamiento de las losas compuestas, de acero y concreto, en situación de incendio, abordando la influencia de la geometría, del espesor de la chapa de acero y del espesor de la losa de concreto con el tiempo de resistencia al fuego de la losa a través del análisis numérico, calculando la temperatura de la misma de forma computacional de acuerdo con Ansys, basándose en los criterios de dimensionamiento y de verificación de las normas brasileñas y europeas.

2. MÉtodo

La verificación numérica fue basada en ecuaciones de NBR 8800 (ABNT, 2008), NBR 14323 (ABNT, 2013), NBRT 15200 (ABNT, 2012) y Eurocódigos correspondientes, como EN 1992 (CEN, 2010), EN 1994 (CEN, 2004). Como a NBR 14323 (ABNT,2013) presenta orientaciones limitadas de proyecto para diferentes TRRF, fue necesario realizar un análisis computacional para extrapolación de los resultados, a través del software Ansys, utilizando la curva de incendio estándar definida por ISO 834 (ISO, 1999), como requerido por NBR 14323 (ABNT, 2013) para análisis de estas estructuras en altas temperaturas.

Las variables de respuesta propuestas son la espesura de la camada de concreto, la geometría y la espesura de la chapa. La evaluación fue hecha con el objetivo de explorar los valores de una variable mientras las otras dos tienen sus valores fijos. Fueron evaluadas espesuras efectivas de concreto de 80 mm, 90 mm, 100 mm, 110 mm, 120 mm, 130 mm, 140 mm y 150 mm. Entre las geometrías de las chapas estudiadas, fueron escogidas dos trapezoidales y una con hendiduras, como en la Figura 1 y las espesuras de las chapas estudiadas fueron de 0,80 mm, 0,95 mm y 1,25 mm.

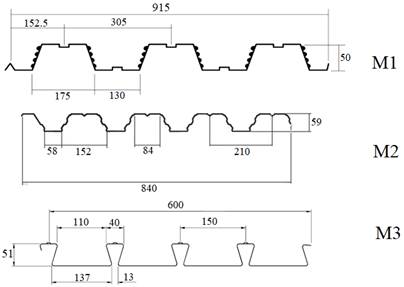Figura 1. Modelos de chapa estudiados

Para denominar los dos modelos estudiados, fue escogido el orden de la nomenclatura, siendo que el primero es la letra M seguido del número de modelo de chapa, después la letra F seguida de la espesura de la chapa y por último la letra C seguida de la espesura efectiva del concreto en milímetros. La figura 2 muestra un ejemplo del montaje de la nomenclatura utilizada en este trabajo.

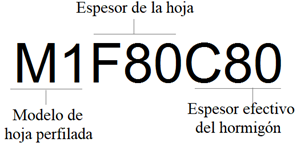
Figura 2. Nomenclatura dos modelos estudiados

Como variables de control, para análisis de las losas permitidas en este estudio, fueron adoptados los valores del acero y del concreto en altas temperaturas, como presentados en la Tabla 1. El modelo de losa estudiada es unidireccional y bi-apoyado, formando elementos isostáticos, de anchura 1 m y van de 3 m. Los apoyos fueron considerados perpendiculares a las tramas. No hay formación de fuerzas de compresión del efecto membrana debido al vínculo del modelo, que, por ser apoyado, no restringe el movimiento horizontal. También no fue considerado el análisis constructivo para las losas compuestas, pues la chapa debe soportar la totalidad de las cargas durante el proceso de cura del concreto. No fue considerada la utilización de armaduras de flexión negativa en los modelos adoptados, y la armadura positiva fue constituida por la chapa perfilada de acero, siendo que el colapso del modelo estudiado se da por rótula plástica sobre momento positivo en sección central.

Tabla 1. Propiedades del acero y del concreto en altas temperaturas
	Propiedades del acero	Propiedades del concreto
Resistencia Característica	Fluencia - Como Tabla 1 da NBR 14323 (ABNT, 2013)	Como Tabla 1 da NBR 15200 (ABNT, 2012)
Coeficiente de Poisson	0,3	0,15
Módulo de Elasticidad	Como Tabla 1 da NBR 14323 (ABNT, 2013)	Como EN 1994-1-2 (EN, 2005)
Conductividad térmica	Como item E.4 do Anexo E de NBR 14323 (ABNT, 2013)	Como tópico C.3 do Anexo C de NBR 15200 (ABNT, 2012)
Calor específico	Como tópico E.43 do Anexo E da NBR 14323 (ABNT, 2013)	Como tópico C.2 do Anexo C da NBR 15200 (ABNT, 2012)
Masa específica	7850 kg/m³	2500 kg/m³

Los TRRF estudiados fueron de 15, 30, 45, 60, 90, 120, 150 y 180 minutos. Como la NBR 14323 (ABNT, 2013) los coeficientes para el cálculo de la temperatura de la chapa de acero solamente para los TRRF de 60 min, 90 min y 12º min, fue utilizado el software Ansys para el alcance de la temperatura de los elementos TRRF no alcanzados por la norma, calibrando las extrapolaciones con los valores presentados por la norma.

Ansys utiliza el método de los elementos finitos en su análisis, con la formación de mallas y análisis de sus puntos de intersección. La herramienta fue empleada para analizar la distribución de la temperatura en la sección, expuesta a la curva estandarizada de incendio de ISO 834 (ISO,1999). El coeficiente de convención utilizado fue de 25 W/m².K. No fue considerada la emisividad térmica de los materiales. La colecta de la temperatura fue hecha a través de la herramienta Temperature Probe do Ansys. Para medir la temperatura de la chapa perfilada, fueron seleccionadas faces expuestas al fuego, adoptando como punto de medida el plano medio del respectivo elemento que compone la chapa. En la medición de las temperaturas del concreto fue admitida la parte comprimida de la sección.

3. Resultados

Las Figuras 3, 4 y 5 muestran la temperatura promedia de la fase superior del concreto superior de la línea neutra.

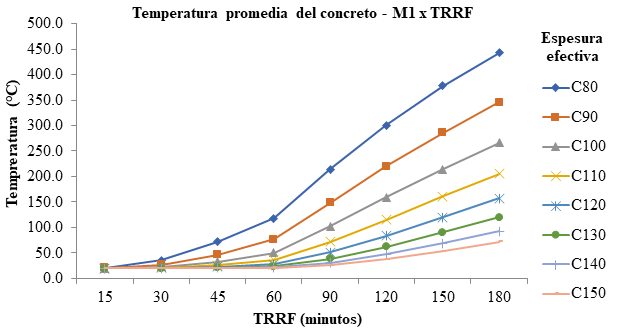Figura 3. Temperatura promedio del concreto con chapa M1

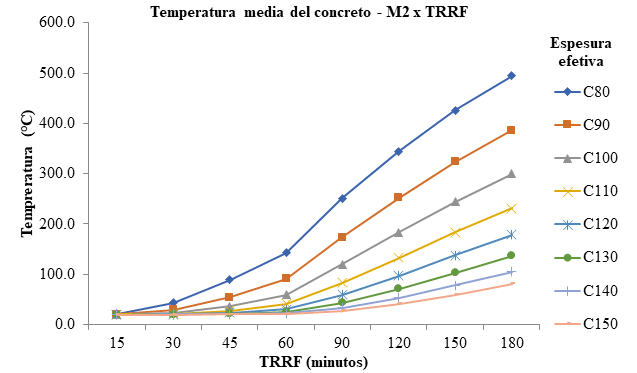
Figura 4. Temperatura promedio del concreto con chapa M2

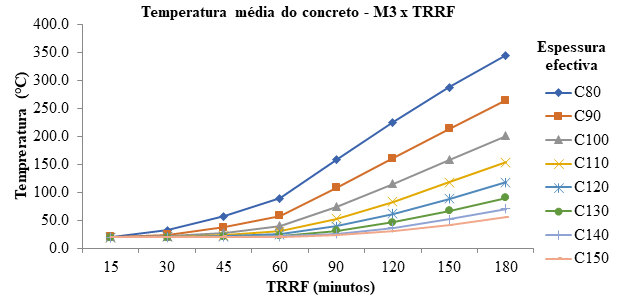
Figura 5. Temperatura promedio del concreto con chapa M3

Se nota que, solo a los 60 min de exposición, la variable de la temperatura es mayor y más significativa en las cuatro primeras espesuras, ultrapasando 100°C y comprometiendo su resistencia. A los 180 min., solamente el modelo M1 con espesuras de 14 y 15 cm, el modelo M2 con espesura de 15cm y el modelo M3 con espesuras de 13 a 15 cm no alcanzaron 100°C. En otras espesuras, las temperaturas llegaron a 494,5°C, teniendo un coeficiente de reducción de 0,61. Este comportamiento de aislamiento térmico del concreto puede ser explicado por su baja conductividad térmica y alto calor específico, lo que hace con que en fase de una exposición al fuego necesite de alta temperatura y duración para que el calor sea transferido a lo largo de su espesura. Analizando la temperatura de la chapa cuando verificada su geometría en la exposición a altas temperaturas, son obtenidas temperaturas muy semejantes para la mesa inferior y alma, lo que era de esperarse, por la elevada conductividad térmica del acero.

Son presentados, en las Tablas 2, 3 y 4, los factores de reducción de resistencia al desagüe de las diferentes partes de la chapa. La geometría de la chapa del modelo M3 tiene la mayor variante de temperatura en los elementos, presentando las menores temperaturas de mesa superior y las mayores temperaturas de mesa inferior y alma entre los modelos estudiados. Como consecuencia, estas chapas poseen mayores factores de reducción en la mesa superior y los menores en la mesa inferior y alma. Esta variante está dentro de una línea de 133°C y es influenciada por el área y forma de exposición de la misma, que, por causa del modelo con hendiduras, acaba aislando la mesa superior y dejando un área mayor de exposición en la mesa inferior, que es transferida para el alma.

Tabla 2. Factor reduccional de resistencia a la escorrentía de la mesa superior
Modelo	15 min	30 min	45 min	60 min	90 min	120 min	150 min	180 min
M1	1,00	0,72	0,42	0,25	0,12	0,08	0,06	0,05
M2	1,00	0,79	0,47	0,30	0,15	0,09	0,08	0,07
M3	1,00	0,89	0,64	0,43	0,22	0,13	0,10	0,09

Tabla 3. Factor de reducción de resistencia a la escorrentía de la mesa inferior
Modelo	15 min	30 min	45 min	60 min	90 min	120 min	150 min	180 min
M1	1,00	0,65	0,34	0,20	0,09	0,06	0,05	0,04
M2	1,00	0,61	0,28	0,16	0,08	0,05	0,05	0,05
M3	1,00	0,52	0,24	0,14	0,07	0,05	0,05	0,04

Tabla 4. Factor de reducción de resistencia a la escorrentía del alma
Modelo	15 min	30 min	45 min	60 min	90 min	120 min	150 min	180 min
M1	1,00	0,65	0,34	0,20	0,09	0,06	0,05	0,04
M2	1,00	0,61	0,28	0,16	0,08	0,05	0,05	0,05
M3	1,00	0,52	0,24	0,14	0,07	0,05	0,05	0,04

La temperatura de la chapa no sufrió variable significativa con el cambio de espesura, atribuido a la elevada conductividad térmica del acero y a las dimensiones reducidas de la espesura de la chapa. En el modelo de cálculo de NBR 14323 (ABNT,2013), solamente la geometría del modelo de chapa influencia en la variación de la temperatura, siendo que ella es igual para todas las espesuras de un mismo modelo. Este procedimiento fue confirmado con la verificación en Ansys, pues la variación no ultrapasó 1% entre espesuras.

Correlacionando las variables que influencian en la resistencia de la losa en altas temperaturas (geometría de la chapa y la espesura de la camada de concreto) y haciendo un promedio en función de estos valores con la espesura de la chapa, se puede afirmar que las diferencias de temperatura en función de la geometría son más significativas en las menores espesuras de concreto, disminuyendo de acuerdo al aumento de la espesura, como muestra la Figura 6. A pesar de esto, siempre se observó la ventaja del modelo M3 en relación a los otros modelos. Con el aumento de TRRF, la diferencia de temperatura relativa a la espesura de la camada de concreto fue disminuyendo.

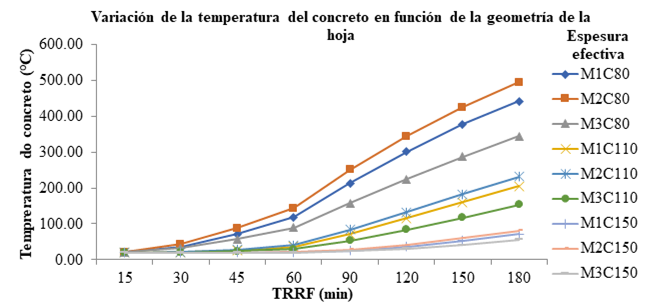Figura 6. Variación de la temperatura del concreto en función de la geometría de la chapa

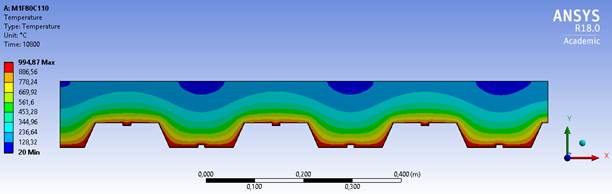
El modelo M1 presenta una geometría semejante al modelo M2 de acuerdo muestran las Figuras 7 y 8, lo que hace con que la variación de la temperatura entre estos dos modelos sea menor. La variable más significativa es entre la geometría del modelo M2 y la del modelo M3, siendo que el primero tiene siempre la mayor temperatura y el segundo la menor temperatura entre los modelos estudiados. Eso se debe al hecho de que la geometría del modelo M2 expone más a su mesa superior, facilitando con que la temperatura alcance valores más altos en el concreto. La geometría del modelo M3 es con hendiduras, lo que permite que el calor se concentre en la mesa inferior de la chapa y dificulte el acceso del aire caliente en la mesa superior, como muestra la Figura 9. Las isotermas muestran también la forma como la temperatura avanza en las losas, siendo que en el modelo M3 ellas se comportan de forma constante, formando líneas rectas, mientras que en los otros dos modelos ellas forman olas.

Figura 7. M1F80C110 con TRRF de 180 minutos

Figura 8. M2F80C110 con TRRF de 180 minutos

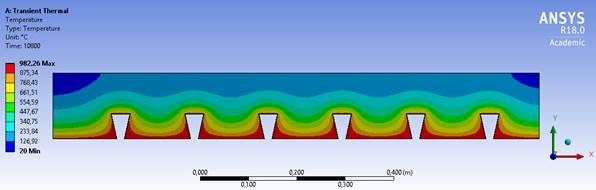
Figura 9. M3F80C110 con TRRF de 180 minutos

La variable que más influenció la temperatura fue la geometría de la hoja de acero, con el modelo M3, con penetrancias, teniendo el mejor desempeño entre los estudiados. Esto se debió a la mayor área de acero unitaria de estos elementos y el mayor consumo de concreto - de mayor estabilidad térmica en las ranuras.

La espesura efectiva de la camada de concreto también se mostró influenciable. Por el concreto tener conductividad térmica baja, cuando mayor su espesura menor fue la temperatura de la parte resistente a la compresión de la losa, local donde el concreto efectivamente actúa en el momento resistente. El inconveniente de esta solución es el aumento de peso de la estructura.

A partir de los 30 minutos de exposición al incendio, el coeficiente de reducción de la hoja de acero muestra que la misma no tiene más participación estructural, dejando el concreto no armado sometido a la flexión. Siendo así, en los análisis numéricos concebidos con base en las ecuaciones normativas, es necesaria la utilización de armadura positiva para evitar la ruptura brusca del concreto en altas temperaturas. Aún, los estudios experimentales nos han mostrado que estas losas poseen una resistencia al fuego intrínseca, ya que fue visto el efecto de la membrana que se forma, difícil de ser previsto numéricamente.

4. Conclusiones

Entre los puntos evaluados en este estudio, los que ejercen mayor influencia sobre el comportamiento de las losas compuestas de concreto y acero son la geometría de la hoja de acero y la espesura de la camada de concreto, respectivamente. Esto ocurre debido principalmente a la estabilidad térmica generada por la geometría que posibilita un mayor consumo de concreto y la baja conductividad térmica del concreto.

Referencias

Associação Brasileira de Normas Técnicas (2013). NBR 14323: Projeto de estruturas de aço e de estruturas mistas de aço e concreto de edifícios em situação de incêndio. Rio de Janeiro.

Associação Brasileira de Normas Técnicas (2008). NBR 8800: Projeto de Estruturas De Aço e de estruturas mistas de aço e concreto de edifícios. Rio de Janeiro.

Associação Brasileira de Normas Técnicas (2010). NBR 14762: Dimensionamento de estruturas de aço constituídas por perfis formados a frio. Rio de Janeiro.

Associação Brasileira de Normas Técnicas (2012). NBR 15200: Projeto de estruturas de concreto em situação de incêndio. Rio de Janeiro.

Bailey, C. G.; White, D. S.; Moore, D. B. (2000). The tensile membrane action of unrestrained composite slabs simulated under fire conditions. Engineering Structures. 22 (12):1583-1595. https://doi.org/10.1016/S0141-0296(99)00110-8

Costa, C. N.; Figueiredo, A. D.; Pignatta, V. (2002). O fenômeno do lascamento (“spalling”) nas estruturas de concreto armado submetidas a incêndio - uma revisão crítica. In: In: 44º Congresso Brasileiro do Concreto- IBRACON 2002. Anais eletrônicos. Belo Horizonte.

Craveiro, H. D. S. (2010). “Análise do comportamento estrutural de lajes mistas aço-betão com reforço transversal”. Dissertação de mestrado. Universidade de Coimbra, Coimbra.

European Committee for Standardization (2005). EN 1994-1-2: Design of composite steel and concrete structures - Part 1-2: General rules - structural fire design: Eurocode 4. Brussels.

Gillie, M.; Usmani, A. S.; Rotter, J. M. (2001). A structural analysis of the first Cardington test. Journal of Constructional Steel Research. 57 (6):581-601. https://doi.org/10.1016/S0143-974X(01)00004-9

Li, G.; Zhang, N.; Jiang, J. (2017). Experimental investigation on thermal and mechanical behaviour of composite floors exposed to standard fire. Fire Safety Journal. 89:63-76. https://doi.org/10.1016/j.firesaf.2017.02.009

Liang, Q. Q. (2015). “Analysis and Design of Steel and Composite Structures”. CRC Press, New York. p. 458. ISBN: 9780415532204

Li, G.; Wang, P. (2013). “Advanced Analysis and Design for Fire Safety of Steel Structures”. China: Zhejiang University Press, Springer-Verlag Berlin Heidelberg. p. 357. ISBN: 9783642343933

Nguyen, T. T.; Tan, K. H.; Burgess, I. W. (2015). Behaviour of composite slab-beam systems at elevated temperatures: Experimental and numerical investigation. Engineering Structures, 82: 199-213. https://doi.org/10.1016/j.engstruct.2014.10.044

Omer, E.; Izzuddin, B. A.; Elghazouli, A. Y. (2009). Failure of lightly reinforced concrete floor slabs with planar edge restraints under fire. Journal of Structural Engineering, 135 (9): 1068-1080. https://doi.org/10.1061/(ASCE)0733-9445(2009)135:9(1068)

Selamet, S.; Bolukbas, C. (2016). Fire resilience of shear connections in a composite floor: Numerical investigation. Fire Safety Journal, 81: 97-108. https://doi.org/10.1016/j.firesaf.2016.02.003

Vargas, M. R.; Silva, V. P. (2005). Resistência ao fogo das estruturas de aço. Rio de Janeiro: IBS/CBCA. Rio de Janeiro. P.78. ISBN: 85-89819-02-7.

Wang, Y. C. (Ed.). (2002). “Steel and Composite Structures:Behaviour and Design for Fire Safety”. 1 ed. London: CRC Press. p. 352. ISBN: 9780429257056. DOI: https://doi.org/10.1201/9781482267693