Pesquisa Aplicada

https://doi.org/10.21041/ra.v10i1.448

Análise numérica das características da seção de lajes mistas de aço e concreto em situação de incêndio

Numerical analysis of composite concrete and steel slabs section under fire situation

Análisis numérico de la sección de losas de hormigón compuesto y acero bajo incendio

F. Barcellos¹ , F. Bolina² , B. Tutikian^{2 *}

¹ Master student in Graduate Program of Architecture and Urbanism, Universidade do Vale do Rio dos Sinos, São Leopoldo, Brazil.

^² itt Performance, Universidade do Vale do Rio dos Sinos, São Leopoldo, Brazil. .

^* Autor de Contato: btutikian@terra.com.br

Recepção: 29 de julho de 2019.
Aceitação: 11 de dezembro de 2019.
Publicação: 31 de dezembro de 2019.

Citar como: Barcellos, F., Bolina, F., Tutikian, B. (2020), "Análise numérica das características da seção de lajes mistas de aço e concreto em situação de incêndio", Revista ALCONPAT, 10 (1), pp. 69 – 78, DOI: https://doi.org/10.21041/ra.v10i1.448

RESUMO
Este trabalho busca avaliar o desempenho de lajes mistas de aço e concreto em situação de incêndio, correlacionando-as ao projeto em temperatura ambiente, conforme NBR 14323 (ABNT, 2013), NBR 8800 (ABNT, 2008) e NBR 14762 (ABNT, 2010), através da curva de aquecimento da ISO 834 (ISO, 1999) e distribuição de temperaturas obtidas segundo o software Ansys. Os modelos computacionais foram calibrados pela norma e extrapolados computacionalmente. Foram analisadas lajes com chapas trapezoidais de diferentes geometrias e com camadas de concreto variadas. Como resultados, as chapas com reentrâncias apresentaram melhor desempenho face às trapezoidais, sendo a espessura da camada de concreto preponderante no comportamento destas lajes ao incêndio, visto a sua maior estabilidade térmica.
Palavras-chave: segurança contra incêndio, lajes mistas, aço, concreto

ABSTRACT
This work aims to evaluate the performance of composite slabs under fire, correlating them to the project at normal temperature, according to NBR 14323 (ABNT, 2013), NBR 8800 (ABNT, 2008) and NBR 14762 (ABNT, 2010). ), through the heating curve of ISO 834 (ISO, 1999) and distribution of slab temperatures obtained by using Ansys software. The computational models were calibrated according to the standard and extrapolated to other design scenarios, with different geometries, thicknesses and effective thicknesses of the concrete layer. As results, the steel deck with recesses had better performance in relation to the trapezoids, being the thickness of the concrete layer the preponderant variable in the behavior of these slabs at high temperatures, due to their greater thermal stability.
Keywords: fire safety, composite slabs, steel, concrete

RESUMEN
Este trabajo tiene como objetivo evaluar el rendimiento de las losas compuestas bajo fuego, correlacionándolas con el proyecto a temperatura normal, de acuerdo con NBR 14323 (ABNT, 2013), NBR 8800 (ABNT, 2008) y NBR 14762 (ABNT, 2010), a través de la curva de calentamiento de ISO 834 (ISO, 1999) y la distribución de las temperaturas de losas obtenidas utilizando el software Ansys. Los modelos computacionales fueron calibrados de acuerdo con el estándar y extrapolados a otros escenarios de diseño, con diferentes geometrías, espesores y espesores efectivos de la capa de concreto. Como resultado, la plataforma con rebajes tuvo un mejor rendimiento en relación con los trapecios, siendo el espesor de la capa de hormigón la variable preponderante en el comportamiento de estas losas a altas temperaturas, debido a su mayor estabilidad térmica.
Palabras clave: seguridad contra incendios, losas compuestas, acero, hormigón.

1. IntroduÇÃo

As lajes mistas de aço e concreto possuem algumas vantagens construtivas em comparação a sistemas tradicionais. Elas oferecem uma plataforma de trabalho durante a execução da estrutura, velocidade de construção, aumento da estabilidade local e global da estrutura de aço, redução da altura das vigas e do peso próprio da estrutura (Craveiro, 2010; Liang, 2015). Apesar de ser uma solução bastante empregada, sua sensibilidade ao fogo do aço exige maior atenção em projeto (Li; Wang, 2013). A sensibilidade dos materiais metálicos a altas temperaturas fundamenta esta discussão. No caso destas lajes, a esbeltez da chapa perfilada incorporada pode promover rápida falência e ruptura brusca, como citado por (Li et.al., 2017).

As análises de estruturas mistas em altas temperaturas elaborados no Building Research Establisment na década de 90, em Cardington, na Inglaterra, motivados por incêndios em edifícios altos, como do One Meridian Plaza, nos Estados Unidos (1991), e BroadGate, na Inglaterra (1990), mostraram um desempenho superior ao esperado das lajes mistas, que não apresentaram colapso (Selamet; Bolukbas, 2016). A sua iteração com a viga e sua redistribuição de esforços promoveram a mobilização do efeito de membrana (Nguyen et.al., 2015), que melhorou sua resistência ao fogo. Discussões sobre o conservadorismo das normas eclodiram (Bailey et.al., 2000), face ao fenômeno notado - de difícil predição à nível de projeto (Gillie et.al., 2001) - que demonstrou que estruturas metálicas possuíam uma resistência ao fogo inerente, não identificadas em simulações e/ou verificações numéricas (Omer et.al., 2009).

Nos estudos feitos em Cardington, no Reino Unido, foi constatado que a geometria da chapa de aço tem papel importante na distribuição da temperatura na laje, influenciando sua resistência ao fogo (Li et al2017). A nervura da chapa faz com que a umidade do concreto neste local demore mais a evaporar, diminuindo a temperatura geral do concreto. A espessura da chapa de aço, por sua vez, não influencia na distribuição da temperatura na laje, uma vez que sua pequena dimensão faz com que a sua temperatura média seja praticamente igual em todos os casos, com valores médios semelhantes (Li, Wang, 2013).

O concreto também tem grande influência sobre o comportamento das lajes mistas expostas a incêndios. Devido sua baixa condutividade térmica, quanto maior a espessura de sua camada, menor é consequência das altas temperaturas na laje, que apresenta uma maior resistência ao fogo (Li, Wang, 2013). Ainda, o efeito de membrana se torna mais desenvolvido nestes casos. O desplacamento do concreto tende a ser mitigado nestas lajes, haja visto a barreira propiciada pela chapa perfilada (Costa et al, 2002; Wang, 2002).

A verificação de estruturas mistas de aço e concreto em situação de incêndio é feito pela NBR 14323 (ABNT 2013), com forte inspiração no EN 1994-1-2 (EN, 2005). Ela especifica que o projeto destas estruturas em alta temperatura deve ser feito no Estado Limite Último (ELU), não sendo necessária verificação no Estado Limite de Serviço (ELS). A norma propõe que o dimensionamento pode ser feito através do resultado de ensaios ou por métodos analíticos de cálculo.

A verificação estrutural das lajes em altas temperaturas passa por três critérios: estanqueidade, isolamento térmico e capacidade resistente, sendo que a NBR 14323 (ABNT 2013) considera o critério de estanqueidade atendido com a presença da chapa de aço. O critério do isolamento térmico é determinado pela espessura efetiva da laje. Sua capacidade resistente é determinada através de análise plástica global, considerando os momentos positivos e negativos gerados pelo carregamento especificado e obtidos através do diagrama de momentos fletores.

Segundo a norma, a contribuição proporcionada pela chapa de aço no momento resistente é calculada pelo somatório da contribuição de cada elemento que compõe a chapa, conforme Equação 1, sendo A_efi a área efetiva da parte i em cm², d_i a distância do centro de gravidade da parte i até a linha neutra da seção da laje em cm, f_yk a resistência ao escoamento do aço utilizado em kN/cm² e k_{y,θ i} o coeficiente de redução da resistência do aço conforme a temperatura indicada para aquele elemento, que é calculada através de coeficientes indicados na norma para o tempo requerido de resistência ao fogo (TRRF) de 60, 90 e 120 minutos. Para o cálculo da posição linha neutra em relação à face superior da laje é utilizada a Equação 2, onde f _{c k} é a resistência à compressão do concreto em kN/cm², k_c,θ é o coeficiente de redução da resistência do concreto conforme a temperatura e b_w é a largura da laje.

(1)

(2)

A contribuição proporcionada pelo concreto é calculada conforme a Equação 3, sendo que A_{e f,c} é a área de contribuição do concreto acima da linha neutra em cm², d é a distância do centro de gravidade da área comprimida do concreto até a linha neutra em cm, f_ck é a resistência à compressão do concreto em kN/cm² e k_c,θ é o coeficiente de redução da resistência do concreto conforme a temperatura, sendo indicado em norma para TRRF de 60, 90 e 120 minutos.

(3)

O momento resistente final da laje é a calculado como a soma dos momentos resistentes da chapa de aço e do concreto. O cálculo do cisalhamento não é considerado por esta norma, motivo pelo qual não será realizada a sua avaliação neste trabalho.

Apesar dos estudos que constatam a importância da geometria e espessura da chapa de aço (Li et.al., 2017; Li, Wang, 2013), e de existirem comercialmente diversas geometrias e espessuras disponíveis, as mesmas não são levadas em consideração no isolamento térmico, senão a espessura efetiva mínima da camada de concreto, conforme a NBR 14323 (ABNT 2013), merecendo, portanto, maior investigação.

Portanto, este trabalho visa analisar o comportamento de lajes mistas de aço e concreto em situação de incêndio, abordando a influência da geometria e da espessura da chapa de aço e da espessura da camada de concreto no tempo de resistência ao fogo da laje, calculando a temperatura da mesma de forma computacional segundo o Ansys, tomando como base os critérios de dimensionamento e de verificação de normas brasileiras e europeias.

2. MÉtodo

A verificação numérica foi feita com base nas equações da NBR 8800 (ABNT, 2008), NBR 14323 (ABNT, 2013), NBR 15200 (ABNT, 2012) e Eurocodes correspondentes, como EN 1992 (CEN, 2010), EN 1994 (CEN, 2004). Como a NBR 14323 (ABNT, 2013) apresenta orientações limitadas de projeto para diferentes TRRF, foi necessário realizar uma análise computacional para extrapolação dos resultados, através do software Ansys, utilizando a curva de incêndio padrão definida pela ISO 834 (ISO, 1999), conforme requerido pela NBR 14323 (ABNT, 2013) para análises destas estruturas em altas temperaturas.

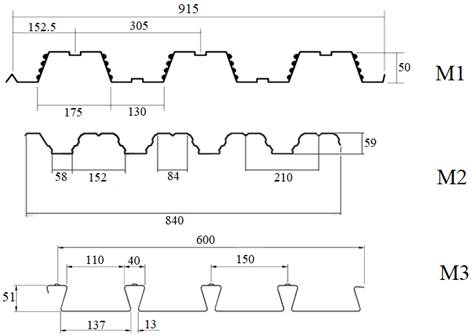
As variáveis de resposta propostas são a espessura da camada de concreto, a geometria e espessura da chapa. A avaliação foi feita de forma a explorar os valores de uma variável enquanto as outras duas tem seus valores fixos. Foram avaliadas espessuras efetivas de concreto de 80 mm, 90 mm, 100 mm, 110 mm, 120 mm, 130 mm, 140 mm e 150 mm. Entre as geometrias das chapas estudadas, foram escolhidas duas trapezoidais e uma com reentrâncias, conforme Figura 1 e as espessuras de chapas estudadas foram de 0,80 mm, 0,95 mm e 1,25 mm.

Figura 1. Modelos de chapa estudados (em mm).

Para denominação dos modelos estudados, foi escolhida a ordem da nomenclatura, sendo que o primeiro é a letra M seguido do número de modelo de chapa, depois a letra F seguida da espessura da chapa e por último a letra C seguida da espessura efetiva do concreto em milímetros. A Figura 2 mostra um exemplo da montagem da nomenclatura utilizada neste trabalho.

Figura 2. Nomenclatura dos modelos estudados

Como variáveis de controle, para análise das lajes consentidas neste estudo, foram adotados os valores do aço e do concreto em altas temperaturas, conforme apresentados na Tabela 1. O modelo de laje estudado é unidirecional e bi-apoiado, formando elementos isostáticos, de largura 1 m e vão de 3 m. Os apoios foram considerados perpendiculares às nervuras. Não há formação de forças de compressão do efeito membrana devido à vinculação do modelo, que, por ser apoiado, não restringe a movimentação horizontal. Também não foi considerada a análise construtiva para lajes mistas, pois a chapa deve suportar a totalidade das cargas durante o processo de cura do concreto. Não foi considerada a utilização de armaduras de flexão negativa nos modelos adotados, e a armadura positiva foi constituída pela chapa perfilada de aço, sendo que o colapso do modelo estudado se dá por rótula plástica sob momento positivo na seção central.

Tabela 1. Propriedades do aço e do concreto em altas temperaturas
	Propriedades do aço	Propriedades do concreto
Resistência Característica	Escoamento - Conforme Tabela 1 da NBR 14323 (ABNT, 2013)	Conforme Tabela 1 da NBR 15200 (ABNT, 2012)
Coeficiente de Poisson	0,3	0,15
Módulo de Elasticidade	Conforme Tabela 1 da NBR 14323 (ABNT, 2013)	Conforme EN 1994-1-2 (EN, 2005)
Condutividade térmica	Conforme item E.4 do Anexo E da NBR 14323 (ABNT, 2013)	Conforme item C.3 do Anexo C da NBR 15200 (ABNT, 2012)
Calor específico	Conforme item E.43 do Anexo E da NBR 14323 (ABNT, 2013)	Conforme item C.2 do Anexo C da NBR 15200 (ABNT, 2012)
Massa específica	7850 kg/m³	2500 kg/m³

Os TRRF estudados foram de 15, 30, 45, 60, 90, 120, 150 e 180 minutos. Como a NBR 14323 (ABNT, 2013) fornece os coeficientes para cálculo da temperatura da chapa de aço somente para os TRRF de 60min, 90min e 120min, foi utilizado o software Ansys para obtenção da temperatura dos elementos os TRRF não abrangidos pela norma, calibrando as extrapolações com os valores apresentados por norma.

O Ansys utiliza o método dos elementos finitos em sua análise, com a formação de malhas e análise de seus pontos de interseção. A ferramenta foi empregada para analisar a distribuição de temperatura na seção, exposta à curva padronizada de incêndio da ISO 834 (ISO, 1999). O coeficiente de convecção utilizado foi de 25 W/m².K. Não foi considerada a emissividade térmica dos materiais. A coleta da temperatura foi feita através da ferramenta Temperature Probe do Ansys. Para medir a temperatura da chapa perfilada, foram selecionadas faces expostas ao fogo, adotando como ponto de medida o plano médio do respectivo elemento que compõe a chapa. Na medição das temperaturas do concreto foi admitida a parcela comprimida da seção.

3. Resultados

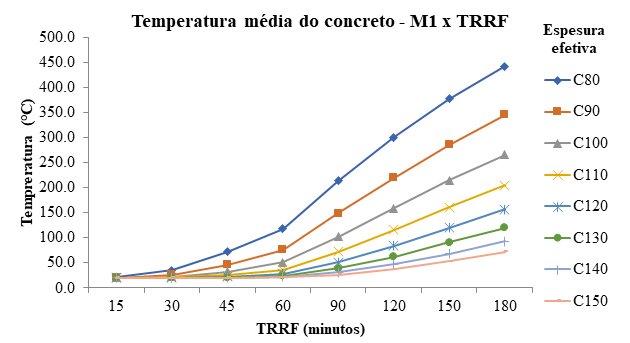
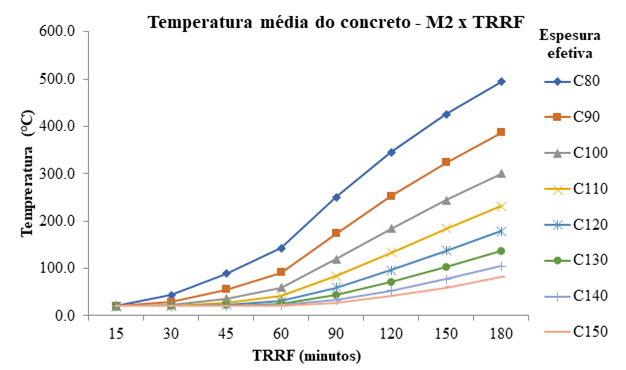
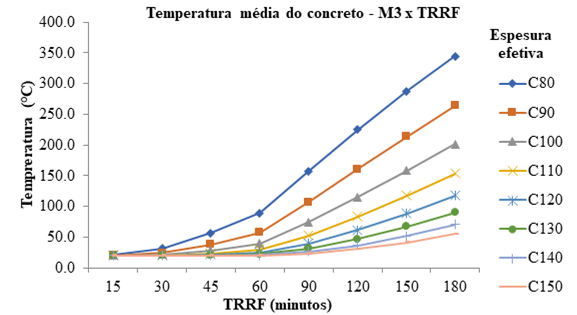
As Figura 3, Figura 4 e Figura 5 mostram a temperatura média da face superior do concreto, acima da linha neutra.

Figura 3. Temperatura média concreto com chapa M1

Figura 4. Temperatura média concreto com chapa M2

Figura 5. Temperatura média concreto com chapa M3

Percebe-se que, somente aos 60 min de exposição, a variação de temperatura é maior e mais significativa nas quatro primeiras espessuras, ultrapassando 100°C e comprometendo sua resistência. Aos 180 min, somente o modelo M1 com espessuras de 14 e 15 cm, o modelo M2 com espessura de 15 cm e o modelo M3 com espessuras de 13 a 15 cm não atingiram 100°C. Nas demais espessuras, as temperaturas chegaram a 494,5°C, tendo um coeficiente de redução de 0,61. Este comportamento de isolamento térmico do concreto pode ser explicado pela sua baixa condutividade térmica e alto calor específico, o que faz com que em face de uma exposição ao fogo necessite de alta temperatura e duração para que o calor seja transferido ao longo de sua espessura. Analisando a temperatura da chapa quando verificada a sua geometria na exposição a altas temperaturas, são obtidas temperaturas muito semelhantes para a mesa inferior e alma, o que era de se esperar, haja vista a elevada condutividade térmica do aço.

São apresentados, nas Tabelas 2, 3 e 4, os fatores de redução de resistência ao escoamento das diferentes partes da chapa. A geometria de chapa do modelo M3 tem a maior variação de temperatura nos elementos, apresentando as menores temperaturas de mesa superior e as maiores temperaturas de mesa inferior e alma entre os modelos estudados. Como consequência, estas chapas possuem maiores fatores de redução na mesa superior e os menores na mesa inferior e alma. Esta variação fica dentro de uma faixa de 133°C e é influenciada pela área e forma de exposição da mesma, que, por causa do modelo com reentrâncias, acaba isolando a mesa superior e deixando uma área maior de exposição na mesa inferior, que é transferida para a alma.

Tabela 2. Fator de redução de resistência ao escoamento da mesa superior
Modelo	15 min	30 min	45 min	60 min	90 min	120 min	150 min	180 min
M1	1,00	0,72	0,42	0,25	0,12	0,08	0,06	0,05
M2	1,00	0,79	0,47	0,30	0,15	0,09	0,08	0,07
M3	1,00	0,89	0,64	0,43	0,22	0,13	0,10	0,09

Tabela 3. Fator de redução de resistência ao escoamento da mesa inferior
Modelo	15 min	30 min	45 min	60 min	90 min	120 min	150 min	180 min
M1	1,00	0,65	0,34	0,20	0,09	0,06	0,05	0,04
M2	1,00	0,61	0,28	0,16	0,08	0,05	0,05	0,05
M3	1,00	0,52	0,24	0,14	0,07	0,05	0,05	0,04

Tabela 4. Fator de redução de resistência ao escoamento da alma
Modelo	15 min	30 min	45 min	60 min	90 min	120 min	150 min	180 min
M1	1,00	0,65	0,34	0,20	0,09	0,06	0,05	0,04
M2	1,00	0,61	0,28	0,16	0,08	0,05	0,05	0,05
M3	1,00	0,52	0,24	0,14	0,07	0,05	0,05	0,04

A temperatura da chapa não sofreu variação significativa com a mudança de espessura, atribuído a elevada condutividade térmica do aço e as dimensões reduzidas da espessura da chapa. No modelo de cálculo da NBR 14323 (ABNT, 2013), somente a geometria do modelo de chapa influencia na variação da temperatura, sendo que ela é igual para todas as espessuras de um mesmo modelo. Este procedimento foi confirmado com a verificação no Ansys, pois a variação não ultrapassou 1% entre espessuras.

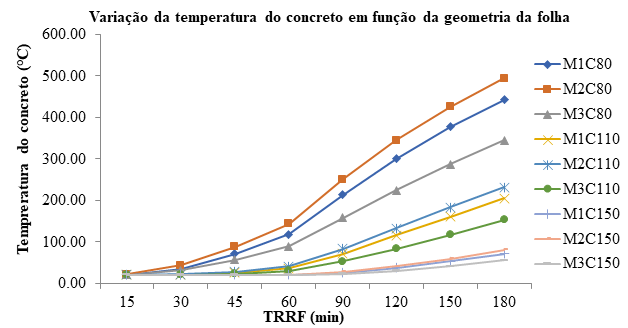
Correlacionando as variáveis que influenciam na resistência da laje em altas temperaturas (geometria da chapa e a espessura da camada de concreto) e fazendo uma média em função destes valores com a espessura da chapa, pode-se afirmar que as diferenças de temperatura em função da geometria são mais significativas nas menores espessuras de concreto, diminuindo conforme o aumento da espessura, conforme ilustrado na Figura 6. Apesar disto, sempre se observou a vantagem do modelo M3 em relação aos outros modelos. Com o aumento do TRRF, a diferença de temperatura relativa à espessura da camada de concreto foi diminuindo.

Figura 6. Variação da temperatura do concreto em função da geometria da chapa

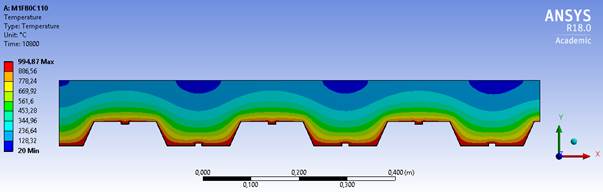
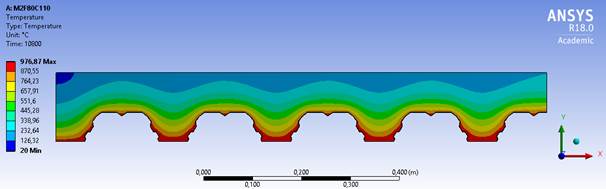
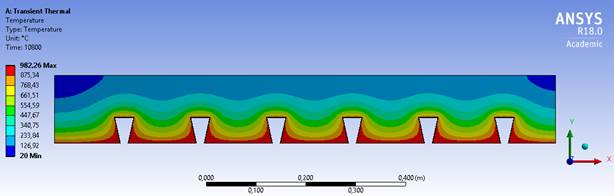
O modelo M1 apresenta uma geometria semelhante ao modelo M2 conforme mostram as Figuras 7 e 8, o que faz com que a variação de temperatura entre estes dois modelos seja menor. A variação mais significativa é entre a geometria do modelo M2 e do modelo M3, sendo que o primeiro tem sempre a maior temperatura e o segundo a menor temperatura entre os modelos estudados. Isto se deve ao fato de que a geometria do modelo M2 expõe mais a sua mesa superior, facilitando com que a temperatura atinja valores mais altos no concreto. A geometria do modelo M3 é com reentrâncias, o que permite que o calor se concentre na mesa inferior da chapa e dificulte o acesso do ar quente na mesa superior, conforme mostra a Figura 9. As isotermas mostram também a forma como a temperatura avança nas lajes, sendo que no modelo M3 elas se comportam de forma constante, formando linhas retas, enquanto nos outros dois modelos elas formam ondas.

Figura 7. M1F80C110 com TRRF de 180 minutos

Figura 8. M2F80C110 com TRRF de 180 minutos

Figura 9. M3F80C110 com TRRF de 180 minutos

A variável que mais influenciou a temperatura foi a geometria da folha de aço, com o modelo M3, com reentrâncias, tendo o melhor desempenho entre os estudados. Isto se deveu a maior área de aço unitária destes elementos e maior consumo de concreto - de maior estabilidade térmica - nas nervuras.

A espessura efetiva da camada de concreto também se mostrou influente. Pelo concreto ter condutividade térmica baixa, quanto maior sua espessura menor foi a temperatura da parcela resistente à compressão da laje, local onde o concreto efetivamente atua no momento resistente. O inconveniente desta solução é o aumento do peso da estrutura.

A partir dos 30 minutos de exposição ao incêndio, o coeficiente de redução da folha de aço mostra que a mesma não tem mais participação estrutural, deixando o concreto não armado submetido à flexão. Sendo assim, nas análises numéricas concebidas com base nas equações normativas, é necessária a utilização de armadura positiva para evitar a ruptura brusca do concreto em altas temperaturas. Todavia, os estudos experimentais têm nos mostrado que estas lajes possuem uma resistência ao fogo intrínseca, haja visto o efeito de membrana que se forma, difícil de ser previsto numericamente.

4. ConclusÕes

Entre os itens avaliados neste trabalho, os que exercem maior influência sobre o comportamento de lajes mistas de concreto e aço são a geometria da folha de aço e a espessura da camada de concreto, respectivamente. Isto ocorre devido principalmente a estabilidade térmica gerada pela geometria que permite um maior consumo de concreto e a baixa condutividade térmica do concreto.

ReferÊncias

Associação Brasileira de Normas Técnicas (2013). NBR 14323: Projeto de estruturas de aço e de estruturas mistas de aço e concreto de edifícios em situação de incêndio. Rio de Janeiro.

Associação Brasileira de Normas Técnicas (2008). NBR 8800: Projeto de Estruturas De Aço e de estruturas mistas de aço e concreto de edifícios. Rio de Janeiro.

Associação Brasileira de Normas Técnicas (2010). NBR 14762: Dimensionamento de estruturas de aço constituídas por perfis formados a frio. Rio de Janeiro.

Associação Brasileira de Normas Técnicas (2012). NBR 15200: Projeto de estruturas de concreto em situação de incêndio. Rio de Janeiro.

Bailey, C. G.; White, D. S.; Moore, D. B. (2000). The tensile membrane action of unrestrained composite slabs simulated under fire conditions. Engineering Structures. 22 (12):1583-1595. https://doi.org/10.1016/S0141-0296(99)00110-8

Costa, C. N.; Figueiredo, A. D.; Pignatta, V. (2002). O fenômeno do lascamento (“spalling”) nas estruturas de concreto armado submetidas a incêndio - uma revisão crítica. In: In: 44º Congresso Brasileiro do Concreto- IBRACON 2002. Anais eletrônicos. Belo Horizonte.

Craveiro, H. D. S. (2010). “Análise do comportamento estrutural de lajes mistas aço-betão com reforço transversal”. Dissertação de mestrado. Universidade de Coimbra, Coimbra.

European Committee for Standardization (2005). EN 1994-1-2: Design of composite steel and concrete structures - Part 1-2: General rules - structural fire design: Eurocode 4. Brussels.

Gillie, M.; Usmani, A. S.; Rotter, J. M. (2001). A structural analysis of the first Cardington test. Journal of Constructional Steel Research. 57 (6):581-601. https://doi.org/10.1016/S0143-974X(01)00004-9

Li, G.; Zhang, N.; Jiang, J. (2017). Experimental investigation on thermal and mechanical behaviour of composite floors exposed to standard fire. Fire Safety Journal. 89:63-76. https://doi.org/10.1016/j.firesaf.2017.02.009

Liang, Q. Q. (2015). “Analysis and Design of Steel and Composite Structures”. CRC Press, New York. p. 458. ISBN: 9780415532204

Li, G.; Wang, P. (2013). “Advanced Analysis and Design for Fire Safety of Steel Structures”. China: Zhejiang University Press, Springer-Verlag Berlin Heidelberg. p. 357. ISBN: 9783642343933

Nguyen, T. T.; Tan, K. H.; Burgess, I. W. (2015). Behaviour of composite slab-beam systems at elevated temperatures: Experimental and numerical investigation. Engineering Structures, 82: 199-213. https://doi.org/10.1016/j.engstruct.2014.10.044

Omer, E.; Izzuddin, B. A.; Elghazouli, A. Y. (2009). Failure of lightly reinforced concrete floor slabs with planar edge restraints under fire. Journal of Structural Engineering, 135 (9): 1068-1080. https://doi.org/10.1061/(ASCE)0733-9445(2009)135:9(1068)

Selamet, S.; Bolukbas, C. (2016). Fire resilience of shear connections in a composite floor: Numerical investigation. Fire Safety Journal, 81: 97-108. https://doi.org/10.1016/j.firesaf.2016.02.003

Vargas, M. R.; Silva, V. P. (2005). Resistência ao fogo das estruturas de aço. Rio de Janeiro: IBS/CBCA. Rio de Janeiro. P.78. ISBN: 85-89819-02-7.

Wang, Y. C. (Ed.). (2002). “Steel and Composite Structures:Behaviour and Design for Fire Safety”. 1 ed. London: CRC Press. p. 352. ISBN: 9780429257056. DOI: https://doi.org/10.1201/9781482267693