Pesquisa Básica

Um modelo analítico para projeto de sapata de canto combinadas

An analytical model for the design of corner combined footings

Un modelo analítico para el diseño de zapatas combinadas de esquina

A. Luévanos Rojas¹ ^* , S. López Chavarría¹ , M. Medina Elizondo¹ , R. Sandoval Rivas¹ , O. M. Farías Montemayor¹ ,

¹ Instituto de Investigaciones Multidisciplinarias, Universidad Autónoma de Coahuila, Torreón, Coahuila, México. .

^*Autor de Contato: arnulfol_2007@hotmail.com

Recepção: 24 de agosto de 2019.
Aceitação: 06 de abril de 2020.
Publicação: 01 de setembro de 2020.

Citar como: Luévanos Rojas, A., López Chavarría, S., Medina Elizondo, M., Sandoval Rivas, R., Farías Montemayor, O. M. (2020), "Um modelo analítico para projeto de sapata de canto combinadas", Revista ALCONPAT, 10 (3), pp. 317 – 335, DOI: https://doi.org/10.21041/ra.v10i3.432

Resumo
Este trabalho apresenta um modelo analítico para o dimensionamento de sapatas angulares combinadas submetidas a uma carga axial e dois momentos fletores ortogonais para cada pilar que leva em consideração a pressão real do solo sob a sapata, e a metodologia é baseada no princípio de que a integração da força cortante é o momento. O projeto atual considera a pressão máxima em todos os pontos de contato. Este modelo é verificado pelo equilíbrio das forças de cisalhamento e momentos. A aplicação do modelo é apresentada por meio de um exemplo numérico. Portanto, o modelo proposto é o mais adequado, pois gera um melhor controle de qualidade dos recursos utilizados.
Palavras-chave: sapatas combinadas de canto, modelo analítico para projeto, momentos de flexão, cisalhamento por flexão, cisalhamento por punção.

Abstract
This work shows an analytical model for the design of corner combined footings subjected to an axial load and two orthogonal flexural moments per each column. It considers the real pressure on the ground below of the footing, and the methodology is based on the principle that the integration of the shear force is the moment. The current design considers the maximum pressure at all contact points. This model is verified by equilibrium of shear forces and moments. The application of the model is presented by means of a numerical example. Therefore, the proposed model is the most appropriated, because it generates better quality control in the resources used.
Keywords: corner combined footings, analytical model for design, flexural moments, flexural shearing, punching shearing.

Resumen
Este trabajo muestra un modelo analítico para el diseño de zapatas combinadas de esquina sometidas a una carga axial y dos momentos flexionantes ortogonales por cada columna. El modelo toma en cuenta la presión real del suelo debajo de la zapata, y la metodología se basa en el principio de que la integración de la fuerza de corte es el momento. El diseño actual considera la presión máxima en todos los puntos de contacto. Este modelo se verifica por equilibrio de fuerzas de corte y momentos. La aplicación del modelo se presenta por medio de un ejemplo numérico. Por lo tanto, el modelo propuesto es el más apropiado, ya que genera un mejor control de calidad en los recursos utilizados.
Palabras clave: zapatas combinadas de esquina, modelo analítico para diseño, momentos flexionantes, cortante por flexión, cortante por penetración.

1. IntroduÇÃo

Uma fundação ou mais comumente chamada de base que é o elemento de uma estrutura arquitetônica que a conecta ao solo e que transfere as cargas da estrutura para o solo. As fundações são divididas em dois tipos, rasas e profundas (Bowles, 2001; Das et al., 2006).

As fundações rasas para pilares são de cinco tipos principais: 1) sapatas corridas; 2) sapatas isoladas; 3) sapatas combinadas suportando dois ou mais pilares; 4) sapatas de cintamento ou de balanço; 5) lajes de fundação ou radier que cobrem toda a área de fundação (Bowles, 2001).

Uma sapata combinada é necessária para apoiar um pilar que está localizada muito perto do limite da propriedade, de modo a não invadir a propriedade adjacente. A base combinada pode ser uma laje de espessura uniforme ou uma viga em T invertida. Se o tipo de laje da sapata combinada for usado para apoiar dois ou mais pilares (geralmente dois), a laje deve ter uma forma retangular, trapezoidal ou em forma de T quando um pilar está mais carregado do que o outro (Kurian, 2005; Punmia et al., 2007; Varghese, 2009).

A pressão do solo sob uma sapata depende do tipo de solo, da rigidez relativa do solo e da sapata e da profundidade da fundação ao nível de contato entre a sapata e o solo.

A Figura 1 mostra a distribuição da pressão do solo sob a sapata de acordo com o tipo de solo e a rigidez da sapata (Bowles, 2001).

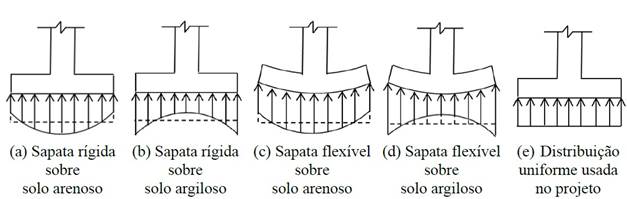
Figura 1. Pressão abaixo da sapata

Estudos sobre estruturas de fundação e modelos matemáticos para sapatas têm sido investigados com sucesso em vários problemas de engenharia geotécnica. As principais contribuições de vários pesquisadores na última década são: “Comportamento de sapatas retangulares carregadas repetidamente em areia armada” (El Sawwaf e Nazir, 2010); "Vibração não linear de placas de compósito híbrido em fundações elásticas" (Chen et al., 2011); "Tabelas de projeto estocástico para capacidade de carga da sapata" (Shahin e Cheung, 2011); “Otimização de partículas modificadas para projeto ideal de suporte estendido e muro de contenção” (Khajehzadeh et al., 2011); “Projeto de sapatas retangulares em novo modelo” (Luévanos-Rojas et al., 2013); “Projeto de sapatas circulares isoladas em novo modelo” (Luévanos-Rojas, 2014a); “Projeto de sapatas retangulares combinadas com um limite usando um novo modelo” (Luévanos-Rojas, 2014b); “Determinação dos estados limites últimos de fundações de superfície usando a abordagem de programação de expressão gênica (GEP)” (Tahmasebi poor et al., 2015); “Projeto de sapatas combinadas de aresta trapezoidal em um novo modelo” (Luévanos-Rojas, 2015); “Novo método iterativo para calcular a tensão na base da sapata sob flexão biaxial” (Aydogdu, 2016); “Um estudo comparativo para o dimensionamento de sapatas retangulares e circulares isoladas usando novos modelos” (Luévanos-Rojas, 2016a); “Influência da rigidez das sapatas na resistência à punção” (Fillo et al., 2016); "Um novo modelo para o projeto de sapatas de divisa retangulares combinadas com dois lados opostos restritos" (Luévanos-Rojas, 2016b); “Projeto estrutural de sapatas de pilares isoladas” (Abdrabbo et al., 2016); “Projeto ideal para sapatas retangulares isoladas usando pressão real do solo” (Luévanos-Rojas et al., 2017a); “Elementos finitos e análise experimental de sapatas de diferentes formatos na areia” (Anil et al., 2017); “Um estudo comparativo para o projeto de sapatas combinadas de formas trapezoidais e retangulares usando novos modelos” (Luévanos-Rojas et al., 2017b); “Desempenho de sapatas isoladas e dobradas” (El-kady e Badrawi, 2017); “Análise e projeto de vários tipos de sapatas isoladas” (Balachandar e Narendra Prasad, 2017); “Um novo modelo para sapatas combinadas em forma de T Parte II: Modelo matemático para design” (Luévanos-Rojas et al., 2018); “Resistência ao punçoamento de sapatas de concreto armado: avaliação do código de projeto” (Santos et al., 2018); “Efeito de fundações de solo na resposta à vibração de fundações de concreto usando um modelo matemático” (Dezhkam e Yaghfoori, 2018); “Análise de não linearidade no estudo de fundações de grades rasas” (Ibrahim et al., 2018); "Modelagem para sapatas combinadas Parte II: modelo matemático para projeto" (Yáñez-Palafox et al., 2019); "Método numérico para a análise e dimensionamento de sapatas quadradas isoladas sob carga concêntrica" (Magade e Ingle, 2019).

O documento relacionado a este trabalho é: "O dimensionamento ideal para sapatas de canto combinadas" para obter apenas a área mínima da superfície de contato no solo entre o solo e a sapata (López-Chavarría et al., 2017), mas este documento não apresenta o projeto de sapatas de canto combinadas (inclinação efetiva e aço de armadura).

Este documento mostra um modelo analítico para o projeto de sapatas de canto combinadas sujeitas a uma carga axial e dois momentos de flexão ortogonais para cado pilar, e a pressão do solo na sapata é apresentada como uma função dos efeitos gerados por cado pilar, e a metodologia é baseada no princípio de que a integração da força cortante é o momento. O projeto atual considera a pressão máxima em todos os pontos de contato, pois o centro de gravidade da sapata é forçado a coincidir com a posição da força resultante das cargas. Este modelo é verificado pelo equilíbrio das forças de cisalhamento e momentos. A principal vantagem do modelo proposto é apresentar o momento, o cisalhamento na flexão e a punção por meio de equações analíticas. Portanto, o modelo proposto será o mais adequado, pois gera um melhor controle de qualidade nos recursos utilizados (mão de obra, materiais, pequenos equipamentos, etc.), pois se ajusta às condições da real pressão do solo.

2. Formulação do modelo proposto

As seções críticas para sapatas de acordo com o código são (ACI 318S-14, 2014): 1) O momento está localizado na face do pilar; 2) A cortante de flexão está localizada a uma distância "d" da face do pilar; 3) O punçionamento ocorre a uma distância "d / 2" em ambas as direções.

A carga axial e dois momentos fletores ortogonais (flexão biaxial) de cada pilar aplicado na sapata de canto combinada são mostrados na Figura 2 (a). A pressão sob a sapata de canto combinada que varia linearmente, e a tensão em cada vértice da sapata é apresentada na Figura 2 (b).

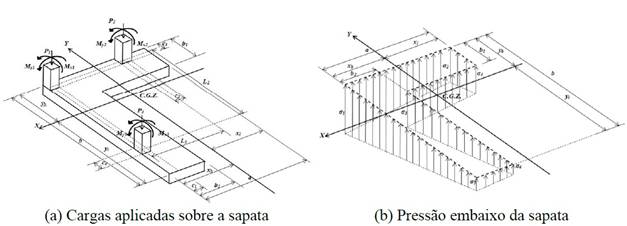
Figura 2. Sapata combinada de canto

Os esforços na direção principal (eixos "X" e "Y") são obtidos:

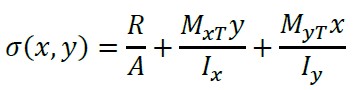
(1)

onde: R, M_xT, M_yT, A, I_x, e I_y foram obtidas de (López-Chavarría et al., 2017).

Os esforços abaixo do pilar 2 (eixos “X₂” e “Y₂”) se encontram (ver Figura 3):

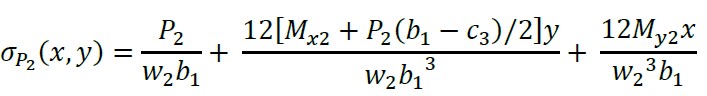
(2)

Os esforços abaixo do pilar 3 (eixos “X₃” e “Y₃”) são obtidos por (ver Figura 3):

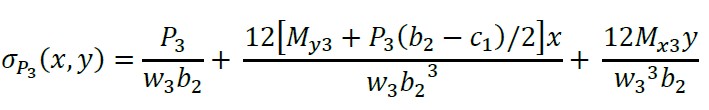
(3)

onde: w₂ e w₃ são as larguras da superfície de análise nos pilares 2 e 3: w₂ = c₂ + d, w₃ = c₄ + d.

2.1 Cortantes por flexão e momentos flexionantes

As seções críticas para momentos fletores são apresentadas nos eixos: a'-a ', b'-b', c'-c ', d'-d', e'-e ', f'-f', g ' -g ', h'-h', i'-i 'e j'-j' (consulte a Figura 3). As seções críticas para cortantes de flexão são apresentadas nos eixos: k'-k ', l'-l', m'-m ', n'-n', o'-o ', p'-p', q '-q' e r'-r '(consulte a Figura 4).

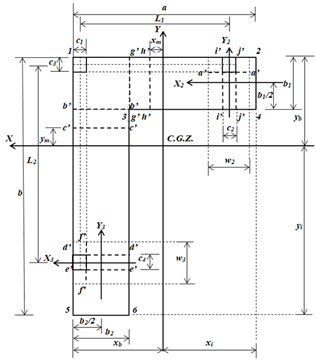
Figura 3. Seções críticas para momentos de flexão

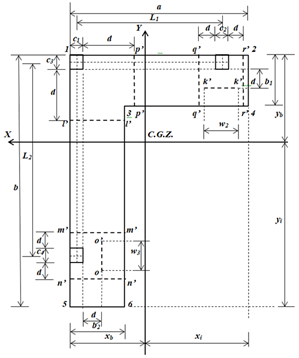
Figura 4. Seções críticas para cortantes por flexão

Nota: Quando os momentos em torno do eixo X são obtidos, os momentos em torno do eixo Y são considerados iguais a zero. Quando os momentos em torno do eixo Y são obtidos, os momentos em torno do eixo X não têm influência. Porque estes são eixos perpendiculares uns aos outros.

2.1.1 Cortantes de flexão e momentos em torno de um eixo paralelo ao eixo “X₂” de - b₁/2 ≤ y₂ ≤ b₁/2 - c₃/2

A cortante " V_y2" é encontrada através do volume de pressão da área formada pelo eixo " X₂" com largura " w₂ = c₂ + d " e a extremidade livre (lado interno) da sapata:

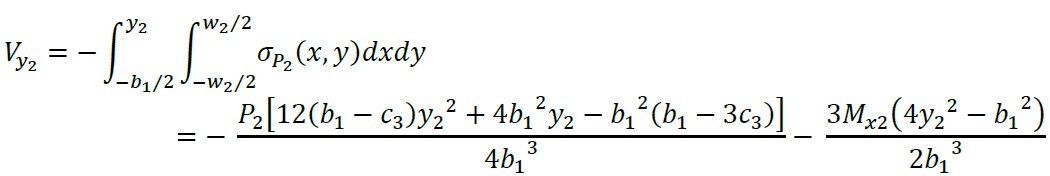
(4)

Ao integrar a equação (4) em relação a " y₂", obtém-se:

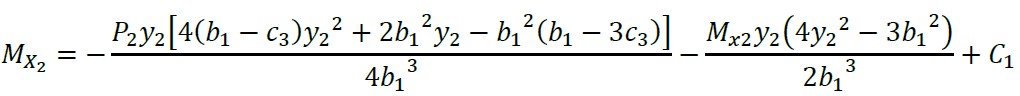
(5)

onde: M_X2 é e momento ao redor do eixo “X₂” e V_y2 é a cortante a uma distância “y₂”.

Agora, substituindo “y₂ = − b₁/2” e “M_X2 = 0” na equação (5) e a constante “C₁” é:

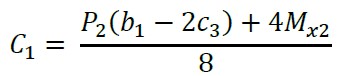
(6)

Substituindo a equação (6) na equação (5) e a equação do momento generalizado é apresentada a seguir:

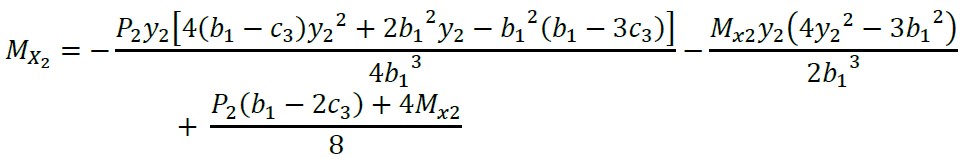
(7)

2.1.2 Cortantes por flexão e momentos sobre um eixo paralelo ao eixo “X” de y_b - c₃/2 ≤ y ≤ y_b

A cortante "V_y" é encontrada através do volume de pressão da área formada pelo eixo "X" com largura "a" e a extremidade livre (lado superior) da sapata:

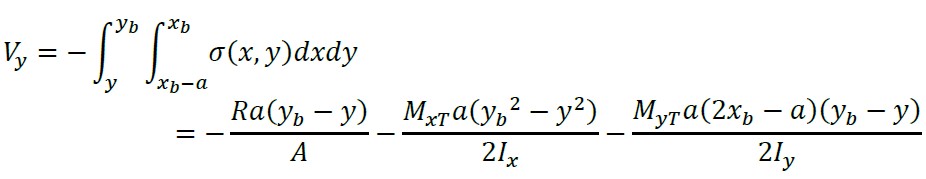
(8)

Por integração da equação (8) com respeito a "y", obtemos:

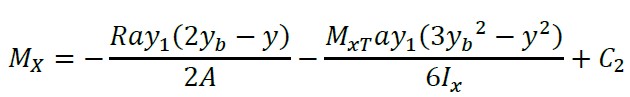
(9)

onde: M_X é o momento em torno do eixo "X" e V_y é a cortante na distância "y".

Agora, substituindo "y = y_b " e " M_X = 0" na equação (9) e a constante "C₂" é:

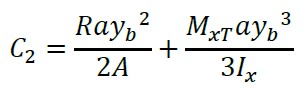
(10)

Substituindo a equação (10) na equação (9) e a equação do momento generalizado é apresentada como segue:

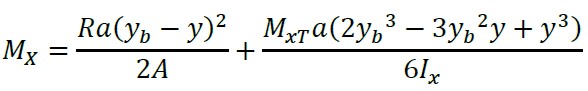
(11)

Substituindo "y = y_b − c₃/ 2" na equação (11) para obter o momento em torno do eixo localizado no centro do pilar 1 e 2 " M_c3/2":

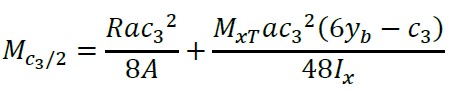
(12)

2.1.3 Cortantes por flexão e momentos sobre um eixo paralelo ao eixo “X” de y_b - b₁ ≤ y ≤ y_b - c₃/2

A cortante " V_y" é encontrada através do volume de pressão da área formada pelo eixo "X" com largura "a" e parte superior da sapata:

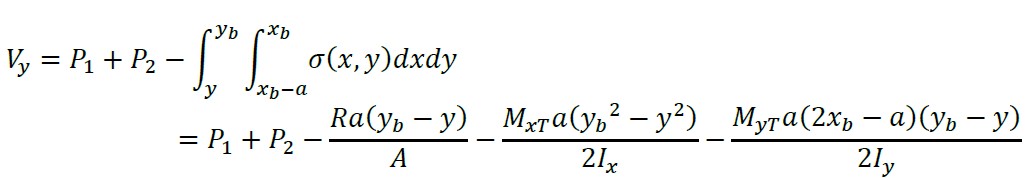
(13)

Ao integrar a equação (13) com respeito a "y", obtemos:

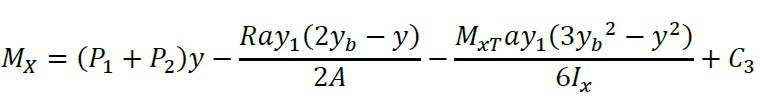
(14)

Agora, substituindo “y = y_b - c₃/2” e “M_X = M_c3/2 - M_x1 - M_x2” na equação (14) e a constante “C₃” é:

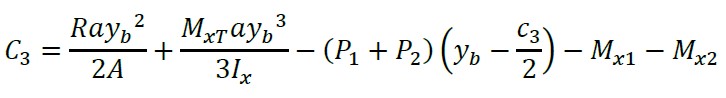
(15)

Substituindo a equação (15) na equação (14) e a equação do momento generalizado é apresentada como segue:

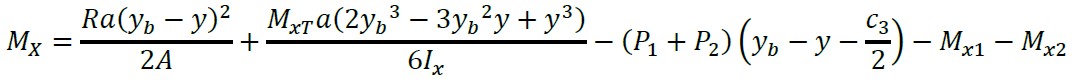
(16)

Substituindo “y = y_b - b₁” na equação (16) para obter o momento ao redor do eixo b’-b’ “M_b1”:

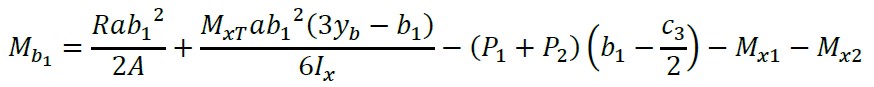
(17)

2.1.4 Cortantes por flexão e momentos sobre um eixo paralelo ao eixo “X” de y_b - L₂ - c₃/2 ≤ y ≤ y_b - b₁

A cortante “V_y” é encontrada através do volume de pressão da área formada pelo eixo “X” e a parte superior da sapata:

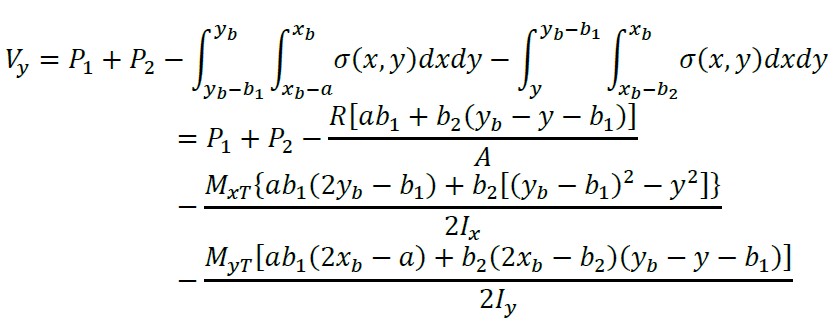
(18)

Ao integrar a equação (18) com respeito a "y", obtemos:

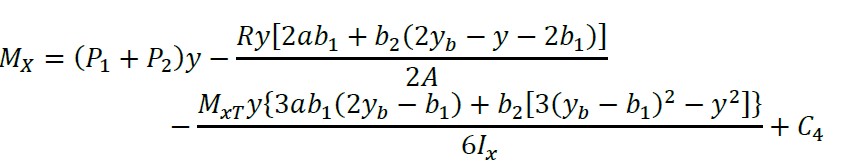
(19)

Agora, substituindo “y = y_b - b₁” e “M_X = M_b1” na equação (19) e a constante “C₄” é:

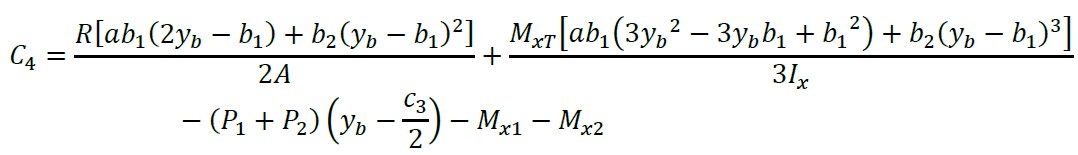
(20)

Substituindo a equação (20) na equação (19) e a equação de momentos generalizados se apresenta como segue:

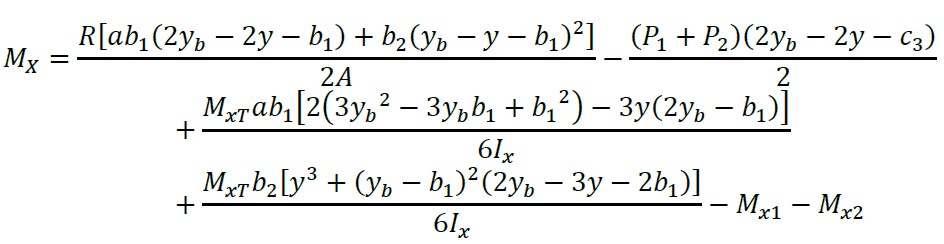
(21)

Substituindo “y = y_b - L₂ - c₃/2” na equação (21) para obter o momento ao redor do eixo localizado no centro do pilar 3 “M_L2”:

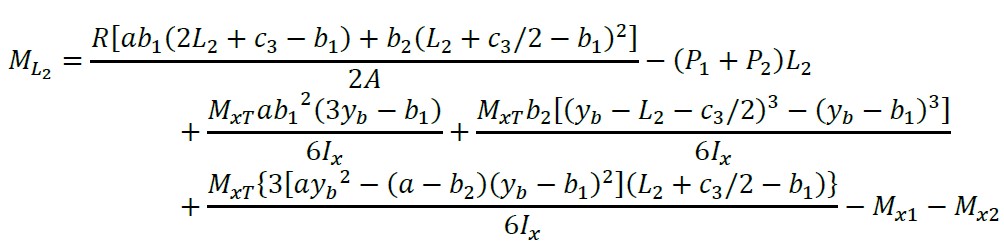
(22)

2.1.5 Cortantes por flexão e momentos sobre um eixo paralelo ao eixo “X” de y_b - b ≤ y ≤ y_b - L₂ - c₃/2

A cortante “V_y” pode ser encontrada através do volume de pressão da área formada pelo eixo “X” e a parte de cima da sapata:

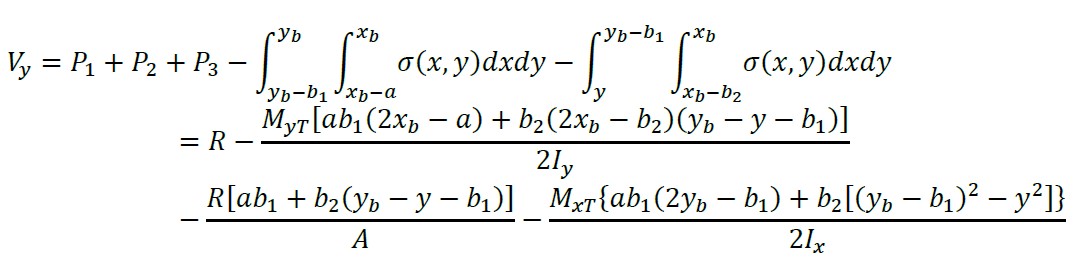
(23)

Pela integração da equação (23), obtem-se:

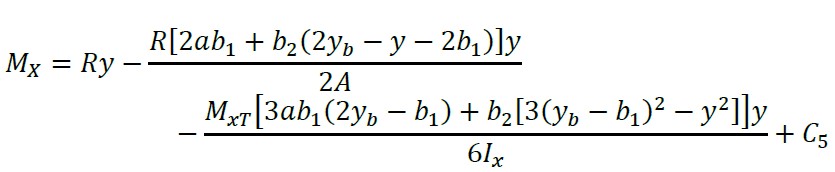
(24)

Agora, substituindo “y = y_b - L₂ - c₃/2” e “M_X = M_L2 - M_x3” e a constante “C₅” é:

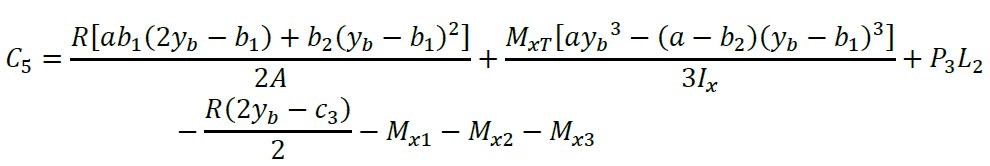
(25)

Substituindo a equação (25) na equação (24) e a equação dos momentos fletores generalizados é apresentada a seguir:

(26)

Nas seções seguintes, para obter as equações da cortante e dos momentos generalizados, é utilizado o mesmo procedimento utilizado anteriormente. Portanto, as equações para as cortantes de flexão e momentos generalizados são mostradas abaixo.

2.1.6 Cortantes por flexão e momentos sobre um eixo paralelo ao eixo “Y₃” de - b₂/2 ≤ x₃ ≤ b₂/2 - c₁/2

(27)

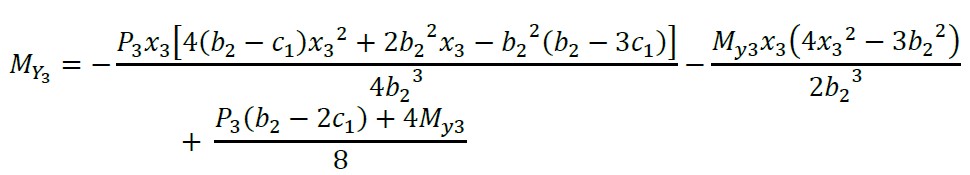
(28)

2.1.7 Cortantes por flexão e momentos sobre um eixo paralelo ao eixo “Y” de x_b - c₁/2 ≤ x ≤ x_b

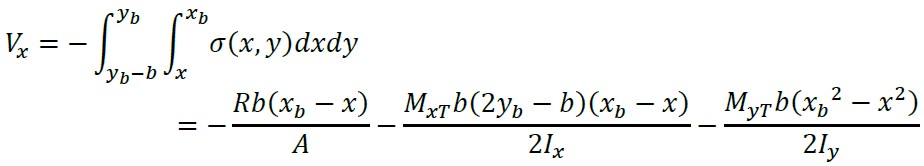
(29)

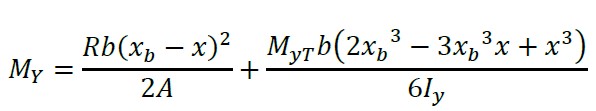
(30)

2.1.8 Cortantes por flexão e momentos sobre um eixo paralelo ao eixo “Y” de x_b - b₂ ≤ x ≤ x_b - c₁/2

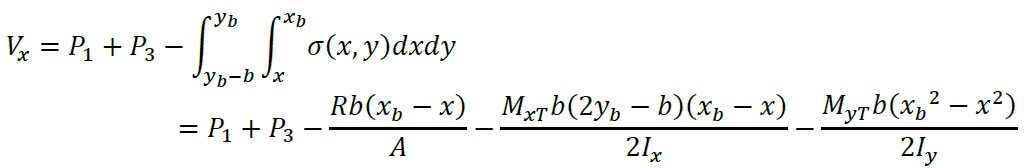
(31)

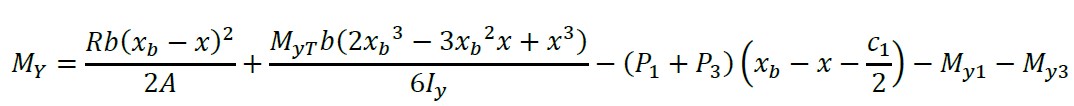
(32)

2.1.9 Cortantes por flexão e momentos sobre um eixo paralelo ao eixo “Y” de x_b - L₁ - c₁/2 ≤ x ≤ x_b - b₂

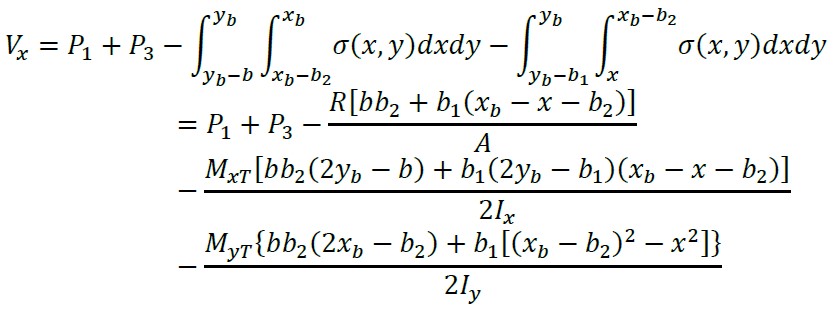
(33)

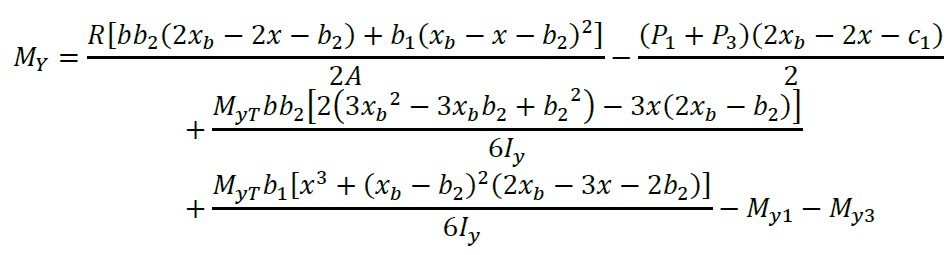
(34)

2.1.10 Cortantes por flexão e momentos sobre um eixo paralelo ao eixo “Y” de x_b - a ≤ x ≤ x_b - L₁ - c₁/2

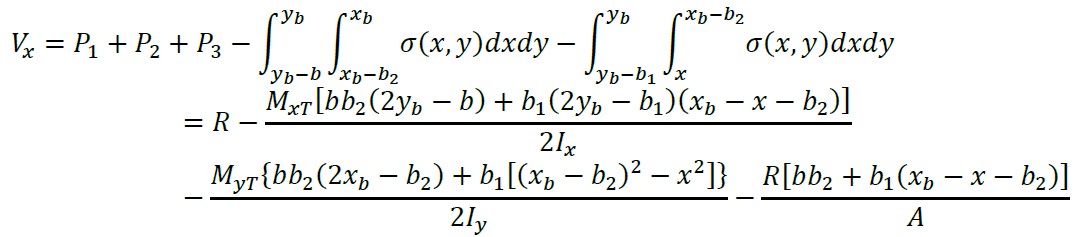
(35)

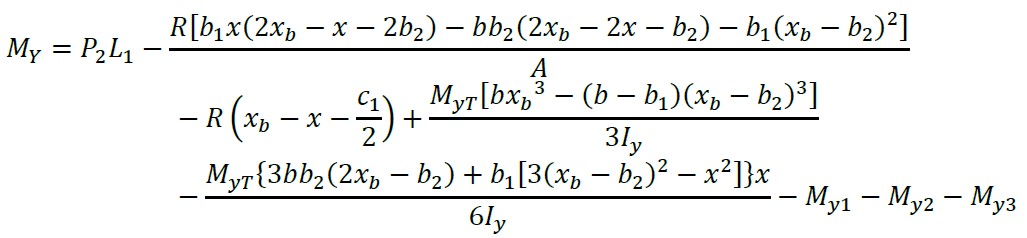
(36)

2.2 Cortantes por punção

As seções críticas para cortantes de punção são mostradas na Figura 5.

2.2.1 Cortantes por punção para o pilar de canto (pilar 1)

A seção crítica para o pilar 1 é apresentada no perímetro formado pelos pontos 1, 7, 8 e 9 da sapata (ver Figura 5). A cortante de punção é obtida pela carga axial do pilar 1 menos o volume de pressão da área delimitada pelos pontos 1, 7, 8 e 9:

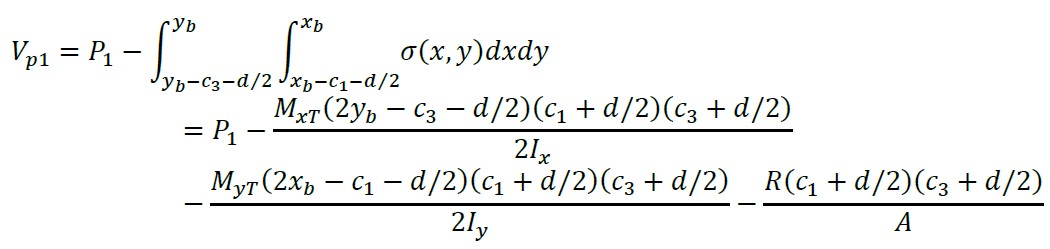
(37)

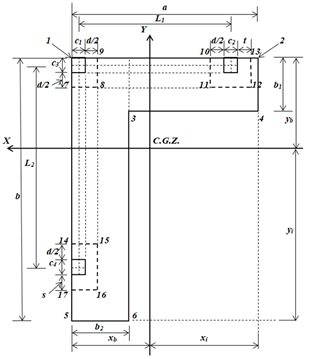
Figura 5. Seções críticas para cortante de punção

2.2.2 Cortantes por punção para o pilar límite (pilar 2)

A seção crítica para o pilar 2 é apresentada no perímetro formado pelos pontos 10, 11, 12 e 13 da sapata (ver Figura 5). A cortante de punção é obtida pela carga axial do pilar 2 menos o volume de pressão da área delimitada pelos pontos 10, 11, 12 e 13:

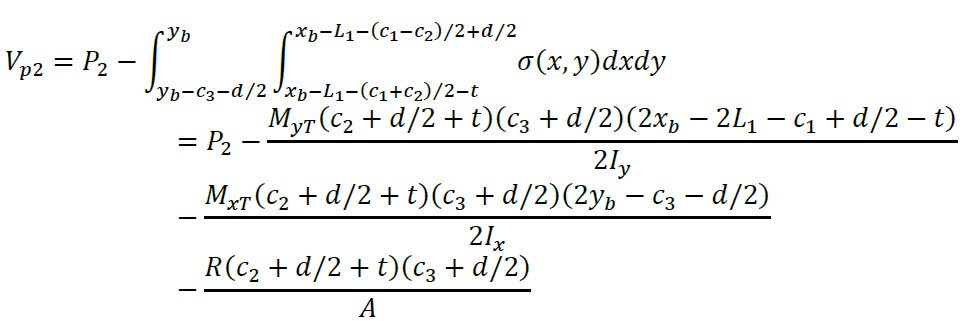
(38)

Nota: quando d/2 ≤ a - L₁ - (c₁ + c₂)/2 → t = d/2, e quando d/2 > a - L₁ - (c₁ + c₂)/2 → t = a - L₁ - (c₁ + c₂)/2.

2.2.3 Cortantes por punção para o pilar límite (pilar 3)

A seção crítica para o pilar 3 é apresentada no perímetro formado pelos pontos puntos 14, 15, 16 e 17 da sapata (ver Figura 5). A cortante de punção é obtida pela carga axial do pilar 3 menos o volume de pressão da área delimitada pelos pontos 14, 15, 16 e 17:

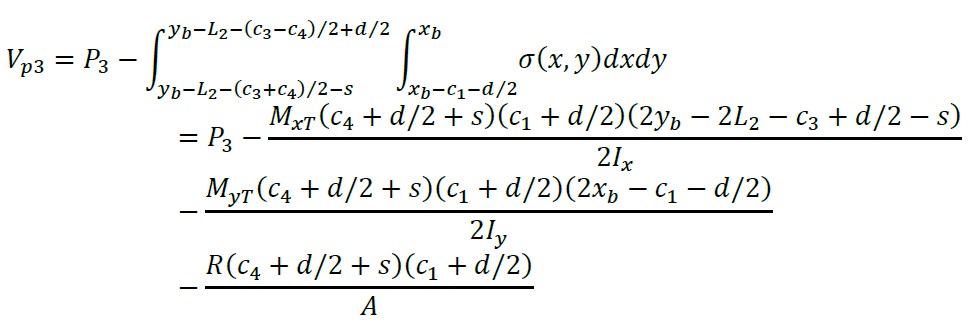
(39)

Nota: quando d/2 ≤ b - L₂ - (c₃ + c₄)/2 → s = d/2, e quando d/2 > b - L₂ - (c₃ + c₄)/2 → t = b - L₂ - (c₃ + c₄)/2.

3. Verificação do modelo proposto

O modelo proposto neste documento é verificado da seguinte forma:

1.- Para os momentos fletores nos eixos X₂ e X: Quando “y₂ = - b₁ / 2” é substituído na equação (7), M_X2 = 0 é obtido, se “y = y_b” é substituído na equação (11 ) obtemos M_X = 0 e, substituindo “y = y_b - b” na equação (26), obtemos M_X = 0. Portanto, as equações para os momentos fletores sobre os eixos X₂ e X obedecem ao equilíbrio.

2.- Para os momentos fletores nos eixos Y₃ e Y: Quando “x₃ = - b₂ / 2” é substituído na equação (28), M_Y3 = 0 é obtido, se “x = x_b” é substituído na equação (30 ) M_Y = 0 é obtido, e substituindo “x = x_b - a” na equação (36), M_Y = 0. Portanto, as equações para os momentos fletores nos eixos Y₃ e Y obedecem ao equilíbrio.

3.- Para cortantes de flexão nos eixos X₂ e X: Quando “y₂ = - b₁ / 2” é substituído na equação (4), V_y2 = 0 é obtido, se “y = y_b” é substituído na equação ( 8) obtemos V_y = 0, e substituindo “y = y_b - b” na equação (23) obtemos V_y = 0. Portanto, as equações para as cortantes de flexão nos eixos X₂ e X obedecem ao equilíbrio.

4.- Para os momentos fletores nos eixos Y₃ e Y: Quando “x₃ = - b₂ / 2” é substituído na equação (27), V_x3 = 0 é obtido, se “x = x_b” é substituído na equação (29 ) obtemos V_x = 0 e substituindo “x = x_b - a” na equação (35), obtemos V_x = 0. Portanto, as equações para as cortantes de flexão nos eixos Y₃ e Y estão de acordo com o equilíbrio.

4. Aplicação do modelo proposto

O projeto de uma combinação de sapata de canto que suporta três pilares quadrados é mostrado abaixo com as seguintes informações: Os três pilares são de 40x40 cm, L₁ = 5.00 m, L₂ = 5.00 m, H (profundidada da sapata) = 2.0 m, P_D1 = 300 kN, P_L1 = 200 kN, M_Dx1 = 80 kN-m, M_Lx1 = 70 kN-m, M_Dy1 = 120 kN-m, M_Ly1 = 80 kN-m, P_D2 = 600 kN, P_L2 = 400 kN, M_Dx2 = 160 kN-m, M_Lx2 = 140 kN-m, M_Dy2 = 120 kN-m, M_Ly2 = 80 kN-m, P_D3 = 500 kN, P_L3 = 400 kN, M_Dx3 = 120 kN-m, M_Lx3 = 80 kN-m, M_Dy3 = 150 kN-m, M_Ly3 = 100 kN-m, f’_c = 28 MPa, f_y = 420 MPa, q_a = 252 kN/m², γ_c (densidade do concreto) = 24 kN/m³, γ_s (densidade de preenchimento do solo) = 15 kN/m³.

As cargas e momentos atuando na sapata de canto combinada são: P₁ = 500 kN-m, M_x1 = 150 kN-m, M_y1 = 200 kN-m, P₂ = 1000 kN, M_x2 = 300 kN-m, M_y2 = 200 kN-m, P₃ = 900 kN, M_x3 = 200 kN-m, M_y3 = 250 kN-m.

A capacidade de suporte disponível do solo é considerada σ_máx = 213.00 kN/m², devido à capacidade de carga do solo “q_a” o próprio peso da sapata é subtraído (γ_c pela espessura da sapata), e o peso próprio do preenchimento do solo (γ_s pela espessura do preenchimento).

Sustituindo “σ_máx, L₁, L₂, P₁, M_x1, M_y1, P₂, M_x2, M_y2, P₃, M_x3, M_y3” nas equações (30) a (42) do trabalho (López-Chavarría et al. 2017), e a solução por software MAPLE-15 se obtém: A_min = 11.31 m², M_xT = − 8.65 kN-m, M_yT = 9.49 kN-m, R = 2400 kN, a = 6.36 m, b = 5.95 m, b₁ = 1.00 m, b₂ = 1.00 m, σ₁ = 211.31 kN/m², σ₂ = 212.75 kN/m², σ₃ = 211.78 kN/m², σ₄ = 213.00 kN/m², σ₅ = 212.77 kN/m², σ₆ = 213.00 kN/m².

As dimensões práticas da sapata combinada de canto que suporta três pilares quadrados são: a = 6.40 m, b = 6.00 m, b₁ = 1.00 m, b₂ = 1.00 m. Agora, as dimensões práticas para verificar as tensões são substituídas no mesmo software MAPLE-15, e a solução é: A_min = 11.40 m², M_xT = 27.89 kN-m, M_yT = 7.89 kN-m, R = 2400 kN, a = 6.40 m, b = 6.00 m, b₁ = 1.00 m, b₂ = 1.00 m, σ₁ = 212.30 kN/m², σ₂ = 211.11 kN/m², σ₃ = 211.34 kN/m², σ₄ = 210.34 kN/m², σ₅ = 207.68 kN/m², σ₆ = 207.49 kN/m².

As propriedades geométricas da sapata são: x_b = 2.02 m, y_b = 1.82 m, I_x = 36.21 m⁴, I_y = 42.73 m⁴.

As cargas fatoradas e os momentos que atuam na sapata são: P_u1 = 680 kN, M_ux1 = 208 kN-m, M_uy1 = 272 kN-m, P_u2 = 1360 kN, M_ux2 = 416 kN-m, M_uy2 = 272 kN-m, P_u3 = 1240 kN, M_ux3 = 272 kN-m, M_uy3 = 340 kN-m. As cargas e momentos resultantes fatorados pelas equações (31) a (33) (López-Chavarría et al., 2017) são obtidas: R_u = 3280 kN, M_uxT = − 4.21 kN-m, M_uyT = 39.79 kN-m.

O momento sobre o eixo a'-a' pela equação (7) é obtido “M_a’ = 289.15 kN-m” em y₂ = b₁/2 - c₃. O momento sobre o eixo b’-b’ pela equação (16) ) é obtido “M_b’ = − 1335.85 kN-m” em y = y_b - b₁. Agora, substituindo os valores correspondentes na equação (21) e diferenciando com relação a “y”, isso é igual a zero para obter a localização do momento máximo “y_m = 0.12 m”, posteriormente se substitui na equação (21), e o momento é “M_c’ = − 1405.08 kN-m”. O momento sobre o eixo d’-d’ pela equação (21) é obtido “M_d’ = 168.08 kN-m” em y = y_b - L₂ - c₃/2 + c₄/2. O momento sobre o eixo e’-e’ pela equação (26) é obtido “M_e’ = 51.87 kN-m” em y = y_b - L₂ - c₃/2 - c₄/2.

O momento sobre o eixo f’-f’ pela equação (28) ) é obtido “M_f’ = 238.18 kN-m” em x₃ = b₂/2 - c₁. O momento sobre o eixo g’-g’ pela equação (32) é obtido “M_g’ = − 1280.14 kN-m” em x = x_b - b₂. Agora, substituindo os valores correspondentes na equação (34) e diferenciando com relação a “x”, isso é igual a zero para obter a localização do momento máximo “x_m = 0.37 m”, posteriormente se substitui na equação (34), e o momento é “M_h’ = − 1339.60 kN-m”. O momento sobre o eixo i’-i’ pela equação (34) é obtido “M_i’ = 278.39 kN-m” em x = x_b - L₁ - c₁/2 + c₂/2. O momento sobre o eixo j’-j’ pela equação (36) é obtido “M_j’ = 141.97 kN-m” em x = x_b - L₁ - c₁/2 - c₂/2.

A escala efetiva no pilar 2 é: 18.33 cm. A escala efetiva para o momento máximo “M_c’” é: 46.42 cm. A escala efetiva no pilar 3 é: 16.63 cm. A escala efetiva para o momento máximo “M_h’” é 45.32 cm. A escala efetiva depois de fazer várias propostas é: d = 92.00 cm, r = 8.00 cm e t = 100 cm.

A Tabela 1 mostra as cortantes de flexão que atuam na sapata e aquelas resistidas pelo concreto de acordo com a norma (ACI 318S-14).

Tabela 1. Cortantes por flexão.

Eixos Coordenadas Largura de análise cm Cortantes por flexão

Atuantes kN Resistidos kN

k' y₂ = b₁/2 – c₃ – d 132 0* 928.56

l' y = y_b – c₃ – d 100 114.14 703.45

m' y = y_b – c₃/2 – L₂ + c₄/2 + d 100 – 684.15 703.45

n' y = y_b – c₃/2 – L₂ – c₄/2 – d 100 0* 703.45

o' x₃ = b₂/2 – c₁ – d 132 0* 928.56

p' x = x_b – c₁ – d 100 92.11 703.45

q' x = x_b – c₁/2 – L₁ + c₂/2 + d 100 – 699.81 703.45

r' y = y_b – c₃/2 – L2 – c₄/2 – d 100 22.68 703.45

* O eixo está localizado fora da área da sapata.

Tabela 1. Cortantes por flexão.
Eixos	Coordenadas	Largura de análise cm	Cortantes por flexão
Atuantes kN	Resistidos kN
k'	y₂ = b₁/2 – c₃ – d	132	0*	928.56
l'	y = y_b – c₃ – d	100	114.14	703.45
m'	y = y_b – c₃/2 – L₂ + c₄/2 + d	100	– 684.15	703.45
n'	y = y_b – c₃/2 – L₂ – c₄/2 – d	100	0*	703.45
o'	x₃ = b₂/2 – c₁ – d	132	0*	928.56
p'	x = x_b – c₁ – d	100	92.11	703.45
q'	x = x_b – c₁/2 – L₁ + c₂/2 + d	100	– 699.81	703.45
r'	y = y_b – c₃/2 – L2 – c₄/2 – d	100	22.68	703.45
* O eixo está localizado fora da área da sapata.

A Tabela 2 mostra as cortantes de punção atuando na sapata e resistidas pelo concreto de acordo com a norma (ACI 318S-14).

Tabela 2. Cortantes por punção.

Pilar Perímetro crítico Cortantes por punção

Atuantes kN Resistidos kN

1 b₀ = c₁ + c₃ + d 466.23 3629.81 7500.95 2348.70

2 b₀ = c₂ + 2c₃ + 2d 1036.93 6415.49 13112.93 4151.20

3 b₀ = 2c₁ + c₄ + 2d 911.26 6415.49 13112.93 4151.20

Tabela 2. Cortantes por punção.
Pilar	Perímetro crítico	Cortantes por punção
Atuantes kN	Resistidos kN
1	b₀ = c₁ + c₃ + d	466.23	3629.81	7500.95	2348.70
2	b₀ = c₂ + 2c₃ + 2d	1036.93	6415.49	13112.93	4151.20
3	b₀ = 2c₁ + c₄ + 2d	911.26	6415.49	13112.93	4151.20

A Tabela 3 mostra o aço de armadura para a sapata combinada de canto (ACI 318S-14).

Tabela 3. Aço da armadura da sapata.

Aço da armadura Área cm2

Direção do eixo "Y" Armadura na parte superior com largura b₂ Armadura principal 42.10

Armadura mínima 30.67

Armadura proposta 45.63 (9Ø1")

Armadura na parte superior com largura a − b₂ Armadura por temperatura 97.20

Armadura proposta 99.75 (35Ø3/4")

Armadura na parte inferior com largura b₂ Armadura principal 4.86

Armadura mínima 30.67

Armadura proposta 35.49 (7Ø1")

Armadura debajo de la columna 2 com largura w₂ Armadura principal 8.37

Armadura mínima 40.48

Armadura proposta 42.75 (15Ø3/4")

Armadura na parte inferior com largura a − b₂ − w₂ Armadura por temperatura 73.44

Armadura proposta 74.10 (26Ø3/4")

Direção do eixo "X" Armadura na parte superior com largura b₁ Armadura principal 40.06

Armadura mínima 30.67

Armadura proposta 40.56 (8Ø1")

Armadura na parte superior com largura b – b₁ Armadura por temperatura 90.00

Armadura proposta 91.20 (32Ø3/4")

Armadura na parte inferior com largura b₁ Armadura principal 8.07

Armadura mínima 30.67

Armadura proposta 35.49 (7Ø1")

Armadura debajo de la columna 3 com largura w₃ Armadura principal 6.88

Armadura mínima 40.48

Armadura proposta 42.75 (15Ø3/4")

Armadura na parte inferior com largura b – b₁ – w₃ Armadura por temperatura 66.24

Armadura proposta 68.40 (24Ø3/4")

Tabela 3. Aço da armadura da sapata.
Aço da armadura	Área cm2
Direção do eixo "Y"	Armadura na parte superior com largura b₂	Armadura principal	42.10
Armadura mínima	30.67
Armadura proposta	45.63 (9Ø1")
Armadura na parte superior com largura a − b₂	Armadura por temperatura	97.20
Armadura proposta	99.75 (35Ø3/4")
Armadura na parte inferior com largura b₂	Armadura principal	4.86
Armadura mínima	30.67
Armadura proposta	35.49 (7Ø1")
Armadura debajo de la columna 2 com largura w₂	Armadura principal	8.37
Armadura mínima	40.48
Armadura proposta	42.75 (15Ø3/4")
Armadura na parte inferior com largura a − b₂ − w₂	Armadura por temperatura	73.44
Armadura proposta	74.10 (26Ø3/4")
Direção do eixo "X"	Armadura na parte superior com largura b₁	Armadura principal	40.06
Armadura mínima	30.67
Armadura proposta	40.56 (8Ø1")
Armadura na parte superior com largura b – b₁	Armadura por temperatura	90.00
Armadura proposta	91.20 (32Ø3/4")
Armadura na parte inferior com largura b₁	Armadura principal	8.07
Armadura mínima	30.67
Armadura proposta	35.49 (7Ø1")
Armadura debajo de la columna 3 com largura w₃	Armadura principal	6.88
Armadura mínima	40.48
Armadura proposta	42.75 (15Ø3/4")
Armadura na parte inferior com largura b – b₁ – w₃	Armadura por temperatura	66.24
Armadura proposta	68.40 (24Ø3/4")

Os efeitos que governam a espessura da sapata são os momentos de flexão, as cortantes de flexão e as cortantes de punção, e o aço da armadura é projetado por momentos. Para a espessura do exemplo numérico, o cisalhamento de flexão no eixo q'-q ' governa (consulte a Tabela 1).

A Tabela 4 mostra o comprimento mínimo de desenvolvimento para barras deformadas "l_d" e o comprimento disponível "l_a". Portanto, o comprimento disponível é maior do que o comprimento mínimo de desenvolvimento em ambas as direções (superior e inferior) (consulte a Tabela 4). Portanto, não são necessários ganchos para a sapata combinada de canto.

Tabela 4. Comprimento mínimo de desenvolvimento e comprimento disponível.

Localização da armadura ψt ψe = λ Comprimento de desenvolvimento cm Comprimento disponível

Direção do eixo "X" cm Direção do eixo "Y" cm

Parte superior 1.3 1.0 154.17 165 170

Parte inferior 1.0 1.0 96.00 140 100

Tabela 4. Comprimento mínimo de desenvolvimento e comprimento disponível.
Localização da armadura	ψt	ψe = λ	Comprimento de desenvolvimento cm	Comprimento disponível
Direção do eixo "X" cm	Direção do eixo "Y" cm
Parte superior	1.3	1.0	154.17	165	170
Parte inferior	1.0	1.0	96.00	140	100

A Figura 6 mostra o aço da armadura e as dimensões da sapata de canto combinada em detalhes.

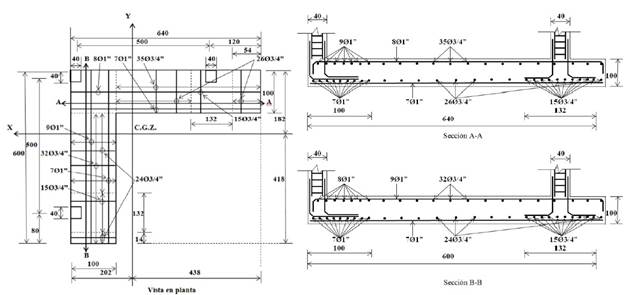
Figura 6. Projeto final da sapata combinada de canto

5. ConclusÕes

O novo modelo apresentado neste trabalho é aplicado apenas para o projeto de sapatas de canto combinadas. As considerações deste trabalho são: o membro estrutural é rígido e o solo que sustenta a sapata é elástico e homogêneo, o que obedece à equação de flexão biaxial, ou seja, a pressão varia linearmente.

O novo modelo apresentado neste documento conclui o seguinte:

1.- A espessura das sapatas angulares combinadas é determinada pela resistência à flexão e as sapatas isoladas são determinadas pela resistência à punção.

2.- O novo modelo não é limitado, enquanto o projeto atual considera que a pressão máxima em todos os pontos de contato, ou seja, a força resultante das cargas aplicadas coincide com a posição do centro geométrico da sapata.

3.- O novo modelo está mais ajustado às condições reais em relação ao desenho atual, pois o novo modelo leva em consideração a pressão linear do terreno e o desenho atual considera a pressão uniforme sobre toda a superfície de contato e esta é a pressão máxima.

4.- O novo modelo para o dimensionamento de sapatas de canto combinadas sujeitas a carregamento axial e dois momentos em direções ortogonais devido a cada pilar considera duas linhas de propriedade restritas, mas pode ser aplicado a três linhas de propriedade.

O novo modelo mostrado neste trabalho em termos de cargas aplicadas em cada pilar pode ser aplicado a: 1) Carga sem momentos, 2) Carga e um momento (flexão uniaxial), 3) Carga e dois momentos ortogonais (flexão biaxial).

Portanto, o modelo proposto é o mais adequado, pois gera um melhor controle de qualidade dos recursos utilizados.

As seguintes investigações podem ainda ser implementadas: 1) Uma continuação deste trabalho seria formular o custo mínimo para as sapatas de canto combinadas; 2) Quando as sapatas de canto combinadas suportam mais de dois pilares em cada direção; 3) O modelo proposto pode ser estendido para o projeto de lajes de fundação; 4) Quando a sapata é movida sobre outro tipo de solo, por exemplo em solos totalmente argilosos (solos coesos) ou em solos totalmente arenosos (solos granulares), o diagrama de pressão é diferente do linear e o diagrama pode ser parabólico (ver Figura 1).

REFERÊNCIAS

Abdrabbo, F., Mahmoud, Z. I. and Ebrahim, M. (2016), Structural design of isolated column footings. Alexandria Engineering Journal. 55(3):2665-2678. https://doi.org/10.1016/j.aej.2016.06.016

ACI 318S-14 (2014), “Building Code Requirements for Structural Concrete and Commentary, Committee 318”, New York, USA.

Anil, Ö, Akbaş, S.O., BabagĪray, S., Gel, A.C. and Durucan, C. (2017), Experimental and finite element analyses of footings of varying shapes on sand. Geomechanics and Engineering. 12(2):223-238. https://doi.org/10.12989/gae.2017.12.2.223

Aydogdu, I. (2016), New Iterative method to Calculate Base Stress of Footings under Biaxial Bending. International Journal of Engineering & Applied Sciences (IJEAS). 8(4):40-48. https://doi.org/10.24107/ijeas.281460

Balachandar, S. and Narendra Prasad, D. (2017), Analysis and Design of Various Types of Isolated Footings. International Journal of Innovative Research in Science, Engineering and Technology. 6(3):3980-3986. http://www.ijirset.com/upload/2017/march/173_balachandar%20pmu.pdf

Bowles, J. E. (2001), “Foundation analysis and design”. McGraw-Hill, New York, USA.

Chen, W-R., Chen, C-S and Yu, S-Y. (2011), Nonlinear vibration of hybrid composite plates on elastic foundations. Structural Engineering & Mechanics. 37(4):367-383. https://doi.org/10.12989/sem.2011.37.4.367

Das, B.M., Sordo-Zabay, E., Arrioja-Juarez, R. (2006), “Principios de ingeniería de cimentaciones”, Cengage Learning Latín América, Distrito Federal, México.

Dezhkam, B. and Yaghfoori, A. (2018), Soil foundation effect on the vibration response of concrete foundations using mathematical model. Computers and Concrete. 22(2):221-225. https://doi.org/10.12989/cac.2018.22.2.221

El-kady, M. S. and Badrawi, E. F. (2017), Performance of isolated and folded footings. Journal of Computational Design and Engineering. 4:150-157. https://doi.org/10.1016/j.jcde.2016.09.001

Sawwaf, M. and Nazir, A. K. (2010), Behavior of repeatedly loaded rectangular footings resting on reinforced sand. Alexandria Engineering Journal. 49:349-356. https://doi.org/10.1016/j.aej.2010.07.002

Fillo, L., Augustin, T. and Knapcová, V. (2016), Influence of footings stiffness on punching resistance. Perspectives in Science. 7:204-207. https://doi.org/10.1016/j.pisc.2015.11.034

Ibrahim, A., Dif, A. and Othman, W. (2018), Nonlinearity analysis in studying shallow grid foundation. Alexandria Engineering Journal. 57:859-866. https://doi.org/10.1016/j.aej.2016.11.021

Khajehzadeh, M., Taha, M. R., El-Shafie, A. and Eslami, M. (2011), Modified particle swarm optimization for optimum design of spread footing and retaining wall. Journal of Zhejiang University-SCIENCE A. 12(6):415-427. https://link.springer.com/article/10.1631/jzus.A1000252

Kurian, N. P. (2005), “Design of foundation systems”, Alpha Science Int'l Ltd., New Delhi, India.

López-Chavarría, S., Luévanos Rojas, A. and Medina Elizondo, M. (2017), Optimal dimensioning for the corner combined footings. Advances in Computational Design. 2(2):169-183. https://doi.org/10.12989/acd.2017.2.2.169

Luévanos-Rojas, A., Faudoa-Herrera, J. G., Andrade-Vallejo, R. A. and Cano-Alvarez, M. A. (2013), Design of Isolated Footings of Rectangular Form Using a New Model. International Journal of Innovative Computing, Information and Control. 9(10):4001-4022. http://www.ijicic.org/ijicic-12-10031.pdf

Luévanos-Rojas, A. (2014a), Design of isolated footings of circular form using a new model. Structural Engineering and Mechanics. 52(4):767-786. https://doi.org/10.12989/sem.2014.52.4.767

Luévanos-Rojas, A. (2014b), Design of boundary combined footings of rectangular shape using a new model. Dyna-Colombia. 81(188):199-208. http://dx.doi.org/10.15446/dyna.v81n188.41800

Luévanos-Rojas, A. (2015), Design of boundary combined footings of trapezoidal form using a new model. Structural Engineering and Mechanics. 56(5):745-765. https://doi.org/10.12989/sem.2015.56.5.745

Luévanos-Rojas, A. (2016a), A comparative study for the design of rectangular and circular isolated footings using new models. Dyna-Colombia. 83(196):149-158. http://dx.doi.org/10.15446/dyna.v83n196.51056

Luévanos-Rojas, A. (2016b), A new model for the design of rectangular combined boundary footings with two restricted opposite sides. Revista ALCONPAT. 6(2):172-187. https://doi.org/10.21041/ra.v6i2.137

Luévanos-Rojas, A., López-Chavarría, S. and Medina-Elizondo, M. (2017a), Optimal design for rectangular isolated footings using the real soil pressure. Ingeniería e Investigación. 37(2):25-33. http://dx.doi.org/10.15446/ing.investig.v37n2.61447

Luévanos-Rojas, A., Barquero-Cabrero, J. D., López-Chavarría, S. and Medina-Elizondo, M. (2017b), A comparative study for design of boundary combined footings of trapezoidal and rectangular forms using new models. Coupled Systems Mechanics. 6(4):417-437. https://doi.org/10.12989/csm.2017.6.4.417

Luévanos-Rojas, A., López-Chavarría, S. & Medina-Elizondo, M. (2018), A new model for T-shaped combined footings Part II: Mathematical model for design. Geomechanics and Engineering. 14(1):61-69. https://doi.org/10.12989/gae.2018.14.1.061

Magade, S. B. and Ingle, R. K. (2019), Numerical method for analysis and design of isolated square footing under concentric loading. International Journal of Advanced Structural Engineering. 11:9-20. https://doi.org/10.1007/s40091-018-0211-3

Punmia, B. C., Kumar-Jain, A., Kumar-Jain, A. (2007), “Limit state design of reinforced concrete”, Laxmi Publications (P) Limited, New Delhi, India.

Santos, D. F. A., Lima Neto, A. F. and Ferreira, M. P. (2018), Punching shear resistance of reinforced concrete footings: evaluation of design codes. IBRACON Structures and Materials Journal. 11(2):432-454. https://doi.org/10.1590/s1983-41952018000200011

Shahin M. A. and Cheung E. M. (2011), Stochastic design charts for bearing capacity of strip footings. Geomechanics and Engineering. 3(2):153-167. http://hdl.handle.net/20.500.11937/6498

Tahmasebi poor, A., Barari, M., Behnia, M. and Najafi, T. (2015), Determination of the ultimate limit states of shallow foundations using gene expression programming (GEP) approach. Soils and Foundations. 55(3):650-659. https://doi.org/10.1016/j.sandf.2015.04.015

Varghese, P. C. (2009), “Design of reinforced concrete foundations”, PHI Learning Pvt. Ltd., New Delhi, India.

Yáñez-Palafox, J.A., Luévanos-Rojas, A., López-Chavarría, S. and Medina-Elizondo, M. (2019), Modeling for the strap combined footings Part II: Mathematical model for design. Steel and Composite Structures. 30(2):109-121. https://doi.org/10.12989/scs.2019.30.2.109