Investigación Básica

Desarrollo y análisis de un modelo numérico de expansión de concreto reforzado sujeto a corrosión uniforme

Development and analysis of a numerical model of the reinforced concrete expansion due to uniform corrosion

Desenvolvimento e análise de um modelo numérico da expansão do concreto armado sujeito à corrosão uniforme

E. F. Felix¹ ^* , R. Carrazedo¹ , E. Possan² , E. S. Ramos¹

¹ University of São Paulo at São Carlos School of Engineering, Brasil.

² Universidade Federal da Integração Latino-Americana (UNILA), Brasil.

^*Autor de Contacto: emerson.felipe.felix@gmail.com

Recepción: 21 de febrero de 2019.
Aceptación: 11 de diciembre de 2019.
Publicación: 01 de septiembre de 2020

Citar como: Felix, E. F., Carrazedo, R., Possan, E., Ramos, E. S. (2020), "Desarrollo y análisis de un modelo numérico de expansión de concreto reforzado sujeto a corrosión uniforme", Revista ALCONPAT, 10 (3), pp. 300–316, DOI: https://doi.org/10.21041/ra.v10i3.395.

Resumen
Este trabajo presenta la modelización y análisis de los efectos de la corrosión por carbonatación en elementos de concreto reforzado a través de un modelo numérico basado en el Método de los Elementos Finitos. Para controlar y minimizar el daño asociado a la corrosión se hace necesario disponer de herramientas y conocimientos suficientes para comprender los efectos de esta manifestación patológica sobre el comportamiento mecánico del concreto reforzado. Ante los resultados obtenidos, se constató que, dependiendo del nivel de corrosión de las armaduras, el elemento de concreto tiene su estado de tensión y deformación alterado. Además, los resultados indican la eficiencia del modelo desarrollado y su aplicabilidad frente a la simulación del comportamiento mecánico del concreto reforzado con corrosión uniforme.
Palabras clave: concreto reforzado, corrosión, modelización numérica, método de los elementos finitos.

Abstract
This paper presents the modeling and analysis of the corrosion effects due to carbonation on reinforced concrete elements through a numerical model based on the Finite Element Method. In order to minimize corrosion damage, tools are required to understand the pathological manifestation on the mechanical behavior of reinforced concrete. It was found that depending on the reinforcement corrosion stage, the state of stress and deformation of the concrete element is compromised. Besides, results show the efficiency of the developed model and its applicability to the simulation of the mechanical behavior of reinforced concrete structures subjected to uniform corrosion.
Keywords: reinforced concrete, corrosion, numerical modeling, finite element method.

Resumo
Este trabalho apresenta a modelagem e análise dos efeitos da corrosão por carbonatação em elementos de concreto armado através de um modelo numérico baseado no Método dos Elementos Finitos. Para controlar e minimizar os danos associados à corrosão faz-se necessário deter ferramentas e conhecimento suficientes para entender os efeitos desta manifestação patológica sobre o comportamento mecânico do concreto armado. Diante dos resultados obtidos, constatou-se que a depender do nível de corrosão das armaduras, o elemento de concreto tem seu estado de tensão e deformação comprometido. Ademais, os resultados apontam a eficiência do modelo desenvolvido e a sua aplicabilidade frente à simulação do comportamento mecânico de estruturas de concreto armado sujeitas à corrosão uniforme.
Palavras-chave: concreto armado, corrosão, modelagem numérica, método dos elementos finitos.

1. Introducción

La degradación de estructuras de concreto reforzado debido a la acción de la corrosión de las armaduras es de difícil medición por la complejidad del fenómeno físico-químico y de los múltiples parámetros ahí involucrados (Mehta y Monteiro, 2014). Del punto de vista de la mecánica de materiales y de las estructuras, el principal efecto de la corrosión para las armaduras consiste en la pérdida de masa del acero y, por consecuencia, en la transformación de este material en los productos de corrosión, o herrumbre, como se les conocen comúnmente. Los productos de la corrosión poseen naturaleza expansiva, generando tensiones en el interior del concreto que llevan a su fisuración y desprendimiento a lo largo del tiempo.

En general, el concreto presenta condiciones suficientes para la protección de las armaduras contra la corrosión, gracias a la alta alcalinidad de la pasta (pH entre 12 y 13). Sin embargo, esa protección se pierde a medida que el concreto es sujeto a diferentes agentes agresivos presentes en la atmósfera, por ejemplo, iones cloruro (Cl^-) y dióxido de carbono (CO₂) (Gentil, 2011).

Dependiendo de la concentración del agente agresivo presente en la atmósfera, el proceso corrosivo puede ser clasificado como uniforme o localizado. La corrosión localizada o por picadura ocurre cuando iones cloruro causan un aumento de la conductividad eléctrica del concreto y atacan la capa pasiva que protege las armaduras. En este tipo de corrosión solo algunas regiones de la armadura pierden masa de acero, justificando el término “localizada”, usado para su clasificación (Ribeiro et al., 2015).

El proceso corrosivo es dicho uniforme o por carbonatación cuando el contenido de CO₂ presente en la atmósfera es preponderante al de iones cloruro. En este caso, la difusión de CO₂ en el concreto resulta en la disminución del pH de la matriz cementícia (de aproximadamente 13 o 12 hasta 9), lo que lleva a destrucción de la capa pasiva que recubre las armaduras, tornando el acero susceptible a la corrosión (Mehta e Monteiro, 2014).

La corrosión uniforme ocurre predominantemente en estructuras con concreto de baja calidad, en lugares donde el recubrimiento de la armadura es insuficiente para garantizar la protección del acero o en ambientes de severa agresividad (Ribeiro et al., 2015). Helene (1986) ha verificado que, en esos casos, la corrosión lleva a la formación de productos de corrosión en la interfaz entre el acero y el concreto, y que eses pueden ocupar un espacio 3 a 10 veces mayor a lo inicial.

De acuerdo a Andrade et al. (1993) y Ribeiro et al. (2015), la formación y desarrollo de los productos de corrosión debido a la corrosión uniforme dependen de diversos factores, sean estos ambientales (temperatura del ambiente, humedad relativa del aire, grado de agresividad del ambiente, exposición al CO₂, entre otros) o constructivos (tipo de cemento usado en la producción del concreto, relación agua/cemento del concreto, tipo de acero, dimensiones del recubrimiento de las armaduras, entre otros).

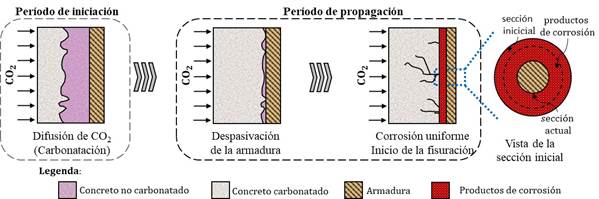
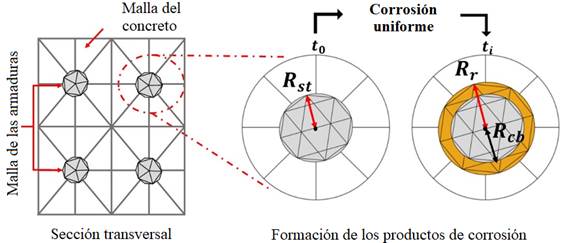
Con la formación de los productos de corrosión, campos internos de tensión son generados en la interfaz del acero con el concreto. A medida que las tensiones generadas por los productos de corrosión se vuelven superiores a las resistidas por el concreto, microfisuras se manifiestan en la matriz del concreto que, con la progresión de las manifestaciones patológicas, aumentan de tamaño y espesor, propagándose por todo el elemento estructural hasta causar el desprendimiento del concreto de recubrimiento, afectando la durabilidad y reduciendo la vida útil de la estructura. El proceso de degradación se muestra en la Figura 1.


Figura 1. Evolución de la corrosión en el concreto.

A fin de minimizar los efectos de la corrosión es necesario conocer las formas de iniciación y propagación del proceso corrosivo, lo que posibilita la reducción de su incidencia y, en casos avanzados, la reparación y/o restauración de las estructuras a manera de aumentar su vida útil y reducir riesgos y daños a sus usuarios.

Para el estudio de la corrosión y de sus efectos en el comportamiento mecánico del concreto reforzado, se llevaron a cabo algunos trabajos experimentales (Molina et al., 1993; Almusallam, 2001; Graeff, 2007; Zhu, 2014), los cuales resultaran en descubrimientos relevantes para el área. Sin embargo, tres importantes limitaciones son apuntadas por los investigadores: (i) la dificultad de estudiar aisladamente los diferentes factores que influencian en el proceso de corrosión; (ii) elevados costos y (iii) tiempo necesario para la realización de los experimentos.

Con el avance de la computación, diversas herramientas numéricas fueran desarrolladas, por ejemplo, el método de los elementos de contorno (MEC), el método de los elementos finitos (MEF), redes neurales artificiales (RNA), entre otras, haciendo que los investigadores del área las usen para la creación de modelos numéricos, una vez que esas herramientas se presentan como una alternativa eficiente para la superación de los limites anteriormente mencionados.

Teniendo eso en cuenta, Hansen y Saouma (1999), Maruya et al. (2003) y Bhargava et al. (2005) usaron diferentes herramientas numéricas para la resolución de forma automatizada de ecuaciones matemáticas referentes a los mecanismos de corrosión, lo que posibilito el análisis de los efectos de corrosión y su propagación. Procedimientos semejantes fueron adoptados por Isgor y Razaqpur (2006), Xu et al. (2009), Du y Jin (2014), Ožbolt et al. (2014) y Paul y Zijl (2016), pero los autores solucionaron el problema químico-mecánico, relativo a la corrosión en elementos de concreto reforzado, vía método de los elementos finitos.

De esta manera, se dio continuidad al uso de herramientas numéricas para el estudio de la corrosión y sus efectos y en el presente trabajo un modelo numérico desarrollado vía método de los elementos finitos posicional (MEFP) es presentado y analizado. El modelo desarrollado posibilita la simulación de la expansión del concreto reforzado debido a la corrosión uniforme y, en especial, a la formación de los productos de corrosión.

2. Modelo de expansión del concreto debido a la corrosión

2.1 Modelo mecánico

Con el objetivo de simular la expansión del concreto reforzado debido a la corrosión uniforme, en especial a la formación de los productos de corrosión, se desarrolló una herramienta numérica basada en el método de los elementos finitos posicional (MEFP). El código se llevó a cabo en lenguaje Fortran y considera diferentes formulaciones analíticas para la determinación de parámetros representativos de corrosión.

Para la determinación del comportamiento mecánico del concreto reforzado, se empleó una formulación basada en el MEFP para sólidos compuestos, desarrollada en Vanalli et al. (2008) y Paccola y Coda (2016), donde los parámetros nodales que se consideran son las posiciones y las deformaciones que se miden con relación a la posición inicial del cuerpo. La medida de deformación es la de Green y la ley constitutiva de los materiales es de Saint-Venant-Kirchhoff.


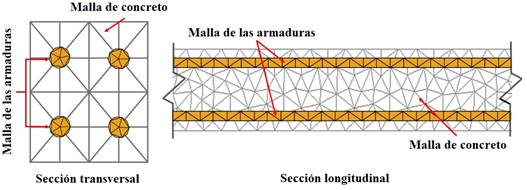
Figura 2. Discretización de la sección transversal y longitudinal de una viga de concreto.

El concreto reforzado es discretizado teniendo en cuenta la matriz de concreto y armaduras (Figura 2). Tanto la matriz de concreto como las armaduras son representadas por medio de elementos finitos bidimensionales triangulares planos, siendo la malla de armaduras acoplada a de la matriz de concreto por medio de la técnica de la embutición, descrita en Vanalli et al. (2008) y Paccola y Coda (2016). En este caso ocurre una adherencia perfecta entre la partícula y la matriz, haciendo que el uso de elementos de partículas no aumente los grados de libertad del sistema. Todos los grados de libertad de los elementos de partículas son escritos en función de los elementos de la matriz.

En la secuencia se presenta de manera sucinta el proceso empleado en este trabajo para obtención de la respuesta mecánica de un problema vía MEFP para el concreto reforzado.

Considerando fuerzas conservativas y el principio de la mínima energía potencial estacionaria para la solución del problema no lineal geométrico, la energía potencial total de un sólido compuesto particulado es descrita en (1).

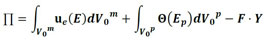(1)

en la que Θ es la energía específica de deformación de las partículas, u_e es la energía específica de deformación de la matriz, F es el vector de fuerzas conservativas externas, Y es el vector de posición nodal, E_p es la deformación desarrollada en las partículas, calculada conforme sigue en (2), E es la deformación desarrollada en la matriz, también calculada conforme (2), y V₀^p y V₀^m representan los volúmenes iniciales de las partículas y de la matriz, respectivamente.

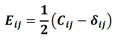(2)

en la que E_ij representa la parte elástica de deformación, C_ij es el tensor de estiramiento a la derecha de Cauchy-Green y δ_ij representa la delta de Kronecker.

Considerando que la variación de energía potencial total es igual a cero en la configuración de equilibrio, el problema consiste en encontrar el vector de posición nodal que remite a esa posición, conforme se presenta en (3).

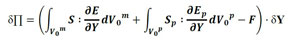(3)

en la que S es el segundo tensor de tensiones de Piola-Kirchhoff desarrollado en la matriz elástica y S_p es el segundo tensor de tensiones de Piola-Kirchhoff desarrollado en las partículas.

La solución de (3) se logra por medio del proceso iterativo de Newton-Raphson, lo cual utiliza como estrategia de solución un vector de desequilibrio de fuerzas g , conforme sigue en (4).

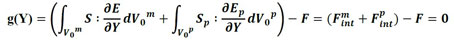(4)

en la que F^m_int es el vector de fuerzas internas de la matriz y F^p_int es el vector de fuerzas internas de las partículas. La ecuación (4) involucra un proceso no lineal por lo que es expandida por serie de Taylor, conforme se detalla en (5).

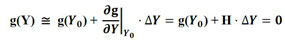(5)

en la que Y es una posición tentativa y H es la matriz Hessiana (o matriz de rigidez tangente).

Las fuerzas son conservativas, H puede ser descompuesta en dos matrices, una referente a contribución de rigidez de los elementos de la matriz (H_m) y otra de los elementos de partículas (H_p), como se describe en (6).

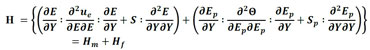(6)

La solución del sistema no lineal presentada en (5) por el método de Newton-Raphson fornece la corrección de la posición (Y = Y₀ + ∆Y) y el procedimiento es repetido hasta que |∆Y|/|X| sea menor a una determinada tolerancia, siendo X el vector de las posiciones nodales de configuración inicial.

Mayores detalles acerca de las deducciones de las ecuaciones aquí descritas y del proceso de acoplamiento de los elementos de partícula a la matriz pueden ser vistos en Paccola y Coda (2016) y Coda (2018).

2.2 Modelo de corrosión

Compreder como se desarrollan y se distribuyen los productos de corrosión alrededor de la sección de la armadura posibilita la determinación de modelos y herramientas que son capaces de describir los campos de deformación y de tensión que surgen en las estructuras de concreto reforzado sujetas a la corrosión. Estos modelos ayudan en los estudios referentes a los efectos de la corrosión involucrados con el comportamiento mecánico del concreto, la durabilidad y la vida útil de las armaduras.

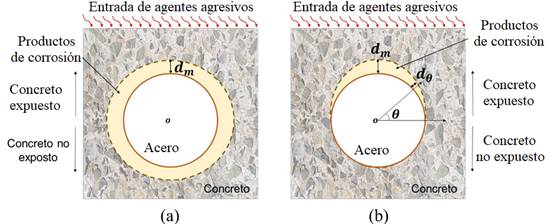
A lo largo de los últimos años, algunos modelos fueron propuestos con objetivo de representar y describir el perfil de distribución de los productos de corrosión en el entorno de las armaduras, como ejemplo Liu y Weyers (1998), Yuan y Ji (2009), Balafas y Burgoyne (2010) y Kiani y Shodja (2011). En cuanto al perfil de formación y distribución de los productos de corrosión, ellos están divididos en lineal y no lineal, conforme se presenta en la Figura 3.


Figura 3. Perfil de formación de los productos de corrosión: (a) lineal y (b) no lineal.

Por tanto, considerando que la corrosión desencadenada por la carbonatación del concreto de recubrimiento se desarrolla en toda la armadura, se aplica el modelo de Kiani y Shodja (2011) en este trabajo para la representación del avance de los productos de corrosión.

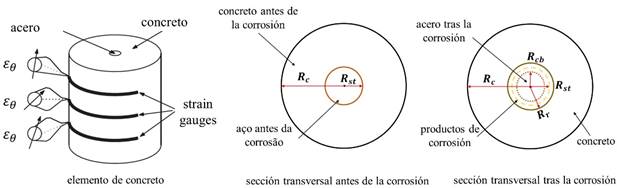
Kiani y Shodja (2011) desarrollaron un modelo lineal para la formación de los productos de corrosión en estructuras de concreto reforzado, usando datos experimentales referentes a probetas cilíndricas de concreto conteniendo en su centro una armadura de diámetro y propriedades físicas conocidas (ver Figura 4).


Figura 4. Representación del modelo de Kiani y Shodja (2011).

El modelo de Kiani y Shodja (2011) se resume en la determinación del radio residual de acero (R_cb) y del radio de frente de avance de los productos de corrosión (R_r), que pueden ser obtenidos respectivamente en (7) y (8). Para la determinación de estos parámetros es necesario calcular el volumen generado por los productos de corrosión, conforme (9), y el volumen de acero perdido por las armaduras, cuya formulación es descrita en (10).

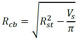(7)

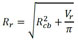(8)

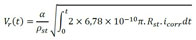(9)

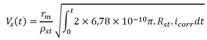(10)

en la que R_st se refiere al radio inicial de la armadura (en m), α es la razón entre la densidad del acero y de los productos de corrosión, ρ_st es la densidad del acero (en kg/m³), r_m es la proporción de masa de hierro y masa molecular de los productos de corrosión, t (en s) se refiere al tiempo de análisis, siendo dado a partir del momento en que ocurre la despasivación de la armadura e i_corr es la densidad de corriente de corrosión natural (en A/m²), calculada de acuerdo a (11).

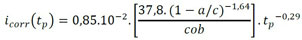(11)

En la que a/c es la relación agua/cemento del concreto, t_p es el tiempo de progresión de la corrosión, período contado después de la despasivación de la armadura (en años), y cob es el espesor del concreto de recubrimiento (en cm).

Cabe mencionar que, al considerar corrosión acelerada, la densidad de corriente es inducida de manera constante y, controlada en laboratorio, siendo impuesta de acuerdo con el tiempo en que el elemento de concreto será analizado y no por (11).

2.3 Acoplamiento de los modelos

Al considerar que la sección transversal de un elemento estructural armado sea representada por un elemento compuesto particulado, conforme se muestra en la Figura 5, la expansión del concreto de recubrimiento debido a la formación de los productos de corrosión es simulada por medio de la expansión de la partícula, una vez que la armadura está perfectamente adherida a la matriz de concreto (condición consecuente de la técnica de embutición adoptada en el acoplamiento).


Figura 5. Representación de la corrosión uniforme vía MEF.

Para que la expansión de la armadura corresponda coherentemente a la expansión causada por los productos de corrosión (ε_r), la deformación del elemento de partícula es determinada por (12), de acuerdo con la medida de deformación de Green.

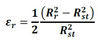(12)

Sin embargo, se observa en la Figura 5 y en (12) que después de iniciado el proceso de corrosión, la dimensión de la partícula que representa la armadura pasa a ser equivalente a la dimensión de la sección de acero en su totalidad más la capa de productos de corrosión, que se forma entre el acero y el concreto. Por lo tanto, es necesario corregir el módulo de elasticidad del elemento de partícula, de forma que sean considerados los efectos de la corrosión en relación con la pérdidada de sección de acero en su totalidad. Para eso, se le considera que el valor del módulo de elasticidad de la partícula es ponderado en función de la pérdida de sección de acero, conforme se describe en (13).

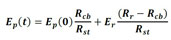(13)

en la que E_p(0) es el módulo de elasticidad inicial de la partícula (referente a la armadura en su totalidad), E_p(t) es el módulo de elasticidad de la partícula en el instante de análisis, E_r es el módulo de elasticidad del producto de corrosión, R_st se refiere al radio inicial de la armadura, R_cb es el radio de acero en su totalidad y R_r es el radio referente al frente de los productos de corrosión.

Para que se le considere una expansión de concreto debido a la formación de los productos de corrosión, se emplea una descomposición aditiva del tensor de deformaciones de Green. Los términos del tensor de deformación de los elementos de partículas son calculados de acuerdo con (14). Se resalta que la descomposición del tensor solo es posible debido a consideración de pequeñas o moderadas deformaciones.

(14)

en la que E_ij representa la porción elástica de la deformación y ε_r es la deformación de la partícula (armadura) debido a la corrosión uniforme para cada una de las direcciones principales.

Mayores detalles acerca del modelo desarrollado, sea de la formulación o de su aplicabilidad, pueden ser obtenidos en Felix (2018).

3. Resultados

A fin de analizar la eficiencia del modelo desarrollado y validarlo, inicialmente se presentan dos simulaciones numéricas referentes a pruebas de laboratorio de elementos de concreto sometidos a corrosión acelerada. Luego, se analizan los efectos de la corrosión uniforme en una estructura de concreto armado por medio del modelo desarrollado. El análisis se hizo considerando dos ambientes, laboratorio (corrosión acelerada) y urbano (corrosión natural).

3.1 Análisis del desempeño y validación del modelo - Ejemplo 1

Para demonstrar la eficiencia del modelo desarrollado vía MEFP para representación de la expansión del concreto debido a la corrosión uniforme, y en especial, de la formación de los productos de corrosión, se presenta inicialmente la modelización de una placa de concreto reforzado bajo corrosión uniforme acelerada, la cual fue experimentalmente analizada por Nguyen et al. (2007).


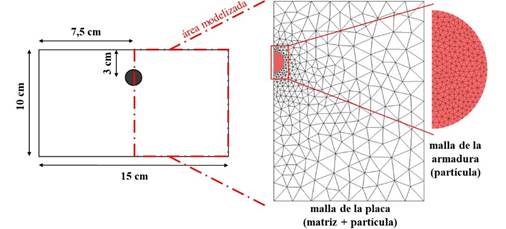
Figura 6. Geometría y discretización empleadas en la modelización.

La placa contiene una armadura con diámetro de 10 mm localizada en la región central, conforme se muestra en la Figura 6 y fue producida con concreto de resistencia a compresión de 39 MPa y acero con límite de proporcionalidad de 500 MPa.

Para lograrse la prueba de corrosión acelerada, Nguyen et al. (2007) sometieron la placa de concreto reforzado, tras curado húmedo de 28 días, a una corriente con densidad constante de 100 µA/cm² por 92 horas.

Para la modelización numérica, solo la mitad de la placa de concreto fue simulada (ver Figura 6), debido a la simetría del problema. La placa fue discretizada por medio de un elemento compuesto particulado, siendo empleados 680 elementos finitos triangulares para la representación de la matriz de concreto y 826 elementos finitos triangulares para la discretización de la armadura.

En la Tabla 1 se presentan los parámetros aplicados para modelización del problema, los cuales fueron extraídos de Nguyen et al. (2007).

Parámetro	Valor	Unidad
Tabla 1. Parámetros de entrada del modelo de corrosión.
Densidad del acero	7860	kg/m³
Valencia	2	-
Razón entre densidad del acero y de los productos de corrosión	3.7	-
Módulo de elasticidad de los productos de corrosión	0.15	GPa
Masa atómica del acero	55.84	-
Razón en volumen de la expansión de los productos de corrosión	3.7	-

Se consideró el comportamiento del concreto como elástico-lineal, con módulo de elasticidad de 25 GPa y coeficiente de Poisson de 0.2. Para el acero, el módulo de elasticidad adoptado fue de 210 GPa y el coeficiente de Poisson de 0.3.

En la Figura 7.a se muestra la deformación medida en un punto situado en la región superior de la placa, obtenida por medio del modelo propuesto y, experimentalmente, en Nguyen et al. (2007).


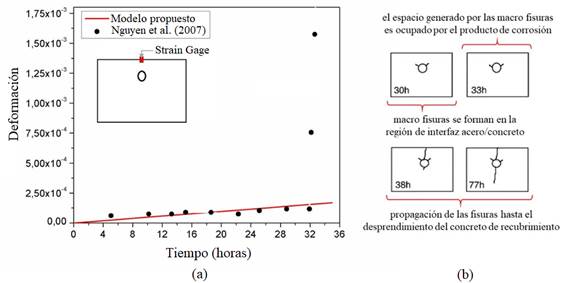
Figura 7. Análisis de la (a) deformación y (b) de la fisuración de la placa de concreto obtenidas por el modelo y comparadas a los resultados experimentales de Nguyen et al. (2007).

Al comparar las deformaciones observadas experimentalmente con las obtenidas por medio del modelo numérico implementado (Figura 7.a), se verificó que el modelo representa coherentemente la expansión del concreto debido a la corrosión uniforme, presentando un desvío medio de 4.12%.

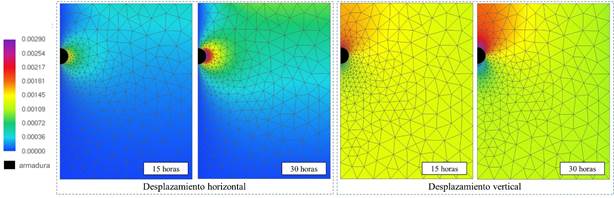
Aún acerca de la Figura 7.a, se observa que después del tiempo de 30 horas, hubo un aumento súbito en la deformación obtenida en Nguyen et al. (2007) y, a partir de ahí el modelo no fue capaz de representar coherentemente las deformaciones impuestas por la corrosión. Eso ocurre pues en este instante macro fisuras se forman en la región de interfaz entre el acero y el concreto, conforme es visto en los mapas de fisuras (Figura 7.b), descritos en Nguyen et al. (2007), para el problema en análisis. Aun así, delante del régimen elástico-lineal del concreto, el modelo describió de forma eficiente las deformaciones impuestas por la corrosión. La Figura 8 ilustra los desplazamientos horizontales y verticales de la placa de concreto tras 15 y 30 horas de corrosión acelerada, donde se muestra que solo a las 30 horas de corrosión deformaciones significativas pueden ser observadas en la superficie del concreto de recubrimiento.


Figura 8. Mapa de colores referente a los campos de desplazamiento (leyenda en cm).


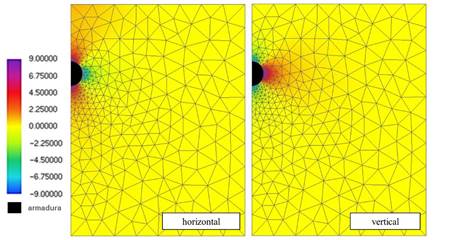
Figura 9. Mapa de colores referente al campo de tensión (leyenda em MPa).

En la Figura 9 se presentan los campos de tensión en la dirección horizontal y vertical de la placa de concreto tras 30 horas de corrosión acelerada. De acuerdo al esperado, se observa (Figura 9) que para el instante de 30 horas de corrosión, las tensiones presentan valores superiores a 3 MPa, lo que corresponde a la resistencia a tracción del concreto y implicaría en probable fisuración, corroborando las conclusiones de Nguyen et al. (2007), vistas en la Figura 7.b.

Por tanto, los resultados obtenidos en la modelización de la placa demuestran que el modelo representa coherentemente los efectos expansivos consecuentes de la corrosión uniforme, delante de la consideración del régimen elástico lineal de los materiales.

3.2 Análisis del desempeño y validación del modelo - Ejemplo 2

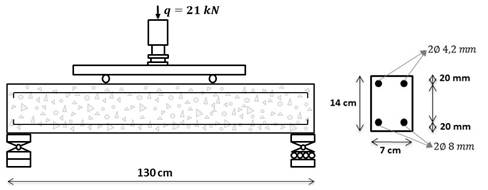
A continuación, para fines de validación del modelo numérico propuesto y considerando el acoplamiento de los modelos mecánicos y del mecanismo de corrosión, se modelizó la degradación impuesta por la corrosión en una viga de concreto reforzado (Figura 10) probada por Graeff (2007). La estructura consiste en un modelo reducido de una viga de sección rectangular, de dimensiones 7x14x130 cm, con luz entre los apoyos de 120 cm. En la Figura 10 se presenta el detallado de la viga y la carga impuesta.


Figura 10. Detallado de la viga de concreto armado.

La discretización de malla de elementos finitos de la viga de concreto reforzado se hizo con 134 nudos y 34 elementos triangulares con orden de aproximación cúbica para la representación de la matriz de concreto y con 340 elementos de triangulares (partículas) para la representación de las armaduras.

En cuanto a las propiedades de los materiales, el concreto posee módulo de elasticidad de 2600.0 kN/cm², resistencia a compresión de 2.5 kN/cm², resistencia a tracción de 0.179 kN/cm² y coeficiente de Poisson de 0.2. Las armaduras, a su vez, poseen módulo de elasticidad de 210 GPa y resistencia a tracción de 500 MPa. En su modelo numérico, Graeff (2007) consideró el comportamiento no lineal del concreto y, como efecto de degradación de la corrosión, la pierda se sección de acero y de adherencia entre el acero y el concreto.


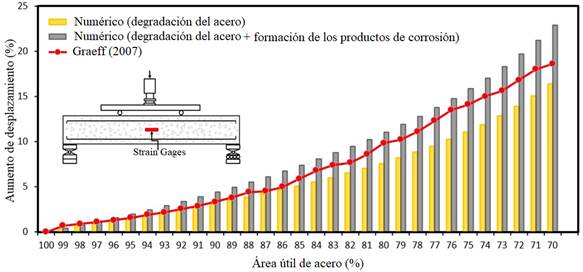
Figura 11. Comparación de desplazamiento máximo experimentado por la viga.

En este trabajo la simulación de la corrosión se hizo considerando dos situaciones, una en que los efectos de corrosión se relacionan solo con la pérdida de sección de acero, y otra en que la corrosión causa la pérdida de sección del acero y la expansión del concreto debido a la formación de productos de corrosión. Por medio de la Figura 11, se comparan los resultados logrados con este trabajo y los determinados en Graeff (2007). Se observa en la Figura 11 que es creciente la diferencia entre los resultados obtenidos por el modelo numérico presentado en este trabajo (en las dos simulaciones) y los obtenidos por Graeff (2007), a medida que aumenta la degradación de las armaduras. Una explicación para tal diferencia se debe al hecho de que Graeff (2007) adopto en su modelo una ley constitutiva no lineal para el concreto y el acero.

Sin embargo, se observa que todas las curvas poseen comportamiento semejante con relación a desplazamientos de la estructura y que considerando el periodo inicial de corrosión (hasta el instante en que la armadura pierde 15% de área útil), para los casos en que los materiales aún trabajan en régimen elástico-lineal, el modelo implementado presenta resultados equivalentes a los de Graeff (2007).

Por medio de la Figura 11 es posible ver que la consideración combinada de más de un efecto de degradación de corrosión resulta en mayores desplazamientos de la viga y que, cuando se considera la expansión del concreto debido a la formación de los productos de corrosión, la pérdida de capacidad mecánica del concreto pasa a ser mayor con el avance de la corrosión. Tal hecho demuestra la importancia de consideración de este fenómeno en la modelización de la corrosión de estructuras de concreto.

3.3 Análisis del campo de desplazamiento de una viga de concreto reforzado sujeta a corrosión

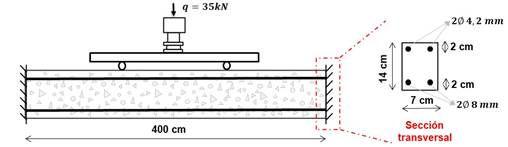
La estructura analizada consiste en una viga biempotrada de concreto reforzado bajo corrosión uniforme. La simulación de esta viga tuvo como objetivo evaluar el efecto de la corrosión uniforme en la deformación de un elemento de concreto armado y sus efectos en los campos de tensión y desplazamiento. La geometría de la viga, sus dimensiones, cargas y condiciones de frontera se presentan en la Figura 12.


Figura 12. Geometría, condiciones de frontera y dimensiones de la viga.

Inicialmente la corrosión es impuesta de forma acelerada, empleando una corriente constante de 100 µA/cm². A continuación, se evalúan los efectos de la corrosión simulada en ambiente de laboratorio (corrosión acelerada) comparándosela con los efectos de la corrosión natural, por medio de una corriente variable en el tiempo, determinada de acuerdo con (11). Los parámetros empleados en la formulación referente a la formación de los productos de corrosión, cuyos datos fueron extraídos de Nguyen et al. (2007) están descritos en la Tabla 1.

La discretización de la malla de elementos finitos de la viga de concreto reforzado se hizo con 2230 nudos y 468 elementos triangulares para la representación de la matriz de concreto y con 952 elementos de triangulares (partículas) para la representación de las armaduras. En cuanto a las propriedades de los materiales, el concreto posee módulo de elasticidad de 2600.0 kN/cm², resistencia a compresión de 2.5 kN/cm², resistencia a tracción de 0.179 kN/cm² y coeficiente de Poisson de 0.2. Las armaduras, por su vez, poseen módulo de elasticidad de 21000 kN/cm² y resistencia a tracción de 50 kN/cm².

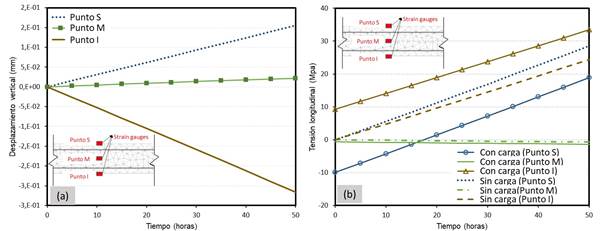
En las Figura 13.a y 13.b se presentan los resultados referentes al desplazamiento vertical y a la tensión longitudinal (para tres diferentes regiones de la viga), considerando las solicitaciones químico-mecánicas (impuestas por la corrosión) y las solicitaciones provenientes de la carga.

Se nota en la Figura 13.a que tras 50 horas de corrosión acelerada, la estructura experimenta un aumento de desplazamiento de 0.26 mm (para bajo) para un punto situado en la parte inferior del centro de la viga (punto “I”), mientras que para un punto situado en la parte superior del centro de la viga (punto “S”), el aumento fue de 0.14 mm, casi la mitad del valor observado en el punto inferior.


Figura 13. Respuestas del modelo para (a) el desplazamiento vertical y (b) tensión longitudinal.

Los resultados presentados en la Figura 13.b demuestran la influencia de la corrosión en el campo de tensión de la viga bajo corrosión cuando considerada la aplicación de una carga externa. Se observa para el caso de solo corrosión (sin carga) que las tensiones en los puntos “S” y “I” son siempre de tracción (independientemente del tiempo de propagación), conforme apuntado por Balafas y Burgoyne (2010). Sin embargo, se nota que, en la presencia de una carga externa, el campo de tensión pasa a tener comportamiento controlado por el nivel de corrosión de las armaduras. Por ejemplo, el punto “S”, situado en la parte superior de la viga, tiene su estado de tensión alterado de compresión para tracción tras 15 horas de corrosión acelerada.

En otras palabras, se ha verificado que existe una influencia significativa de la corrosión en los campos de tensiones de vigas de concreto reforzado en servicio (con carga). Esa influencia tiene efectos secundarios que corroboran con la reducción de la vida útil de las estructuras, a ejemplo, la fisuración del recubrimiento del concreto. El estado de fisuración de un elemento de concreto armado es altamente dependiente de su estado de tensión y, en consecuencia, si la corrosión altera el campo de tensión de un elemento estructural, la misma puede modificar y/o acelerar sus mecanismos de ruptura.

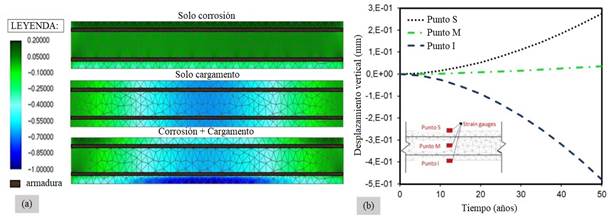
En la Figura 14.a se muestra la configuración deformada de la viga considerando tres diferentes configuraciones de solicitaciones: (i) solo corrosión; (ii) solo carga; y (iii) acción conjunta de carga y corrosión. Se nota que en el caso donde las solicitaciones de la viga son exclusivamente resultado de la corrosión, todo el elemento estructural está traccionado, debido a formación de productos de corrosión. Se observa todavía, que los desplazamientos de la viga para el caso en que hay corrosión y carga externa, pueden ser descritos por sobreposición de las solicitaciones mecánicas (debido a la carga externa) y químico-mecánicas (resultado de la corrosión).

En la Figura 14.b se presentan los resultados para el desplazamiento vertical de la viga de concreto reforzado, considerando solo la corrosión natural.

Delante de los resultados de la simulación de la corrosión natural, los cuales se presentan en la Figura 14.b, se verificó que el desplazamiento del punto “I” tras 50 años de corrosión natural es de 0.47 mm, 79% mayor que el desplazamiento observado tras 50 horas de corrosión acelerada.


Figura 14. (a) Desplazamiento vertical de la viga: (a) a los 50 años y (b) a lo largo del tiempo (mm).

4. Conclusiones

Del análisis de los resultados presentados referentes a la validación del modelo desarrollado, basado en el método de los elementos finitos posicional (MEFP), se puede concluir que el modelo representa coherentemente la expansión del concreto debido a la formación de los productos de corrosión. Además, delante de las simulaciones numéricas se concluye que:

La corrosión tiende a alterar el campo de tensión de un elemento estructural, haciendo que algunas regiones del concreto pasen del estado de compresión a tracción;
La consideración de una carga externa no altera la forma como los productos de corrosión se forman. Por el contrario, los efectos se sobreponen y tienden a ser significativos, a depender del nivel de corrosión de las armaduras;
Los desplazamientos de la viga pueden ser descritos, antes de la fisuración, por la sobreposición de las solicitaciones mecánicas (debido a la carga externa) y químico-mecánicas (de la corrosión);
Existen diferencias en el comportamiento mecánico de un elemento estructural cuando sometido a la corrosión natural o acelerada y la correlación entre los efectos causados por la corrosión en cada uno de los casos no es directa;
Considerando un régimen de pequeñas deformaciones, la sobreposición de los efectos (propiedad muchas veces utilizada para la solución de problemas de estructuras y mecánicas) puede ser extendida para el análisis de la acción de corrosión en armaduras en estructuras de concreto reforzado, en cuanto el daño no sea significativo.

Por último, los resultados demuestran la aplicabilidad del modelo desarrollado como una alternativa viable y eficiente para la simulación de los elementos de concreto reforzado bajo corrosión uniforme, lo que contribuye con los estudios del área de patologías de las construcciones.

5. Agradecimientos

A el “Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq 141078/2018 e CNPq 310564/2018-2)” y a la “Coordenação de Aperfeiçoamento Pessoal de Nível Superior - Brasil (CAPES) com el código de financiación 001” por el apoyo oferecido a la investigación.

6. Referencias

Almusallam, A. A. (2001), Effect of degree of corrosion on the properties of reinforcing steel bars. Construction and Building Materials. 15(8):361-368. https://doi.org/10.1016/S0950-0618(01)00009-5

Andrade, C., Alonso, C., Molina, F. J. (1993), Cover cracking as a function of bar corrosion: Part 1 Experimental test. Materials and Structures. 26:453-464. https://doi.org/10.1007/BF02472805

Balafas, I., Burgoyne, C. J. (2011), Modeling the structural effects of rust in concrete cover. Journal of Engineering Mechanics. Journal of Engineering Mechanics. 137(3):175-185. https://doi.org/10.1061/(ASCE)EM.1943-7889.0000215

Bhargava, K., Ghosh, A. K., Mori, Y., Ramanujam, S. (2005), Modeling of time to corrosion-induced cover cracking in reinforced concrete structures. Cement and Concrete Research. 35(11):2203-2218. https://doi.org/10.1016/j.cemconres.2005.06.007

Coda, H. B. (2018), “O método dos elementos finitos posicional: sólidos e estruturas - Não linearidade geométrica e dinâmica”. Publisher: EESC-USP, Place of publication: São Carlos, SP, p. 284. ISBN: 9788580230680

Du, X., Jin, L. (2014), Meso-scale numerical investigation on cracking of cover concrete induced by corrosion of reinforcing steel. Engineering Failure Analysis. 39:21-33. https://doi.org/10.1016/j.engfailanal.2014.01.011

Felix, E. F. (2018), “Modelagem da deformação do concreto armado devido à formação dos produtos de corrosão”. Master Thesis, Escola de Engenharia de São Carlos/USP, São Carlos.

Gentil, V. (2011), “Corrosão”. Editora LCT, 6º edição, Rio de Janeiro, Brasil, p. 376.

Graeff, A. G. (2007), “Avaliação experimental e modelagem dos efeitos estruturais da propagação da corrosão em elementos de concreto armado”. Master Thesis, Universidade Federal do Rio Grande do Sul, Porto Alegre.

Hansen, E. J., Saouma, V. E. (1999), Numerical simulation of reinforced concrete deterioration: Part 2-steel corrosion and concrete cracking. ACI Materials Journal. 96:331-338. ISSN: 0889-325X.

Helene, P. (1986), “Corrosão em armaduras para concreto armado”. PINI, São Paulo, Brasil. p. 46.

Isgor, O. B., Razaqpur, A. G. (2006), Modelling steel corrosion in concrete structures. Materials and Structures. 39(3):291-302. https://doi.org/10.1007/s11527-005-9022-7

Jiang, L., Lin, B., Cai, Y. (2000), A model for predicting carbonation of high-volume fly ash concrete. Cement and Concrete Research. 30(5):699-702. https://doi.org/10.1016/S0008-8846(00)00227-1

Kiani, K., Shodja, H. M. (2011), Prediction of the penetrated rust into the microcracks of concrete caused by reinforcement corrosion. Applied Mathematical Modelling. 35(5):2529-2543. https://doi.org/10.1016/j.apm.2010.11.039

Liu, Y., Weyers, R. E. (1998), Modeling the time-to-corrosion cracking in chloride contaminated reinforced concrete structures. Materials Journal. 95(6):675-680.

Maruya, T., Hsu, K., Takeda, H., Tangtermsirikul, S. (2003), Numerical modeling of steel corrosion in concrete structures due to chloride ion, oxygen and water movement. Journal of Advanced Concrete Technology. 1(2):147-160. https://doi.org/10.3151/jact.1.147

Mehta, P. K., Monteiro, P. J. M. (2014), “Concreto: microestrutura, propriedades e materiais”. Ibracon, São Paulo, Brasil, p. 751.

Molina, F. J., Alonso, C., Andrade, C. (1993), Cover cracking as a function of bar corrosion: Part 2-Numerical model. Materials and Structures. 26 :532-548. https://doi.org/10.1007/BF02472864

Nguyen, Q. T., Caré, S., Millard, A., Berthaud, Y. (2007), Analyse de la fissuration du béton armé en corrosion accélerée. Comptes Rendus Mecanique. 335(2): 99-104. https://doi.org/10.1016/j.crme.2007.01.005

Ožbolt, J., Oršanić, F., Balabanić, G. (2014), Modeling pullout resistance of corroded reinforcement in concrete: Coupled three-dimensional finite element model. Cement and Concrete Composites. 46:41-55. https://doi.org/10.1016/j.cemconcomp.2013.10.014

Paccola, R. R., Coda, H. B. (2016), A direct FEM approach for particulate reinforced elastic solids. Composite Structures. 45:235-251. https://doi.org/10.1016/j.compstruct.2016.01.062

Paul, S. C., Zijl, G. P. A. G. V. (2016), Chloride-induced corrosion modelling of cracked reinforced SHCC. Archives of Civil and Mechanical Engineering. 16(4):734-742. https://doi.org/10.1016/j.acme.2016.04.016

Ribeiro, D., Cunha, M., Helene, P. (2015), “Corrosão em Estruturas de Concreto Armado: Teoria, Controle e Métodos de Análise”. Elsevier Brasil, Campus, São Paulo, Brasil, p. 272.

Vanalli, L., Paccola, R. R., Coda, H. B. (2008), A simply way to introduce fibers into FEM models. Communications in Numerical Methods in Engineering. 24:585-603. https://doi.org/10.1002/cnm.983

Yuan, Y., Ji, Y. (2009), Modeling corroded section configuration of steel bar in concrete structure. Construction and Building Materials. 23(6):2461-2466. https://doi.org/10.1016/j.conbuildmat.2008.09.026

Zhu, W. (2014), “Effect of corrosion on the mechanical properties of the corroded reinforcement and the residual structural performance of the corroded beams”, Doctoral Dissertation, Institut National des Sciences Appliquées de Toulouse (INSA de Toulouse).