Pesquisa Básicahttps://doi.org/10.21041/ra.v10i3.395

Desenvolvimento e análise de um modelo numérico da expansão do concreto armado sujeito à corrosão uniforme

Development and analysis of a numerical model of the reinforced concrete expansion due to uniform corrosion

Desarrollo y análisis de un modelo numérico de expansión de concreto reforzado sujeto a corrosión uniforme

E. F. Felix1 * , R. Carrazedo1 , E. Possan2 , E. S. Ramos1

1 University of São Paulo at São Carlos School of Engineering, Brasil.

2 Universidade Federal da Integração Latino-Americana (UNILA), Brasil.

*Autor de Contato: emerson.felipe.felix@gmail.com

Recepção: 21 de fevereiro de 2019.
Aceitação: 11 de dezembro de 2019.
Publicação: 31 de agosto de 2020.


Citar como: Felix, E. F., Carrazedo, R., Possan, E., Ramos, E. S. (2020), "Desenvolvimento e análise de um modelo numérico da expansão do concreto armado sujeito à corrosão uniforme", Revista ALCONPAT, 10 (3), pp. 300 – 316, DOI: https://doi.org/10.21041/ra.v10i3.395

Resumo
Este trabalho apresenta a modelagem e análise dos efeitos da corrosão por carbonatação em elementos de concreto armado através de um modelo numérico baseado no Método dos Elementos Finitos. Para controlar e minimizar os danos associados à corrosão faz-se necessário deter ferramentas e conhecimento suficientes para entender os efeitos desta manifestação patológica sobre o comportamento mecânico do concreto armado. Diante dos resultados obtidos, constatou-se que a depender do nível de corrosão das armaduras, o elemento de concreto tem seu estado de tensão e deformação comprometido. Ademais, os resultados apontam a eficiência do modelo desenvolvido e a sua aplicabilidade frente à simulação do comportamento mecânico de estruturas de concreto armado sujeitas à corrosão uniforme.
Palavras-chave: concreto armado, corrosão, modelagem numérica, método dos elementos finitos.

Abstract
This paper presents the modeling and analysis of the corrosion effects due to carbonation on reinforced concrete elements through a numerical model based on the Finite Element Method. In order to minimize corrosion damage, tools are required to understand the pathological manifestation on the mechanical behavior of reinforced concrete. It was found that depending on the reinforcement corrosion stage, the state of stress and deformation of the concrete element is compromised. Besides, results show the efficiency of the developed model and its applicability to the simulation of the mechanical behavior of reinforced concrete structures subjected to uniform corrosion.
Keywords: reinforced concrete, corrosion, numerical modeling, finite element method.

Resumen
Este trabajo presenta la modelización y análisis de los efectos de la corrosión por carbonatación en elementos de concreto reforzado a través de un modelo numérico basado en el Método de los Elementos Finitos. Para controlar y minimizar el daño asociado a la corrosión se hace necesario disponer de herramientas y conocimientos suficientes para comprender los efectos de esta manifestación patológica sobre el comportamiento mecánico del concreto reforzado. Ante los resultados obtenidos, se constató que, dependiendo del nivel de corrosión de las armaduras, el elemento de concreto tiene su estado de tensión y deformación alterado. Además, los resultados indican la eficiencia del modelo desarrollado y su aplicabilidad frente a la simulación del comportamiento mecánico del concreto reforzado con corrosión uniforme.
Palabras clave: concreto reforzado, corrosión, modelización numérica, método de los elementos finitos.


1. Introdução

A degradação de estruturas de concreto armado devido à ação da corrosão das armaduras é de difícil mensuração devido à complexidade do fenômeno físico-químico e dos múltiplos parâmetros envolvidos (Mehta e Monteiro, 2014). Do ponto de vista da mecânica dos materiais e das estruturas, o principal efeito da corrosão às armaduras consiste na perda de massa do aço e, por consequência, na transformação desse material nos produtos de corrosão, ou ferrugem, como é vulgarmente conhecido. Os produtos da corrosão possuem natureza expansiva, gerando tensões de tração no interior do concreto que levam a fissuração e o destacamento do concreto ao longo do tempo.

Em geral, o concreto apresenta condições suficientes para a proteção das armaduras contra a corrosão, graças a alta alcalinidade da pasta (pH situado entre 12 e 13). Entretanto, esta proteção é perdida à medida em que o concreto está sujeito pelos diferentes agentes agressivos presentes na atmosfera, por exemplo, íons de cloreto (Cl-) e dióxido de carbono (CO2) (Gentil, 2011).

A depender da concentração do agente agressivo, presente na atmosfera, o processo corrosivo pode ser classificado como uniforme ou localizado. A corrosão localizada ou por pite ocorre quando íons cloretos causam um aumento da condutividade elétrica do concreto e atacam a camada passivadora que protege as armaduras. Neste tipo de corrosão apenas algumas regiões da armadura perdem massa de aço, justificando o termo "localizada", utilizado em sua classificação (Ribeiro et al., 2015).

O processo corrosivo é dito uniforme ou por carbonatação quando o teor de CO2 presente na atmosfera é preponderante ao de íons cloretos. Neste caso, a difusão do CO2 no concreto causa a diminuição do pH da matriz cimentícia (de aproximadamente 13 ou 12 até 9), o que leva a destruição da camada passivadora que envolve as armaduras, tornando o aço susceptível à corrosão (Mehta e Monteiro, 2014).

A corrosão uniforme ocorre predominantemente em estruturas com concreto de baixa qualidade, em locais onde o cobrimento da armadura é insuficiente para garantir a proteção do aço ou em ambientes de severa agressividade (Ribeiro et al., 2015). Helene (1986) verificou que, nestes casos, a corrosão leva à formação de produtos de corrosão na interface entre o aço e o concreto, e que estes podem ocupar um espaço de 3 a 10 vezes maior que o inicial.

De acordo com Andrade et al. (1993) e Ribeiro et al. (2015), a formação e o desenvolvimento dos produtos de corrosão, devido à corrosão uniforme, dependem de diversos fatores, sejam eles ambientais (temperatura do ambiente, umidade relativa do ar, grau de agressividade do ambiente, teor de exposição ao CO2, entre outros) ou construtivos (tipo de cimento utilizado na produção do concreto, relação água/cimento do concreto, tipo de aço, dimensão do cobrimento das armaduras, entre outros).

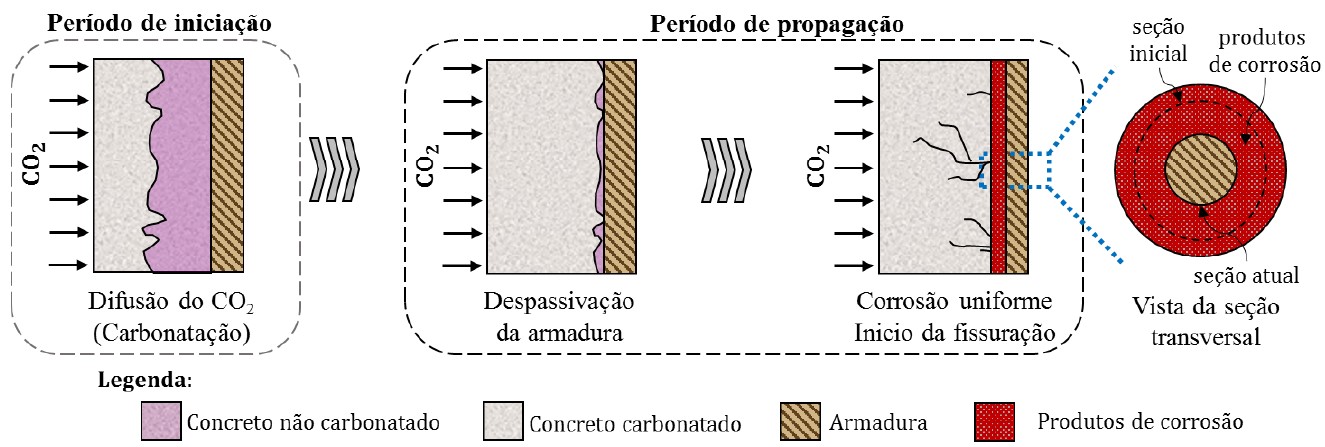
Com a formação dos produtos de corrosão, campos internos de tensão são gerados na interface entre o aço e concreto. A medida em que as tensões geradas pelos produtos de corrosão se tornam superiores às resistidas pelo concreto, microfissuras surgem na matriz de concreto que, com a progressão da manifestação patológica, aumentam de tamanho e espessura, espalhando-se por todo o elemento estrutural até causar o destacamento do concreto de cobrimento, afetando a durabilidade e reduzindo a vida útil da estrutura. O processo de degradação é apresentado na Figura 1.

Figura 1. Evolução da corrosão no concreto.

A fim de minimizar os efeitos da corrosão é necessário conhecer as formas de iniciação e propagação do processo corrosivo, possibilitando a redução de sua incidência e, em casos avançados, a reparação e/ou restauração das estruturas de forma a aumentar a sua vida útil, reduzindo riscos e danos aos seus usuários.

Para o estudo da corrosão e de seus efeitos no comportamento mecânico do concreto armado, alguns trabalhos experimentais foram realizados (Molina et al., 1993; Almusallam, 2001; Graeff, 2007; Zhu, 2014), os quais resultaram em descobertas relevantes para a área. Entretanto, três importantes limitações são apontadas pelos pesquisadores: (i) a dificuldade de estudar isoladamente os diferentes fatores que influenciam no processo de corrosão; (ii) elevados custos e (iii) tempo necessário para a realização dos ensaios experimentais.

Com o avanço da computação, diversas ferramentas numéricas foram desenvolvidas, à exemplo, o Método dos Elementos de Contorno (MEC), o Método dos Elementos Finitos (MEF), Redes Neurais Artificiais (RNA), entre outras, fazendo com que pesquisadores da área e as utilizassem para a criação de modelos numéricos, uma vez que estas ferramentas se apresentam como uma alternativa eficiente para a superação dos limites anteriormente citados.

Sabendo disso, Hansen e Saouma (1999), Maruya et al. (2003) e Bhargava et al. (2005) utilizaram diferentes ferramentas numéricas para a resolução de forma automatizada de equações matemáticas referentes aos mecanismos da corrosão, o que possibilitou analisar os efeitos da corrosão e sua propagação. Procedimentos semelhantes foram adotados por Isgor e Razaqpur (2006), Xu et al. (2009), Du e Jin (2014), Ožbolt et al. (2014) e Paul e Zijl (2016), porém os autores resolveram o problema químico-mecânico, referente à corrosão em elementos de concreto armado, via Método dos Elementos Finitos.

Assim, dando continuidade à utilização de ferramentas numéricas para o estudo da corrosão e seus efeitos, no presente trabalho é apresentado e analisado um modelo numérico desenvolvido via Método dos Elementos Finitos Posicional (MEFP). O modelo desenvolvido possibilita a simulação da expansão do concreto armado devido à corrosão uniforme e, em especial, à formação dos produtos de corrosão.


2. Modelo da expansão do concreto devido à corrosão

2.1 Modelo mecânico

Com o objetivo de simular a expansão do concreto armado devido à corrosão uniforme, em especial, à formação dos produtos de corrosão, desenvolveu-se uma ferramenta numérica baseada no Método dos Elementos Finitos Posicional (MEFP). O código foi desenvolvido em linguagem Fortran e considera diferentes formulações analíticas para a determinação de parâmetros representativos da corrosão.

Para a determinação do comportamento mecânico do concreto armado, utilizou-se uma formulação baseada no MEFP para sólidos compósitos, desenvolvida incialmente por Vanalli et al. (2008) e recentemente expandida em Paccola e Coda (2016), onde os parâmetros nodais considerados são as posições e as deformações são medidas em relação à posição inicial do corpo. A medida de deformação é a de Green e a lei constitutiva dos materiais é a de Saint-Venant-Kirchhoff.

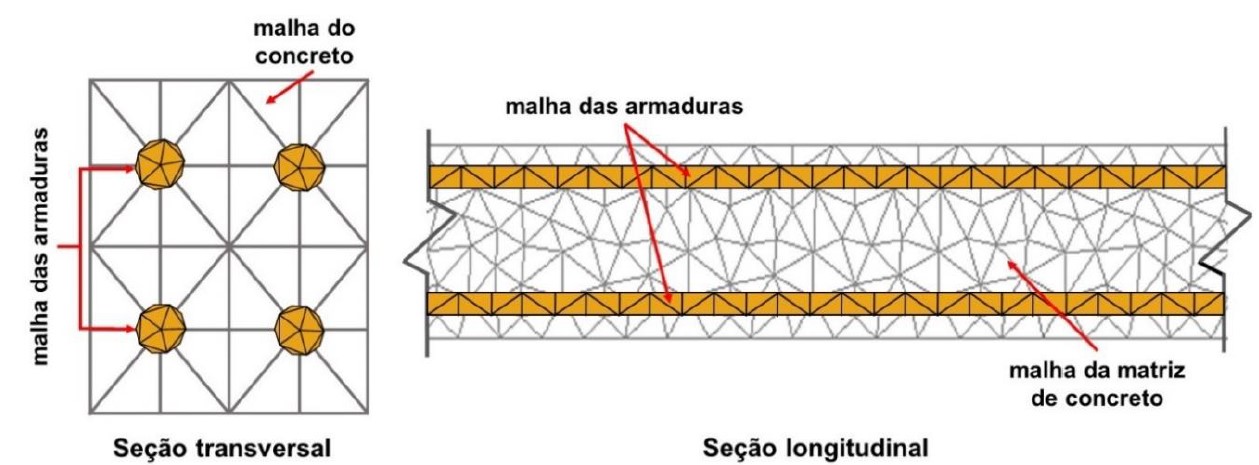
Figura 2. Discretização da seção transversal e longitudinal de uma viga de concreto armado.

O concreto armado é discretizado levando em consideração a matriz de concreto e as armaduras (Figura 2). Tanto a matriz de concreto quanto as armaduras são representadas por meio de elementos finitos bidimensionais triangulares planos, sendo a malha das armaduras acoplada à da matriz de concreto por meio da técnica do embutimento, descrita em Vanalli et al. (2008) e Paccola e Coda (2016). Neste caso há perfeita aderência entre a partícula e a matriz, fazendo com que a utilização de elementos de partículas não aumente os graus de liberdade do sistema. Todos os graus de liberdade dos elementos de partículas são escritos em função dos elementos da matriz.

Na sequência é apresentado de forma sucinta o processo empregado neste trabalho para a obtenção da resposta mecânica de um problema via MEFP para o concreto armado.

Considerando-se forças conservativas e o Princípio da Mínima Energia Potencial Estacionária para a solução do problema não linear geométrico, a energia potencial total de um sólido compósito particulado é dada em (1).

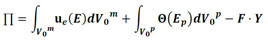(1)

em que Θ é a energia específica de deformação das partículas, ue é a energia específica de deformação da matriz, F é o vetor de forças conservativas externas, Y é o vetor de posição nodal, Ep é a deformação desenvolvida nas partículas, calculada por (2), E é a deformação desenvolvida na matriz, também calculada conforme (2), e V0p e V0m representam os volumes iniciais das partículas e da matriz, respectivamente.

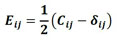(2)

em que Eij representa a parcela elástica da deformação, Cij é o tensor de alongamento à direita de Cauchy-Green e δij representa o delta de Kronecker.

Considerando que a variação da energia potencial total é igual a zero na configuração de equilíbrio, o problema consiste em encontrar o vetor de posição nodal que remete à essa posição, conforme apresentado em (3).

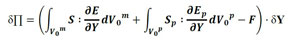(3)

em que S é o segundo tensor de tensões de Piola-Kirchhoff desenvolvido na matriz elástica e Sp é o segundo tensor de tensões de Piola-Kirchhoff desenvolvido nas partículas.

A solução de (3) é obtida por meio do processo iterativo de Newton-Raphson, o qual utiliza como estratégia de solução um vetor de desbalanceamento de forças g, conforme apresentado em (4).

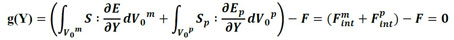(4)

em que Fmint é o vetor de forças internas da matriz e Fpint é o vetor de forças internas das partículas. Como o processo é não linear, expande-se (4) por série de Taylor, conforme descrito em (5).

  (5)

em que Y é uma posição tentativa e H é a matriz Hessiana (ou matriz de rigidez tangente).

Como as forças são conservativas, H pode ser 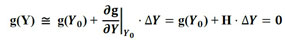decomposta em duas matrizes, uma referente a contribuição da rigidez dos elementos da matriz (Hm) e outra dos elementos de partículas (Hp), como descrito em (6).

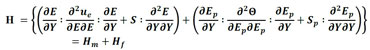(6)

A solução do sistema não linear apresentado em (5) pelo método de Newton-Raphson fornece a correção da posição (Y = Y0+ ∆Y) e o procedimento é repetido até que |∆Y|/|X| seja menor do que uma dada tolerância X é o vetor das posições nodais da configuração inicial.

Maiores detalhes acerca das deduções das equações aqui descritas, assim como do processo de acoplamento dos elementos de partícula à matriz, podem ser vistos em Paccola e Coda (2016) e Coda (2018).

2.2 Modelo de corrosão

Entender como se desenvolvem e se distribuem os produtos de corrosão ao redor da seção da armadura possibilita a determinação de modelos e ferramentas que são capazes de descrever os campos de deformação e de tensão que surgem nas estruturas de concreto armado sujeitas à corrosão. Estes modelos auxiliam nos estudos referentes aos efeitos da corrosão sobre o comportamento mecânico do concreto, da durabilidade e vida útil destas estruturas.

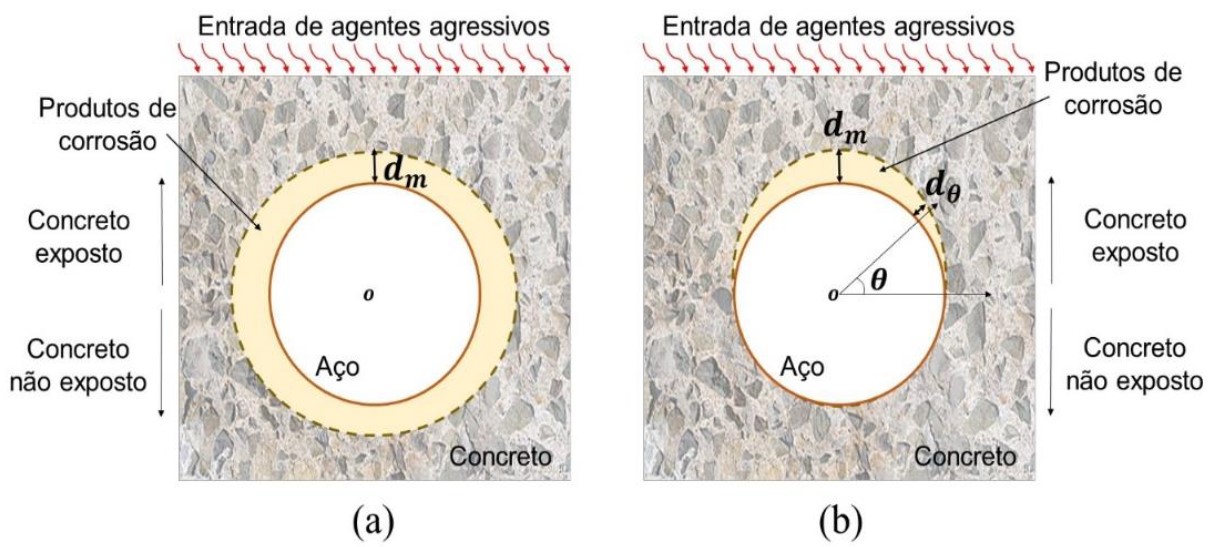
Ao longo dos últimos anos alguns modelos foram propostos com objetivo de representar e descrever o perfil de distribuição dos produtos de corrosão no entorno das armaduras, à exemplo, Liu e Weyers (1998), Yuan e Ji (2009), Balafas e Burgoyne (2010) e Kiani e Shodja (2011). Quanto ao perfil da formação e distribuição dos produtos de corrosão, eles são divididos em linear e não linear, conforme apresentado na Figura 3.

Figura 3. Perfil de formação dos produtos de corrosão: (a) linear e (b) não linear.

Assim, considerando que a corrosão desencadeada pela carbonatação do concreto de cobrimento se desenvolve uniformemente em toda a armadura, o modelo de Kiani e Shodja (2011) é utilizado neste trabalho para a representação do avanço dos produtos de corrosão.

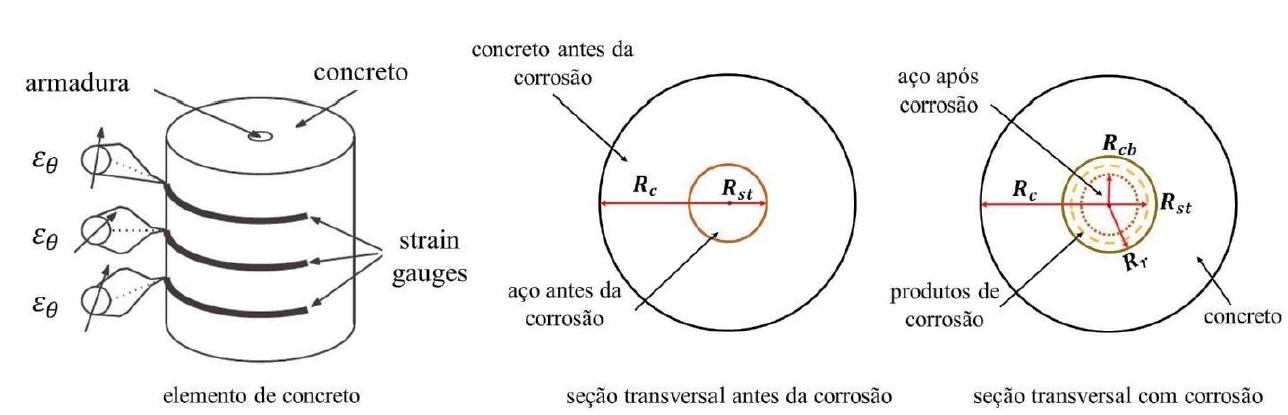
Kiani e Shodja (2011) desenvolveram um modelo linear para a formação dos produtos de corrosão em estruturas de concreto armado, utilizando dados experimentais referentes a corpos de prova cilíndricos de concreto contendo em seu centro uma armadura de diâmetro e propriedades físicas conhecidas (ver Figura 4).

Figura 4. Representação do modelo de Kiani e Shodja (2011).

O modelo de Kiani e Shodja (2011), resume-se na determinação do raio residual de aço (Rcb) e do raio da frente de avanço dos produtos de corrosão (Rr), que podem ser obtidos respectivamente em (7) e (8). Para a determinação destes parâmetros faz-se necessário calcular o volume gerado pelos produtos de corrosão, conforme (9), e o volume de aço que as armaduras perderam, cuja formulação é descrita em (10).

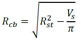(7)
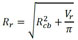(8)
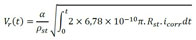(9)
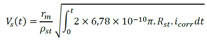(10)

em que Rst refere-se ao raio inicial da armadura (em m), α é a razão entre a densidade do aço e dos produtos de corrosão, ρst é a densidade do aço (em kg/m³),rm é a proporção de massa de ferro para a massa molecular dos produtos de corrosão, t (em s) refere-se ao tempo de análise, sendo dado a partir do momento em que ocorre a despassivação da armadura e icorr é a densidade da corrente de corrosão natural (em A/m²), calculada de acordo com (11).

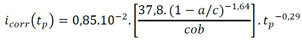(11)

em que a/c é a relação água/cimento do concreto, tp é o tempo de progressão da corrosão, período contado após a despassivação da armadura (em anos), e cob é a espessura do concreto de cobrimento (em cm).

Cabe mencionar que ao considerar corrosão acelerada, a densidade de corrente é induzida de forma constante e, controlada em laboratório, sendo imposta de acordo com o tempo em que o elemento de concreto será analisado e não por (11).

2.3 Acoplamento dos modelos

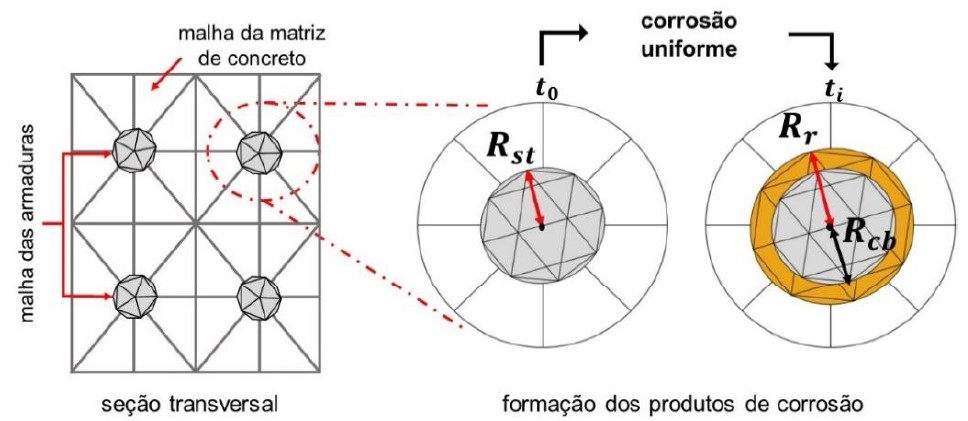
Considerando que a seção transversal de um elemento estrutural de concreto armado seja representada por um elemento compósito particulado, conforme mostra a Figura 5, a expansão do concreto de cobrimento devido à formação dos produtos de corrosão, é simulada por meio da expansão do elemento de partícula, uma vez que a armadura está perfeitamente aderida à matriz de concreto (condição decorrente da técnica de embutimento adotada no acoplamento).

Figura 5. Representação da corrosão uniforme via MEF.

Para que a expansão da armadura corresponda coerentemente à expansão causada pelos produtos de corrosão (εr), a deformação do elemento de partícula é determinada por (12), de acordo com a medida de deformação de Green.

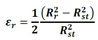(12)

Entretanto, observa-se na Figura 5 e em (12) que, após iniciado o processo de corrosão, a dimensão da partícula que representa a armadura passa a ser equivalente à dimensão da seção integra de aço mais a camada de produtos de corrosão, que se forma entre o aço e o concreto. Assim, faz-se necessário corrigir o módulo de elasticidade do elemento de partícula, de forma que sejam inseridos os efeitos da corrosão no que diz respeito à perda de seção integra de aço. Para isso, considera-se que o valor do módulo de elasticidade da partícula é ponderado em função da perda de seção de aço, conforme descrito em (13).

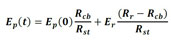(13)

em que Ep(0) é o módulo de elasticidade inicial da partícula (referente à armadura integra), Ep(t) é o módulo de elasticidade da partícula no instante de análise, Er é o módulo de elasticidade do produto de corrosão, Rst refere-se ao raio inicial da armadura, Rcb é o raio integro de aço e Rr é o raio referente à frente dos produtos de corrosão.

Por fim, para que seja considerada a expansão do concreto devido à formação dos produtos de corrosão, emprega-se uma decomposição aditiva do tensor de deformações de Green. Assim, os termos do tensor de deformação dos elementos de partículas são calculados de acordo com (14). Cabe mencionar que a decomposição do tensor só é possível devido a consideração de pequenas ou moderadas deformações.

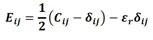(14)

em que Eij representa a parcela elástica da deformação e εr é a deformação da partícula (armadura) devido à corrosão uniforme para cada uma das direções principais.

Maiores detalhes acerca do modelo desenvolvido, seja da formulação ou da sua aplicabilidade, podem ser obtidos em Felix (2018).


3. Resultados

A fim de analisar a eficiência do modelo desenvolvido e validá-lo, incialmente, são apresentadas duas simulações numéricas referentes a ensaios laboratoriais de elementos de concreto submetidos à corrosão acelerada. Em seguida, analisam-se os efeitos da corrosão uniforme em uma estrutura de concreto armado por meio do modelo desenvolvido. A análise foi realizada considerando dois ambientes, laboratório (corrosão acelerada) e urbano (corrosão natural).

3.1 Análise do desempenho e validação do modelo - Exemplo 1

A fim de demonstrar a eficiência do modelo desenvolvido via MEFP para a representação da expansão do concreto devido à corrosão uniforme, e em especial, da formação dos produtos de corrosão, apresenta-se inicialmente a modelagem de uma placa de concreto armado sob corrosão uniforme acelerada, à qual foi experimentalmente analisada por Nguyen et al. (2007).

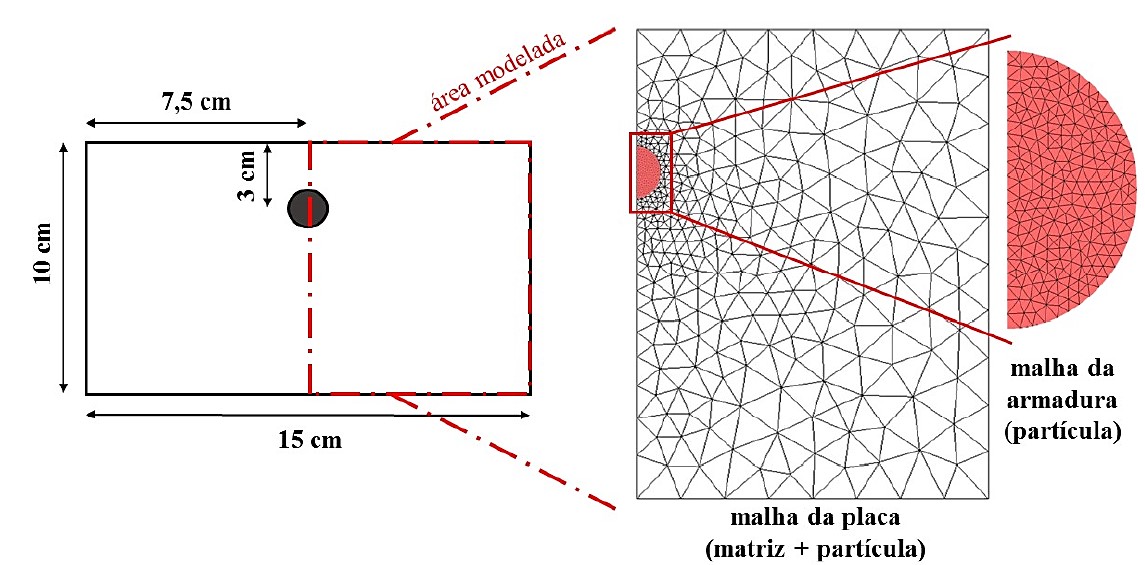
Figura 6. Geometria e discretização utilizada na modelagem.

A placa contém uma armadura com diâmetro de 10 mm localizada na região central, conforme mostra a Figura 6. A placa foi produzida com um concreto de resistência à compressão de 39 MPa e aço com limite de escoamento de 500 MPa.

Para a realização do ensaio de corrosão acelerada, Nguyen et al. (2007) submeteram a placa de concreto armado, após cura úmida de 28 dias, à uma corrente com densidade constante de 100 µA/cm², durante 92 horas.

Para a modelagem numérica, apenas metade da placa de concreto foi simulada (ver Figura 6), devido a simetria do problema. A placa foi discretizada por meio de um elemento compósito particulado, sendo utilizados 680 elementos finitos triangulares para a representação da matriz de concreto e, 826 elementos finitos triangulares para a discretização da armadura.

A Tabela 1 apresenta os parâmetros utilizados para a modelagem do problema, os quais foram extraídos de Nguyen et al. (2007).

Tabela 1. Parâmetros de entrada do modelo de corrosão
Parâmetro Valor Unidade
Densidade do aço 7860 kg/m³
Valência 2 -
Razão entre densidade do aço e dos produtos de corrosão 3.7 -
Módulo de elasticidade dos produtos de corrosão 0.15 GPa
Massa atômica do aço 55.84 -
Razão em volume da expansão dos produtos de corrosão 3.7 -

O comportamento do concreto foi considerado elástico-linear, com módulo de elasticidade de 25 GPa e coeficiente de Poisson de 0.2. Para o aço, o módulo de elasticidade adotado foi de 210 GPa e coeficiente de Poisson de 0.3.

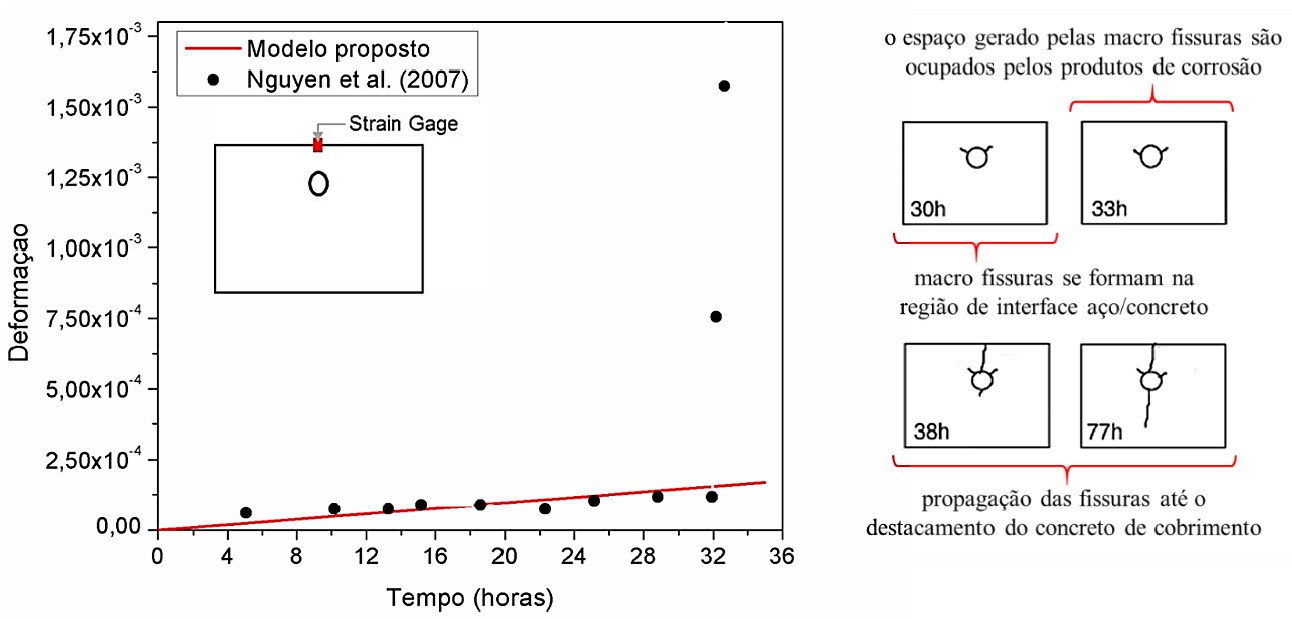
Na Figura 7.a é apresentada a deformação medida em um ponto situado na região superior da placa, obtida por meio do modelo proposto e, experimentalmente, em Nguyen et al. (2007).

Figura 7. Análise da (a) deformação e (b) da fissuração da placa de concreto obtidas pelo modelo comparadas ao experimental de Nguyen et al. (2007).

Comparando as deformações observadas experimentalmente e as obtidas por meio do modelo numérico implementado (Figura 7.a), verificou-se que o modelo representa coerentemente a expansão do concreto devido à corrosão uniforme, apresentando um desvio médio foi de 4.12 %.

Ainda sobre a Figura 7, observa-se que após o tempo de 30 horas, houve um aumento súbito na deformação obtida em Nguyen et al. (2007), momento em que modelo não foi capaz de representar coerentemente as deformações impostas pela corrosão. Isso ocorre, pois neste instante macro fissuras se formam na região de interface entre o aço e o concreto, conforme é visto nos mapas de fissuras (Figura 7.b), descritos em Nguyen et al. (2007), para o problema em análise. Assim, perante o regime elástico-linear do concreto, o modelo descreveu de forma eficiente as deformações impostas pela corrosão.

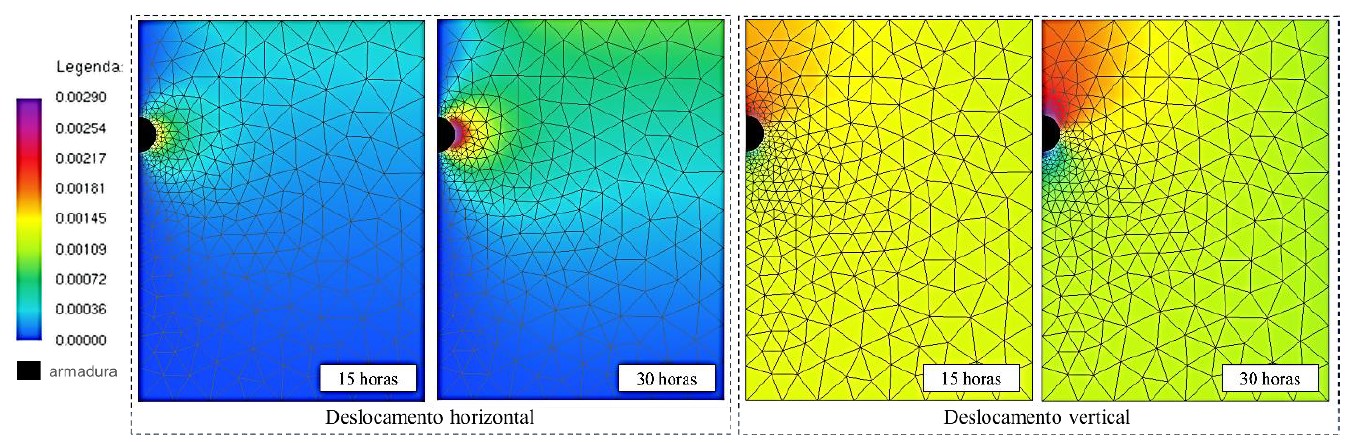
A Figuras 8 ilustra os deslocamentos horizontal e vertical, da placa de concreto após 15 e 30 horas de corrosão acelerada, onde é possível observar que só às 30 horas de corrosão, deformações significativas podem ser observadas na superfície do concreto de cobrimento.

Figura 8. Mapa de cores referente aos campos de deslocamento (legenda em cm).
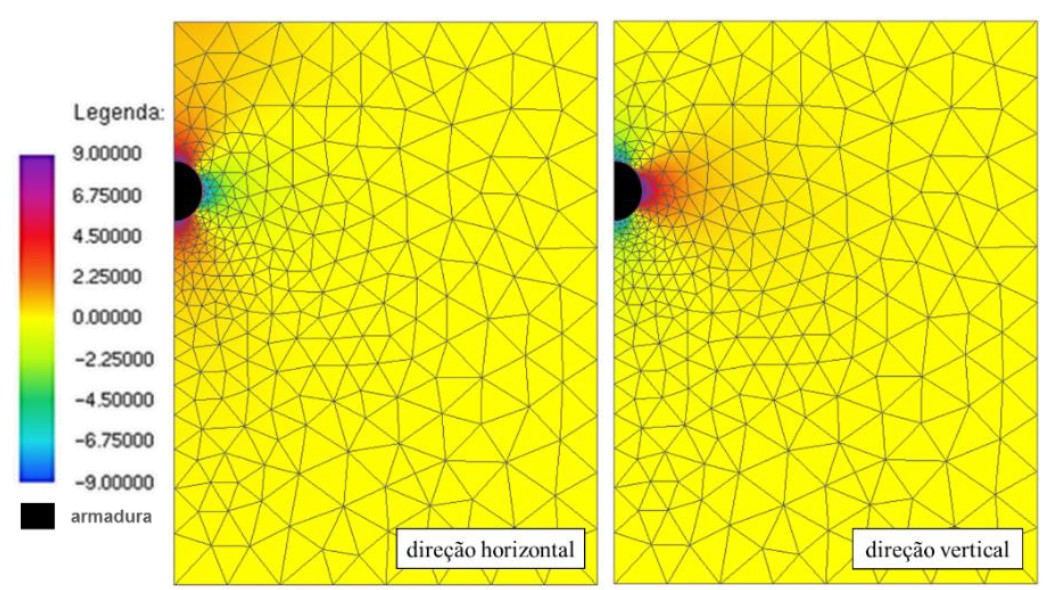
Figura 9. Mapa de cores referente ao campo de tensão (legenda em MPa).

A Figura 9 apresenta os campos de tensão na direção horizontal e vertical da placa de concreto após 30 horas de corrosão acelerada. Como esperado, é possível observar (Figuras 9) que, para o instante de 30 horas de corrosão, as tensões de tração apresentam valores superiores a 3 MPa, valor correspondente à resistência à tração do concreto, o que implicaria em provável surgimento de fissuras, corroborando as conclusões de Nguyen et al. (2007), vistas na Figura 7.b.

Assim, os resultados obtidos na modelagem da placa demonstram que o modelo representa coerentemente os efeitos expansivos decorrentes da corrosão uniforme, diante da consideração do regime elástico linear dos materiais.

3.2 Análise do desempenho e validação do modelo - Exemplo 2

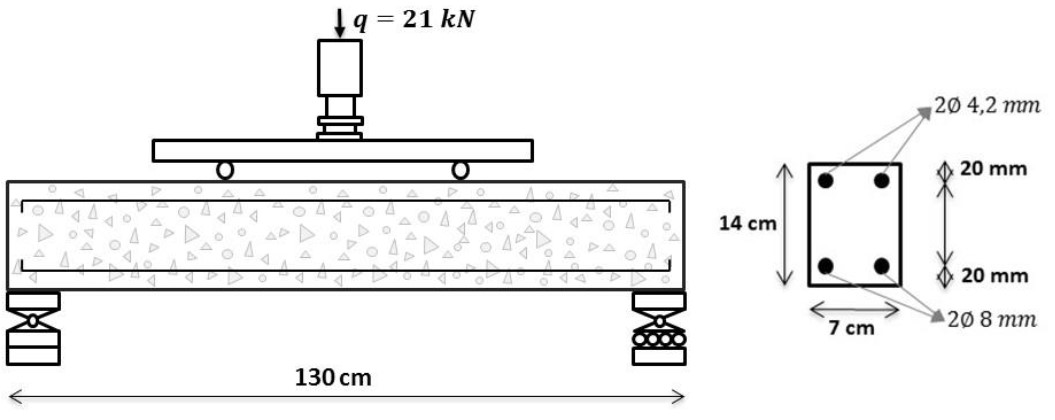
Em seguida, para fins de validação do modelo numérico proposto, considerando o acoplamento dos modelos mecânico e do mecanismo de corrosão, modelou-se a degradação imposta pela corrosão em uma viga de concreto armado (Figura 10) ensaiada por Graeff (2007). A estrutura consiste em um modelo reduzido de uma viga de seção retangular, de dimensão 7x14x130 cm, com vão entre os apoios de 120 cm. Na Figura 10 é apresentado o detalhamento da viga e o carregamento imposto.

Figura 10. Detalhamento da viga de concreto armado.

A discretização da malha de elementos finitos da viga de concreto armado foi feita com 134 nós e 34 elementos triangulares com ordem de aproximação cúbica para a representação da matriz de concreto, e com 340 elementos de triangulares (partículas) para a representação das armaduras.

Quanto às propriedades dos materiais, o concreto possuí módulo de elasticidade de 2600.0 kN/cm², resistência à compressão de 2.5 kN/cm², resistência à tração de 0.179 kN/cm² e coeficiente de Poisson de 0.2. Já as armaduras possuem módulo de elasticidade 210 GPa e resistência à tração de 500 MPa.

Em seu modelo numérico, Graeff (2007) considerou o comportamento não linear do concreto e, como efeitos de degradação da corrosão, a perda de seção de aço e de aderência entre o aço e o concreto.

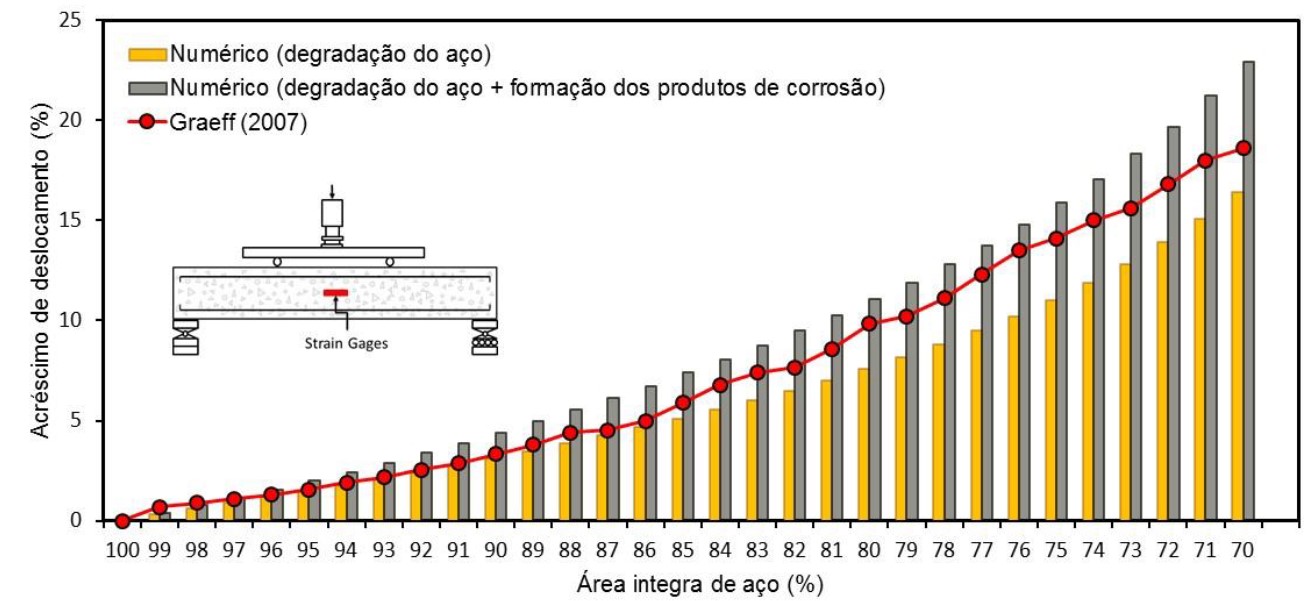
Figura 11. Comparação do deslocamento máximo experimentado pela viga.

Neste trabalho a simulação da corrosão foi feita considerando duas situações, uma em que os efeitos da corrosão remetem apenas à perda de seção de aço, e outra, em que a corrosão causa a perda de seção de aço e a expansão do concreto devido à formação de produtos de corrosão. Por meio da Figura 11, os resultados obtidos neste trabalho e os determinados em Graeff (2007), são comparados.

Observa-se pela Figura 11 que é crescente a diferença entre os resultados obtidos pelo modelo numérico apresentado neste trabalho (nas duas simulações) e os obtidos por Graeff (2007), à medida que aumenta a degradação das armaduras. Uma explicação para tal diferença deve-se ao fato de Graeff (2007) adotar em seu modelo uma lei constitutiva não-linear para o concreto e o aço.

Entretanto, observa-se que todas as curvas possuem comportamento semelhante no que diz respeito a deslocabilidade da estrutura, e que, se considerado o período inicial da corrosão (até o instante em que a armadura perde 15% de área útil), ou momento em que os materiais ainda trabalham em regime elástico-linear, o modelo implementado apresenta resultados equivalentes aos de Graeff (2007).

Por meio da Figura 11 é possível ver que a consideração combinada de mais de um efeito de degradação da corrosão acarreta em uma maior deslocabilidade da viga, e que, quando considerada a expansão do concreto devido à formação dos produtos de corrosão, a perda da capacidade mecânica do concreto passa a ser maior com o avanço da corrosão. Tal fato demonstra a importância da consideração deste fenômeno na modelagem da corrosão de estruturas de concreto.

3.3 Análise do campo de deformação de uma viga de concreto armado sujeita à corrosão

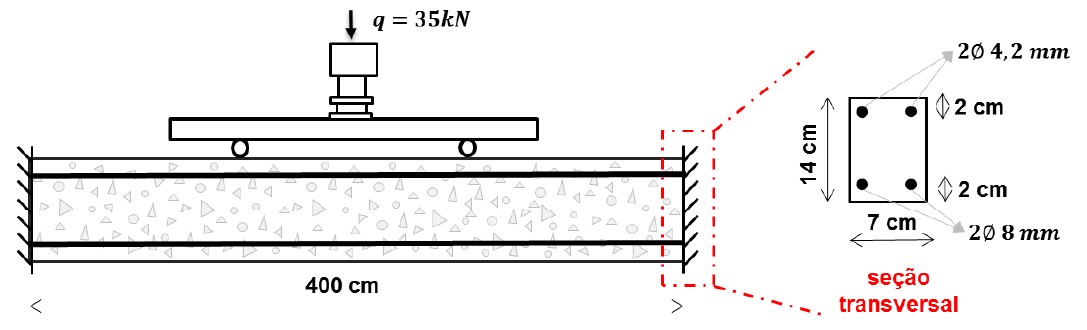
A estrutura analisada consiste em uma viga bi engastada de concreto armado sob corrosão uniforme. A simulação desta viga tem por objetivo avaliar o efeito da corrosão uniforme na deformação de um elemento de concreto armado e seus efeitos nos campos de tensão e deslocamento. A geometria da viga, suas dimensões, carregamento e condições de contorno são apresentadas na Figura 12.

Figura 12. Geometria, condições de contorno e dimensões da viga.

Inicialmente a corrosão é imposta de forma acelerada, utilizando uma corrente constante de 100 µA/cm². Em seguida, avaliam-se os efeitos da corrosão simulada em ambiente de laboratório (corrosão acelerada) comparando-os com os efeitos da corrosão natural, utilizando para tal uma corrente variável no tempo, determinada de acordo com (11). Os parâmetros utilizados na formulação referente à formação dos produtos de corrosão, cujos dados foram extraídos de Nguyen et al. (2007), estão descritos na Tabela 1.

A discretização da malha de elementos finitos da viga de concreto armado foi feita com 2230 nós e 468 elementos triangulares para a representação da matriz de concreto, e com 952 elementos de triangulares (partículas) para a representação das armaduras. Quanto às propriedades dos materiais, o concreto possui módulo de elasticidade de 2600 kN/cm², resistência à compressão de 2.5 kN/cm², resistência à tração de 0.179 kN/cm² e coeficiente de Poisson de 0.2. Já as armaduras possuem módulo de elasticidade 21000 kN/cm² e resistência à tração de 50 kN/cm².

Nas Figura 13.a e 13.b são apresentados os resultados obtidos referentes ao deslocamento vertical e à tensão longitudinal (para três diferentes regiões da viga), considerando as solicitações químico-mecânicas (impostas pela corrosão) e as solicitações advindas do carregamento.

Observa-se na Figura 13.a que, após 50 horas de corrosão acelerada, a estrutura experimenta um acréscimo de deslocamento de 0.26 mm (para baixo) para um ponto situado na parte inferior do centro da viga (ponto “I”), enquanto que, para um ponto situado na parte superior do centro da viga (ponto “S”), o acréscimo é de 0.14 mm, quase a metade do valor observado no ponto inferior.

Figura 13. Respostas do modelo para (a) o deslocamento vertical e (b) tensão longitudinal.

Os resultados apresentados na Figura 13.b demonstram a influência da corrosão no campo de tensão da viga sob corrosão quando considerada a aplicação de um carregamento externo. Observa-se que, para o caso em que há apenas corrosão (sem carregamento), as tensões nos pontos “S” e “I” são sempre de tração (independentemente do tempo de propagação), conforme observado por Balafas e Burgoyne (2010). Entretanto, observa-se que na presença de um carregamento externo, o campo de tensão passa a ter comportamento controlado pelo nível de corrosão das armaduras. Por exemplo, o ponto “S”, situado na parte superior da viga, tem seu estado de tensão alterado de compressão para tração após 15 horas de corrosão acelerada.

Assim, verificou-se que existe uma influência significativa da corrosão nos campos de tensões de vigas de concreto armado em serviço (com carregamento). Essa influência tem efeitos secundários que corroboram com a redução da vida útil das estruturas, à exemplo, a fissuração do concreto de cobrimento. Sabe-se que o estado de fissuração de um elemento de concreto armado é altamente dependente do seu estado de tensão e, assim, se a corrosão altera o campo de tensão de um elemento estrutural, a mesma pode vir a modificar e/ou acelerar os mecanismos de ruptura do mesmo.

Na Figura 14.a é apresentada a configuração deformada da viga considerando três diferentes configurações de solicitações: (i) só corrosão; (ii) só carregamento e (iii) ação conjunta do carregamento e da corrosão. Observa-se que no caso em que as solicitações da viga são exclusivamente decorrentes da corrosão, todo o elemento estrutural está tracionado, devido à formação dos produtos de corrosão. É possível observar ainda, que os deslocamentos da viga, para o caso em que há corrosão e carregamento externo, podem ser descritos pela sobreposição das solicitações mecânicas (devido ao carregamento externo) e químico-mecânicas (decorrentes da corrosão).

Por fim, a Figura 14.b apresenta os resultados obtidos para o deslocamento vertical, da viga de concreto armado, considerando apenas a corrosão natural.

Diante dos resultados obtidos na simulação da corrosão natural, os quais são apresentados na Figura 14.b, verificou-se que o deslocamento do ponto “I”, após 50 anos de corrosão natural, é de 0.47 mm, 79% maior que o deslocamento observado após 50 horas de corrosão acelerada.

Figura 14. (a) Deslocamento vertical da viga: (a) aos 50 anos e (b) ao longo do tempo (em mm).

4. ConclusÕes

Da análise dos resultados apresentados referente à validação do modelo desenvolvido, pode-se concluir que o modelo, baseado no Método dos Elementos Finitos Posicional (MEFP), representa coerentemente a expansão do concreto devido à formação dos produtos de corrosão. Ademais, diante das simulações numéricas realizadas, foi possível concluir que:

Por último, os resultados demonstram a aplicabilidade do modelo desenvolvido como uma alternativa viável e eficiente para a simulação de elementos de concreto armado sob corrosão uniforme, colaborando com os estudos da área de patologia das construções.

5. Agradecimentos

O financiamento provido pelo Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq 141078/2018 e CNPq 310564/2018-2) é reconhecido e valorizado. O presente trabalho também foi realizado com apoio da Coordenação de Aperfeiçoamento de Pessoal de Nível Superior - Brasil (CAPES) - Código de Financiamento 001.


6. REFERÊNCIAS

Almusallam, A. A. (2001), Effect of degree of corrosion on the properties of reinforcing steel bars. Construction and Building Materials. 15(8):361-368. https://doi.org/10.1016/S0950-0618(01)00009-5

Andrade, C., Alonso, C., Molina, F. J. (1993), Cover cracking as a function of bar corrosion: Part 1 Experimental test. Materials and Structures. 26:453-464. https://doi.org/10.1007/BF02472805

Balafas, I., Burgoyne, C. J. (2011), Modeling the structural effects of rust in concrete cover. Journal of Engineering Mechanics. Journal of Engineering Mechanics. 137(3):175-185. https://doi.org/10.1061/(ASCE)EM.1943-7889.0000215

Bhargava, K., Ghosh, A. K., Mori, Y., Ramanujam, S. (2005), Modeling of time to corrosion-induced cover cracking in reinforced concrete structures. Cement and Concrete Research. 35(11):2203-2218. https://doi.org/10.1016/j.cemconres.2005.06.007

Coda, H. B. (2018), “O método dos elementos finitos posicional: sólidos e estruturas - Não linearidade geométrica e dinâmica”. Publisher: EESC-USP, Place of publication: São Carlos, SP, p. 284. ISBN: 9788580230680

Du, X., Jin, L. (2014), Meso-scale numerical investigation on cracking of cover concrete induced by corrosion of reinforcing steel. Engineering Failure Analysis. 39:21-33. https://doi.org/10.1016/j.engfailanal.2014.01.011

Felix, E. F. (2018), “Modelagem da deformação do concreto armado devido à formação dos produtos de corrosão”. Master Thesis, Escola de Engenharia de São Carlos/USP, São Carlos.

Gentil, V. (2011), “Corrosão”. Editora LCT, 6º edição, Rio de Janeiro, Brasil, p. 376.

Graeff, A. G. (2007), “Avaliação experimental e modelagem dos efeitos estruturais da propagação da corrosão em elementos de concreto armado”. Master Thesis, Universidade Federal do Rio Grande do Sul, Porto Alegre.

Hansen, E. J., Saouma, V. E. (1999), Numerical simulation of reinforced concrete deterioration: Part 2-steel corrosion and concrete cracking. ACI Materials Journal. 96:331-338. ISSN: 0889-325X.

Helene, P. (1986), “Corrosão em armaduras para concreto armado”. PINI, São Paulo, Brasil. p. 46.

Isgor, O. B., Razaqpur, A. G. (2006), Modelling steel corrosion in concrete structures. Materials and Structures. 39(3):291-302. https://doi.org/10.1007/s11527-005-9022-7

Jiang, L., Lin, B., Cai, Y. (2000), A model for predicting carbonation of high-volume fly ash concrete. Cement and Concrete Research. 30(5):699-702. https://doi.org/10.1016/S0008-8846(00)00227-1

Kiani, K., Shodja, H. M. (2011), Prediction of the penetrated rust into the microcracks of concrete caused by reinforcement corrosion. Applied Mathematical Modelling. 35(5):2529-2543. https://doi.org/10.1016/j.apm.2010.11.039

Liu, Y., Weyers, R. E. (1998), Modeling the time-to-corrosion cracking in chloride contaminated reinforced concrete structures. Materials Journal. 95(6):675-680.

Maruya, T., Hsu, K., Takeda, H., Tangtermsirikul, S. (2003), Numerical modeling of steel corrosion in concrete structures due to chloride ion, oxygen and water movement. Journal of Advanced Concrete Technology. 1(2):147-160. https://doi.org/10.3151/jact.1.147

Mehta, P. K., Monteiro, P. J. M. (2014), “Concreto: microestrutura, propriedades e materiais”. Ibracon, São Paulo, Brasil, p. 751.

Molina, F. J., Alonso, C., Andrade, C. (1993), Cover cracking as a function of bar corrosion: Part 2-Numerical model. Materials and Structures. 26 :532-548. https://doi.org/10.1007/BF02472864

Nguyen, Q. T., Caré, S., Millard, A., Berthaud, Y. (2007), Analyse de la fissuration du béton armé en corrosion accélerée. Comptes Rendus Mecanique. 335(2): 99-104. https://doi.org/10.1016/j.crme.2007.01.005

Ožbolt, J., Oršanić, F., Balabanić, G. (2014), Modeling pullout resistance of corroded reinforcement in concrete: Coupled three-dimensional finite element model. Cement and Concrete Composites. 46:41-55. https://doi.org/10.1016/j.cemconcomp.2013.10.014

Paccola, R. R., Coda, H. B. (2016), A direct FEM approach for particulate reinforced elastic solids. Composite Structures. 45:235-251. https://doi.org/10.1016/j.compstruct.2016.01.062

Paul, S. C., Zijl, G. P. A. G. V. (2016), Chloride-induced corrosion modelling of cracked reinforced SHCC. Archives of Civil and Mechanical Engineering. 16(4):734-742. https://doi.org/10.1016/j.acme.2016.04.016

Ribeiro, D., Cunha, M., Helene, P. (2015), “Corrosão em Estruturas de Concreto Armado: Teoria, Controle e Métodos de Análise”. Elsevier Brasil, Campus, São Paulo, Brasil, p. 272.

Vanalli, L., Paccola, R. R., Coda, H. B. (2008), A simply way to introduce fibers into FEM models. Communications in Numerical Methods in Engineering. 24:585-603. https://doi.org/10.1002/cnm.983

Yuan, Y., Ji, Y. (2009), Modeling corroded section configuration of steel bar in concrete structure. Construction and Building Materials. 23(6):2461-2466. https://doi.org/10.1016/j.conbuildmat.2008.09.026

Zhu, W. (2014), “Effect of corrosion on the mechanical properties of the corroded reinforcement and the residual structural performance of the corroded beams”, Doctoral Dissertation, Institut National des Sciences Appliquées de Toulouse (INSA de Toulouse).